四次贝塞尔
今天考试怎么都算不对,好烦,下午写了个玩(也不懂对不对)
真是可怕的一天
先上公式
p
(
t
)
=
[
t
4
t
3
t
2
t
1
]
[
1
−
4
6
−
4
1
−
4
12
−
12
4
0
6
−
12
6
0
0
−
4
4
0
0
0
1
0
0
0
0
]
[
p
1
p
2
p
3
p
4
p
5
]
p(t)=\begin{bmatrix}t^4&t^3&t^2&t&1\end{bmatrix} \begin{bmatrix} 1&-4&6&-4&1\\ -4&12&-12&4&0\\ 6&-12&6&0&0\\ -4&4&0&0&0\\ 1&0&0&0&0 \end{bmatrix} \begin{bmatrix}p_1\\ p_2\\ p_3\\ p_4\\ p_5\end{bmatrix}
p
(
t
)
=
[
t
4
t
3
t
2
t
1
]
⎣
⎢
⎢
⎢
⎢
⎡
1
−
4
6
−
4
1
−
4
1
2
−
1
2
4
0
6
−
1
2
6
0
0
−
4
4
0
0
0
1
0
0
0
0
⎦
⎥
⎥
⎥
⎥
⎤
⎣
⎢
⎢
⎢
⎢
⎡
p
1
p
2
p
3
p
4
p
5
⎦
⎥
⎥
⎥
⎥
⎤
把t从0到一套,线条就出来了。
代码
工具:vs2019
库:EasyX,Eigen
关于Eigen库怎么导到vs:
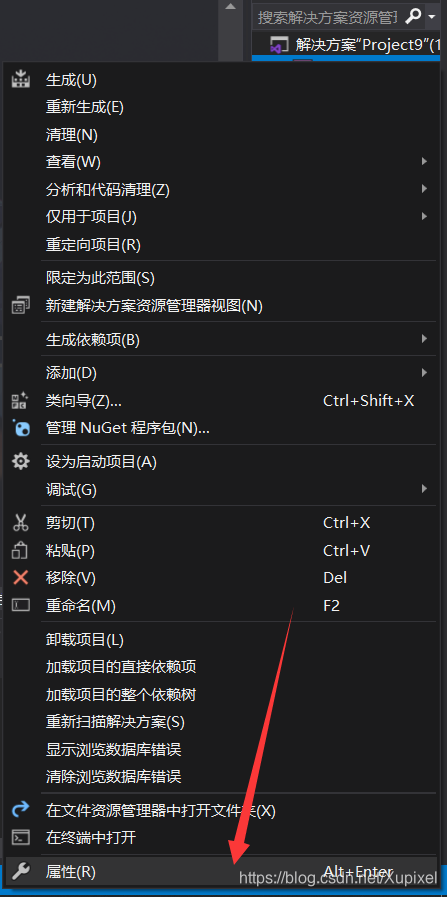
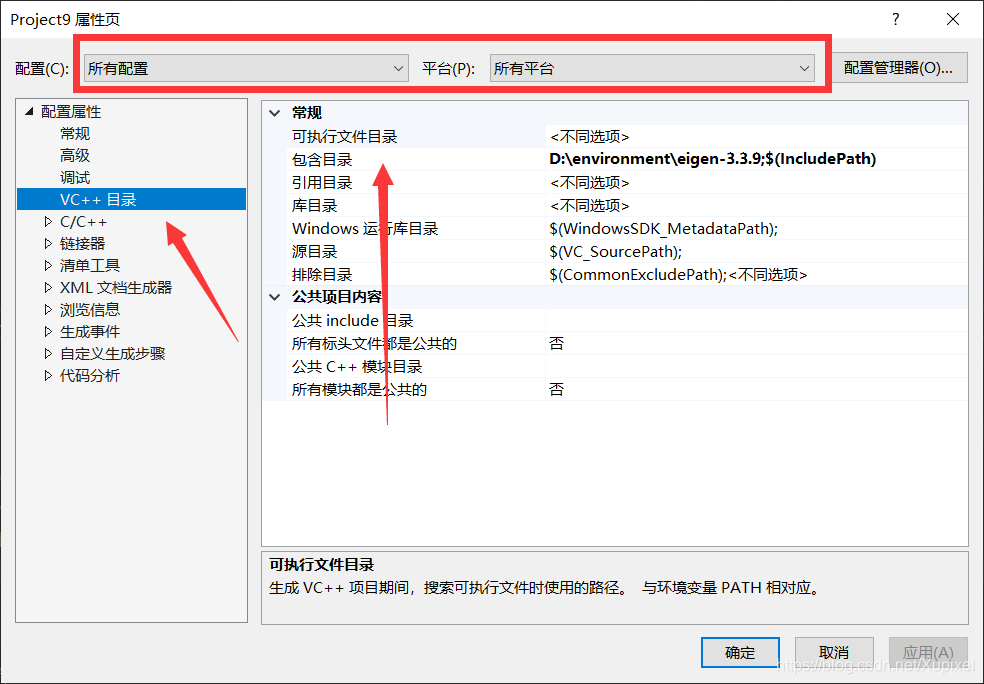

将eigen的路径添加就可以了。
//手动实现四阶贝塞尔
#include <graphics.h>
#include <conio.h>
#include <vector>
#include<Eigen/core>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
POINT pts[] = { {0,0},{100,100},{200,200},{300,300},{400,400} };
int j = -1, i;
void my_bezier(POINT pts[]) {
Matrix<double, 5, 5> M;
M << 1, -4, 6, -4, 1,
-4, 12, -12, 4, 0,
6, -12, 6, 0, 0,
-4, 4, 0, 0, 0,
1, 0, 0, 0, 0;
Matrix<double, 5, 2> B;
for (int i = 0; i < 5; i++) {
B(i, 0) = (double)pts[i].x;
B(i, 1) = (double)pts[i].y;
}
Matrix<double, 5, 2> MB = M * B;
Matrix<double, 1, 2> pre_p;
pre_p << pts[0].x, pts[0].y;
for (int i = 1; i <= 200; i++) {
double t = i / 200.0;
Matrix<double, 1, 5> T;
T << pow(t, 4), pow(t, 3), pow(t, 2), t, 1;
Matrix<double, 1, 2> p = T * MB;
line(pre_p(0, 0), pre_p(0, 1), p(0, 0), p(0, 1));
pre_p = p;
}
}
void paint() {
setcolor(DARKGRAY);
polyline(pts, 5);
setcolor(WHITE);
my_bezier(pts);
for (i = 0; i < 5; i++) {
circle(pts[i].x, pts[i].y, 10);
}
}
int main() {
initgraph(640, 480); // 初始化图形窗口
paint();
MOUSEMSG m;
while (1) {
m = GetMouseMsg();
BeginBatchDraw();
switch (m.uMsg) {
case WM_LBUTTONDOWN:
for (i = 0; i < 5; i++) {
if (abs(m.x - pts[i].x) < 10 && abs(m.y - pts[i].y) < 10)j = i;
}
case WM_MOUSEMOVE:
if (j > -1) {
pts[j] = { m.x,m.y };
cleardevice();
paint();
}
break;
case WM_LBUTTONUP:
j = -1;
break;
}
EndBatchDraw();
}
_getch(); // 按任意键退出
closegraph();
return 0;
}
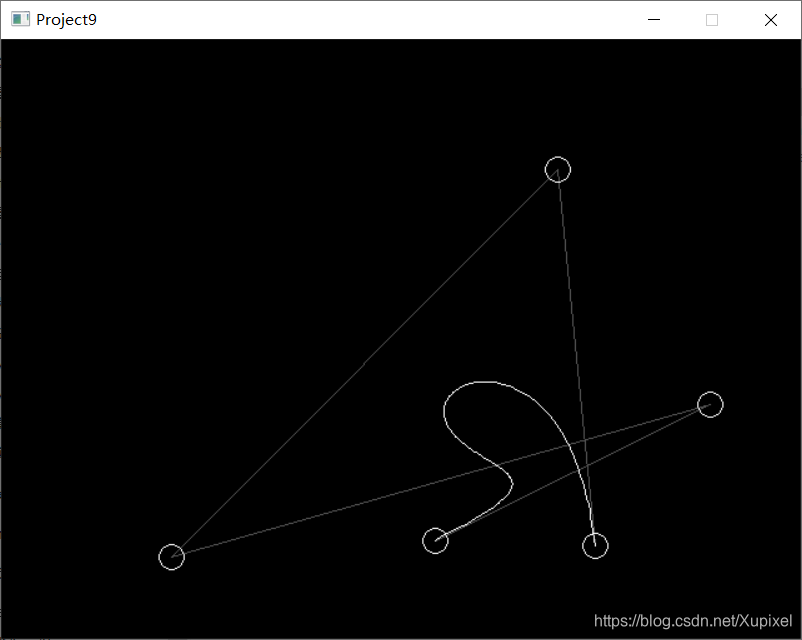
程序