博客

接对比学习（一）

L2正则使用原因

使用l2正则化的原因：

• 对比学习在做特征相似度计算时，要先对表示向量做l2正则化然后再做点积计算，或者进行cosine相似度计算。研究表明，把特征表示g(f(x))映射到单位超球面上，有这样的好处。首先，相比带有向量长度信息的点积，在去掉长度信息后的单位长度向量入如下所示的操作上，能增加深度学习模型的训练稳定性。
  
  
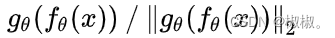
• 当把表示向量映射到球面上，如果模型的表示能力足够好，对于相似的实例会聚集到比较近的区域上，那么很容易适用线性分类器把某类与其他类别分开。将向量首先经过l2正则化后再进行相似度计算就相当于，把向量映射到了球面超面上进行相互比较。实验也表明，首先进行l2正则化能够提升模型的效果。

一个好的表示学习模型应该具备的特点：

• 一个好的对比学习应该具备以下两个属性：Alignment和Uniformity。其中，Alignment指的是相似的例子，也就是正例，映射到单位超球面后，应该具有比较接近的特征，球面距离应该比较近；Uniformity指的是系统应该倾向于应该在特征里保留尽可能多的信息，映射到球面上就要求，单位球面上的特征应该尽可能地均与分布在球面上，分布越均匀，意味着保留的特征也就越多越充分。因为，分布越均匀，意味着各自保留各自的独有的特征，这代表着信息保留越充分。

模型坍塌

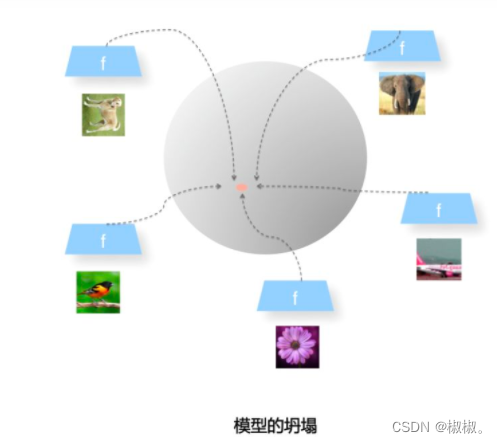
• Uniformity特性的极端反例，所有数据都映射到单位超球面的同一个点上，这代表着所有数据的信息都被丢掉，体现为数据分布极度不均匀得到了超球面上的同一个点。也就意味着，所有数据经过两次非线性计算之后都收敛到同一个常数上，这种异常情况我们称之为：模型坍塌（collapse），如上图所示。

infoNCE损失函数

• 在simCLR中，可以看到，对比学习模型结构由上下两个分支，首先会将正例对和负例对进行两次非线性计算，将训练数据映射到超球面上。然后通过提下优化目标的损失函数为infoNCE损失函数，通过损失函数来调整这些映射到单位球面上的点之间的拓扑结构关系，希望能够将正例在超球面之间的距离更为接近，负例在超球面上距离推远。infoNCE损失函数如下所示：
  
  
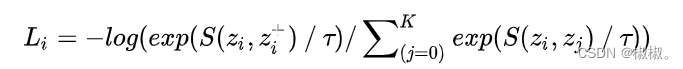
• 在公式中可知，分子中的S（）体现出了Alignment属性，它期望在超球面上正例之间的距离越近越好；分母中的S（）则体现了Uniformity属性，它期望在负例对之间的距离尽可能的远，这种水之间的推力会尽量将点尽可能地均匀分布在超球面上，保留了尽可能多的有用信息。损失函数inforNCE会在Alignment和Uniformity之间寻找折中点。如果只有Alignment模型会很快坍塌到常数，损失函数中采用负例的对比学习计算方法，主要是靠负例的Uniformity来防止模型坍塌，很多典型的对比学习方法都是基于此的。
• infoNCE的思想：正例之间相互吸引，负例之间相互排斥。
• 
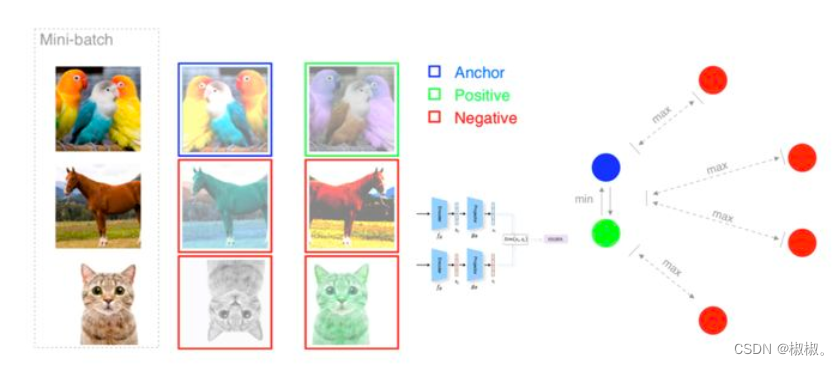
• 在infoNCE损失函数中，有一个神秘参数
  
  T
  
  ，这个参数的存在有什么用呢？很多实验研究表明，对比学习模型要想效果比较好，温度参数
  
  T
  
  需要设置一个比较小的数值，一般设置为0.1或者0.2.。infoNCE能够感知负例难度的损失函数，而之所以能够做到这一点，主要依赖与超参数
  
  T
  
  。

负例难度

• 如何感知负例的难度？什么样的负例是有难度的？

• 在对比学习中，对于数据x，除了他的唯一正例x+外，所有其他的数据都是负例。但是，这些负例有一些和x比较像，有一些差异比较大，对于比较接近原始数据特征，难以进行区分的，难度比较大；对于区别度很大，存在的共同特征表较少的，难度比较小，区分比较容易。比如：原始图像为狗，需要区分的为狗和狼，难度比较大，需要区分的为树、人，难度比较小，便于区分。

• 将其映射到超球面上就是，比较像的、有难度的负例在超球面上距离比较近，比较容易区分的在超球面上距离比较远。也就是说，距离越近的负例越难区分，距离越远的负例越容易区分。

• 

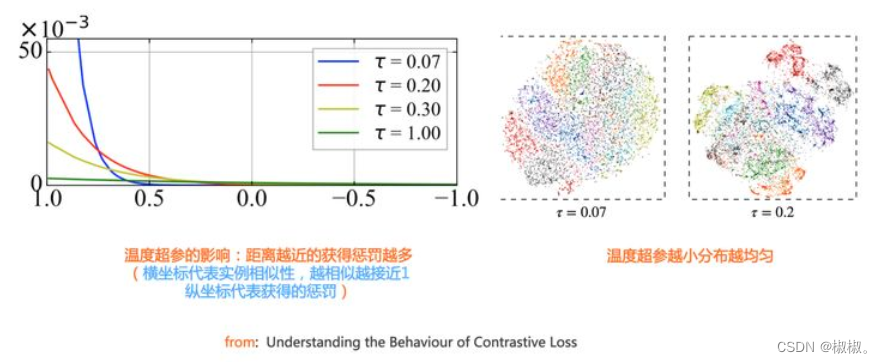
• 总而言之，温度参数T起到的作用：温度参数会将模型更新的重点，聚焦到有难度的负例，并对他们做相应的惩罚，难度越大，也即与x越接近，分配到的惩罚系数越多。所谓惩罚就是，就是在模型优化的过程中，需要将这些负例从x身上推开明时期的距离越远，是一种斥力。也就是，距离越近的负例护肤易更多的权重，会具有更大的斥力，需要将其推开的力越大。

• 如果温度超参数设置过小，会导致损失函数分配的惩罚项范围越窄，更加聚焦在比较近的范围之内负例之中。同时，如果这些被覆盖的负例，因为数量减少了，会导致分配到的每个负例上的权重更大，斥力会更大。在极端的情况下，如果温度系数接近于0，会导致infoNCE退化为Triplet（facenet人脸识别中的损失函数）。一般情况下，有效的负例智慧聚焦在距离最近的一到两个最难的实例。从上述分析可知：温度参数越小，那么超球面上的密集数据将会被打散，数据将会越来越均匀。

• 但是，温度参数也不是越小越好。由于在进行数据学习时，我们使用的是无监督，负例中有可能会存在一些潜在的正例，如果参数太小会导致比较近的潜在正例被推开，这样是不正确的。
  
  因此，我们希望能够在温度参数能够在alginment和unifoemity之间找一个平衡点。