写这篇文章的原因是基本没有关于中文大脑互补学习系统(complementary learning systems)的文章。应该说有很多关于互补学习系统的英文论文,这里也是一个总结加一点自己的见解,具体见参考文献。
海马体在学习和记忆中的角色
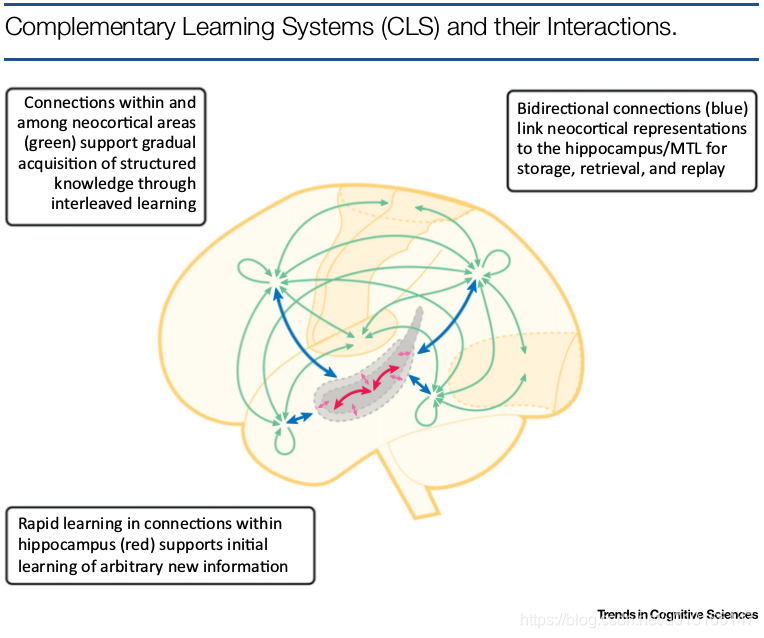
海马体系统是一个广泛存在于哺乳动物的脑区,在学习和记忆中扮演重要的特殊角色。要确切的定义海马系统的边界是困难的,这里也不去定义。应该说海马体所扮演的角色是很多重的,如下:
记忆
,
记忆是海马体的基础功能,也是所有智能生命存在的基础
,比如我们平时记忆电话号码,记忆单词,学习开车,会用到海马体,海马体不断的记忆关联事件,并且遗忘不重要的信息。尤其大家体会比较深的是记忆单词,如果几天不复习的话就忘记了,尤其是死记硬背的东西很容易遗忘,因为海马体打分机制,这种死记硬背没有与以前信息有多少关联就很容易消失了,而对于某些单词我们不但记忆他的意思还看他的用法及在很多句子中的使用,那么这种记住的单词就不容易忘记且更容易转化为长期记忆。
导航作用
,即通过存储的位置记忆碎片,重构出在当前位置下的地理空间地图(这里叫模式补全,Pattern Completion),比如:我们到了一个陌生的地方,我们就在不断的熟悉该地方的图像和感知数据,如这里是否有标志性建筑,是否有河等等,当我们迷路的时候如果回到以前到过的地方,那么海马体就可以记忆重现,给出一种到过的感觉,甚至可以通过记忆碎片重构出该地区的3D地图,然后不断的感知重放重构达到导航的目的,在计算机视觉中对应的技术为SLAM(simultaneous localization and mapping),但是现在的SLAM没有人的那么强大。
记忆检索与重构
,上面也说了扮演GPS的角色本身就有记忆检索的作用,就是根据当前看到的场景检索出相关的其他事物,而且这种检索很强大,他强大的地方在于可以通过不完整的感知数据检索出以前有过的相关事物,比如我们看到一个人的背影,那么这个背影是不完全的,但是如果这个背影是我们熟悉的人,那么我们就会产生熟悉的感觉,并且会自动的重构出这个人的其他信息,然后去识别,当然识别可能会不准确,因为相似的背影总是存在的,这个时候我们的认知系统会要求补充信息(主动信息收集),如一个人的正面,这个时候就可以达到非常准确的辨别。
信息整合
,上面的两个作用应该也阐述出了信息整合的功能,对于不完整的信息,比如我们在大街上看见一个熟悉的面孔,但是这个时候我们的认知系统不会马上判断这个人,而是先判断这个人可能是谁,再去整合出预测的人平时的信息,包括发型,穿什么样的衣服,穿什么样的鞋子,走路姿态,甚至声音…然后再根据整合的信息与当前这个人的信息加权对比,然后再去判断这个人是谁,当然整合的信息可以不是所有信息,只要当前有效信息达到可靠的预测精度就可以了。可以看到我们判断人更多的是依靠综合的上下文信息,不断检索出事件相应的信息,最后根据检索出的信息作判断,甚至当检索信息仍然不足以判断的时候认知系统还要求主动的收集必要的信息到海马体,如:我们看警察侦查案件的时候,信息往往是不充分的,这个时候信息搜集就是必要的。上面我们也看到了信息整合包含了重建上下文信息的作用,自动关联与记忆检索本身就在重建上下文信息,如看到词汇:医院,就能相应的重建出医生,护士,生病,开刀等等上下文信息。这里的上下文和神经网络模型 RNN,LSTM,NTM所利用的上下文有很大不同。
自动关联
,应该说海马体无时无刻不在自动关联相应的信息,比如我们听歌的时候会关联到当时的心里状态,外部环境,只是说这种关联可能变成了长期的关联,我们有的时候会听到以前听过的歌的时候,会重现出当时的心情。其实这些关联都是潜意识的,有的时候我们并没有意识到,而这种能力或许是无监督学习的关键。
快速学习
,如我们学习打街机游戏,刚开始的时候是不会的,这个时候我们就需要记住在某个状态时应该做哪个操作,即成对的输入-输出映射 input-output pairs mapping,然后不断的这样做,这个时候实际上我们并没有学会,而只是根据状态给出操作,而且反应并不快,这种快速的学习能力和记忆有点类似。
辅助学习
,海马体有记忆的作用,而这种记忆可能是很容易消失的,比如我们学习开车这种重复性很高的技能,那么海马体是如何做的呢?即将记忆转化为技能,而这种转化过程叫学习。应该说这种转化过程是无时无刻不在进行的,只是我们很难意识到,尤其在睡眠期间的记忆重放,那么你是否有在第二天感觉到技能提升呢?这就是海马体辅助新皮层学习,即将关联记忆重放出来使新皮层学习为潜意识的条件反射。这种辅助学习可能是一种权衡机制,如果本身海马体就可以处理当前问题为什么要转化为类似于条件反射的的技能呢?可能是计算复杂度的权衡,如果每时每刻都要海马体去检索当前状态所应该的操作是很耗能量的,所以如果把这种(状态,操作)的成对事件学习为直接映射那么就能达到更快的速度和更少的能量消耗。还有就是海马体的记忆容量是有限的,这么多的成对数据如果转化学习为映射函数那么就能获得更紧凑的表示。
新皮层系统
新皮层占据成年人整个大脑皮层表面的94%,相对于海马体,新皮层显得更为简洁。新皮层的功能是非常多的,如:把声音转成语言、处理颜色、表达恐惧、辨识面孔、物体识别等等,新皮层的简洁在于每个区都有特定的功能,如辨识,语言等,都在各自的分区内,而海马体是一个相对比较混合的系统。相对于海马体,新皮层的学习速度很慢,比如我们学习骑车,尤其是刚学习的时候,当然这个时候海马体是参与进来了的,理论上说,当我们不再依赖注意力去学习的时候才算新皮层学会了骑车。而在学习的过程中又牵涉到灾难性遗忘(Catastrophic forgetting)与增量学习问题[8-9],比如如果我们用学习开车的这个区域再去学习跳舞,那么就会导致该区域学习开车的技能丢失,那么我们也知道,
我们大脑是采取用分区来避免这个差异性比较大的学习造成灾难干扰
。
用人工神经网络来说就是,这两个任务或许有相似的结构但是他们的参数是很不同的,两个任务序列学习会导致前面任务的遗忘。
而如骑自行车和骑摩托车是相似的任务,而且往往现实中相似任务是非常多的,如果我们全都用不同的脑区去学习就很浪费脑空间,所以这里就有一个机制来权衡网络的结构和参数,最大化参数和结构的利用,使得相似的任务有相似的激活脑区域。
其他
结构是智能生命的核心,深有感悟
“Structure is always central in biology,” said study leader Scott Emmons, Ph.D., professor of genetics and in the Dominick P. Purpura Department of Neuroscience and the Siegfried Ullmann Chair in Molecular Genetics at Einstein. “The structure of DNA revealed how genes work, and the structure of proteins revealed how enzymes function. Now, the structure of the nervous system is revealing how animals behave and how neural connections go wrong to cause disease.”
总结
互补学习系统是一个大脑学习的重要框架,权衡了快速学习和慢速学习,快速学习与慢速学习都有各自的优点和缺陷,快速学习学习速度快但是更加消耗时间与能量,快学习也在为慢学习准备数据,而慢速学习学习速度慢但是可以利用结构和参数信息紧凑的表示任务,且在新皮层工作的时候有快的运行速度,慢学习更像是用空间换时间,这就解释了为什么我们的新皮层很大,因为要容纳非常多的任务,相对而言海马体就小了很多能容纳的任务就很少,现在的神经网络也类似与新皮层系统,也会产生灾难性遗忘,那么如何避免灾难性遗忘与增量学习,需要借鉴于我们大脑的处理方式。
参考:
1. Complementary Learning Systems
2. Conjunctive Representations inLearning and Memory:Principles of Cortical andHippocampal Function
3. Hippocampal and neocortical contributions to memory: advances in the complementary learning systems framework
4. Hippocampus, cortex, and basal ganglia: Insightsfrom computational models of complementary learning systems
5. Modeling Hippocampal and Neocortical Contributionsto Recognition Memory: A Complementary LearningSystems Approach
7. Multiple View Geometry in Computer Vision
8. Catastrophic Forgetting in Connectionist Networks
9. Overcoming catastrophic forgetting in neural networks
10.
What Learning Systems do Intelligent Agents Need? Complementary Learning Systems Theory Updated
如有错误请不吝指出