非线性规划

非线性规划的最优解可能在可行域的任何地方取得。
一元函数:二阶导数>=0,曲线凹,即下凸。
二元函数:图解法

凸集:
集合中任意取两个点x1和x2,若x1和x2之间的任意一个点都在该集合中
,则该集合为凸集。

凸规划
凸规划:可行域是凸集,函数是凸函数。

求f(x)的H矩阵,H矩阵一定是对称矩阵(除了主对角线以外,其余元素关于主对角线对称)。
若H矩阵半正定,则f(x)是凸集上的凸函数;若为正定,则为严格凸函数。
判单正定或半正定或 不定的方法:
求对称矩阵的顺序主子式(各阶取同行同列,如:一阶取一行一列,二阶取1,2行,1,2列)
若所有行列式严格>0,则说明是正定的;
若>=0,则有可能是半正定,则计算主子式。主子式:一阶取第一行一列,二阶任取两行两列。
若主子式>0,则说明是半正定。
若所有计算过程中,出现行列式<0的情况,则为不定。
二次规划

无约束最优化方法
如何找到唯一的极小值点?
一元函数(一维搜索)
先求出驻点,判断是不是极值点,否则则用以下方法。
- 黄金分割法(找到单谷区间(驻点的可能区间),0.618法)
- 牛顿法
牛顿法详解



两种方法可同时使用。
梯度:偏导数构成的列向量。可写为:长度**单位向量(也就是步长*方向)
多元函数:
- 最速下降法(梯度法)

这一步可看为一维搜索,即求t使得f最小。
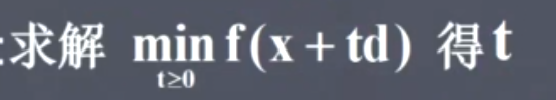
-
牛顿法

步骤

约束最优化方法
(把非线性规划转换为线性规划)
- 只有等式约束:构造拉格朗日函数(条件极值)
- 只有不等式约束:障碍函数法
-
二者都有:惩罚函数法
构造增广目标函数=目标函数+惩罚函数
罚函数法(外部惩罚法)
障碍函数法(内部惩罚法)
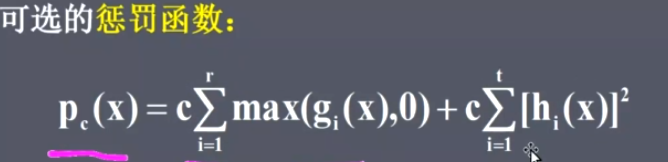
只要x不在可行域里,函数值不会等于0,c是很大的常数,所以p(x)会很大,也就是惩罚很大。