1、0-1背包问题
0-1背包问题
:有一个贼在偷窃一家商店时,发现有n件物品,第i件物品价值v
i
元,重w
i
磅,此处v
i
与w
i
都是整数。他希望带走的东西越值钱越好,但他的背包中至多只能装下W磅的东西,W为一整数。应该带走哪几样东西?这个问题之所以称为0-1背包,是因为每件物品或被带走;或被留下;小偷不能只带走某个物品的一部分或带走同一物品两次。
注:在选择装入背包的物品时,对每种物品i只有2种选择,即装入背包或不装入背包。不能将物品i装入背包多次,也不能只装入部分的物品i。(比如玉器,花瓶等)
在(分数(部分))
背包问题(fractional knapsack problem)
中,场景与上面问题一样,但是窃贼可以带走物品的一部分,而不必做出0-1的二分选择。可以把0-1背包问题的一件物品想象成一个金锭,而部分问题中的一件物品则更像金沙。
2、贪心算法(按单位重量价值排序)(含为什么不可以解决)
首先声明:虽然两个问题相似,但我们
可以用贪心策略可以求解背包问题,而不能求解0-1背包问题
,为了求解部分数背包问题,我们首先计算每个商品的每磅价值v
i
/w
i。遵循贪心策略,小偷首先尽量多地拿走每磅价值最高的商品,如果该商品已全部拿走而背包未装满,他继续尽量多地拿走每磅价值第二高的商品,依次类推,直到达到重量上限W。因此,通过将商品按每磅价值排序,贪心算法的时间运行时间是O(nlgn)。
对于这个问题,一开始确实有点不太好入手。一堆的物品,每一个都有一定的质量和价值,我们能够装入的总重量有限制,该怎么来装使得价值最大呢?对于这n个物品,每个物品我们可能会选,也可能不选,那么我们总共就可能有2^n种组合选择方式。如果我们采用这种办法来硬算的话,则整体的时间复杂度就达到指数级别的,肯定不可行。
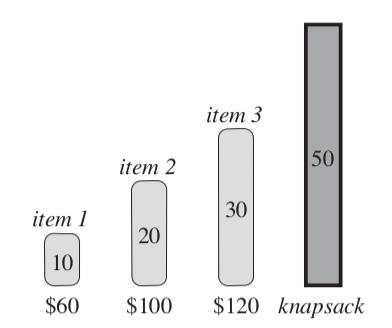
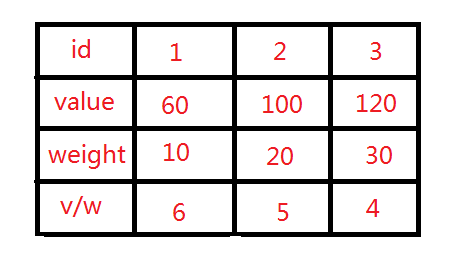
现在我们换一种思路。既然每一种物品都有价格和重量,我们优先挑选那些单位价格最高的是否可行呢?比如在下图中,我们有3种物品,他们的重量和价格分别是10, 20, 30 kg和60, 100, 120。
那么按照单位价格来算的话,我们最先应该挑选的是价格为60的元素,选择它之后,背包还剩下50 – 10 = 40kg。再继续前面的选择,我们应该挑选价格为100的元素,这样背包里的总价值为60 + 100 = 160。所占用的重量为30, 剩下20kg。因为后面需要挑选的物品为30kg已经超出背包的容量了。我们按照这种思路能选择到的最多就是前面两个物品。如下图:

按照我们前面的期望,这样选择得到的价值应该是最大的。可是由于有一个背包重量的限制,这里只用了30kg,还有剩下20kg浪费了。这会是最优的选择吗?我们看看所有的选择情况:

很遗憾,在这几种选择情况中,我们前面的选择反而是带来价值最低的。而选择重量分别为20kg和30kg的物品带来了最大的价值。看来,我们刚才这种选择最佳单位价格的方式也行不通。
网上基本上证明“贪心算法不能解决0-1背包问题“都是采用上面的例子,但是我起初在想可不可以在”按照单位重量价值“排序以后,从每个点都开始一次贪心遍历呢?比如上例,从10 走一趟,再从20走一趟。。。。。。
天真了!主要是被上面例子迷惑了。。。。。
看这个例子:背包可承受100
id …… 5 6 7 8 9……. 20
v/w
5 6 7 8 9
1000000
W 20 20 20 20 20 80
在上面例子中,按贪心计算的话是选择5,6,7,8,9,,但是明显可以看出应该选5,20。也就是贪心算法无法从“当前全局”去决策!比如从5号开始,遍历到9号,已经背包满了,再往后遍历,即使有最优解也无法剔除前面已经装进去的。。。
最重要的原因是下面这条:
对于0-1背包问题,贪心选择之所以不能得到最优解是因为:
它无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了
。
事实上,在考虑0-1背包问题时,应比较选择该物品和不选择该物品所导致的最终方案,然后再作出最好选择。由此就导出许多互相重叠的子问题。这正是该问题可用动态规划算法求解的另一重要特征。
3、动态规划
f[i][v]:表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。
状态转移方程是:f[i][v]=max{f[i-1][v],f[i-1][v-weight[i]]+value[i]} //
这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来的。
解释一下上面的方程:“将前i件物品放入容量为v的背包中”这个子问题,如果只考虑第i件物品放或者不放,那么就可以转化为只涉及前i-1件物品的问题:
即1、如果不放第i件物品,则问题转化为“
前i-1件物品
放入容量为v的背包中”;
2、如果放第i件物品,则问题转化为“
前i-1件物品
放入剩下的容量为v-weight[i]的背包中”,此时能获得的最大价值就是f [i-1][v-weight[i]]再加上通过放入第i件物品获得的价值value[i]。
则f[i][v]的值就是1、2中最大的那个值。
// 背包问题
#include <iostream>
#include <algorithm>
using namespace std;
#define N 3 // N件宝贝
#define C 5 // C是背包的总capacity
int main()
{
int value[N + 1] = { 0, 60, 100, 120 }; // 价值
int weight[N + 1] = { 0, 1, 2, 3 }; // 重量
int f[N + 1][C + 1] = { 0 }; // f[i][j]表示在背包容量为j的情况下,前i件宝贝的最大价值
int i = 1;
int j = 1;
for (i = 1; i <= N; i++) //外循环控制物品数量,确保每个物品都会被遍历到
{
/*for (j = weight[i]; j <= C; j++) //内循环控制物品的重量,确保能够遍历出“以前每个物品放入时的最大价值f[i][j]”
{
int x = f[i - 1][j]; //不放第i件物品
int y = f[i - 1][j - weight[i]] + value[i]; //放入第i件物品
f[i][j] = max(x, y);
}*/
for (j = 1; j <= C; j++)
{
// 递推关系式
if (j < weight[i])
{
f[i][j] = f[i - 1][j];
}
else
{
int x = f[i - 1][j];
int y = f[i - 1][j - weight[i]] + value[i];
f[i][j] = max(x, y);
}
}
}
for (i = 0; i <= N; i++)
{
for (j = 0; j <= C; j++)
{
printf("%4d ", f[i][j]);
}
cout << endl;
}
cout << endl << "选取的最大价值是:" << f[N][C] << endl;
cout << "选取的物品如下:" << endl;
i = N, j = C;
while (i)
{
if (f[i][j] == (f[i - 1][j - weight[i]] + value[i]))
{
cout << i << ":" << "weight=" << weight[i] << ", value=" << value[i] << endl;
j -= weight[i];
}
i--;
}
cout << endl;
return 0;
}
运行结果:
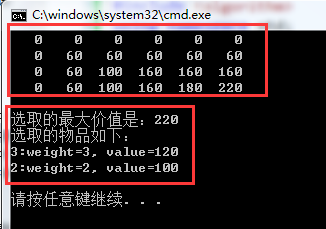
如果把上面代码中内循环改成注释部分,则运行结果如下:(个人认为写成注释部分的代码,更容易理解)
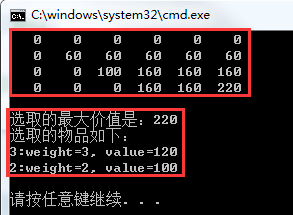
以上方法的时间和空间复杂度均为O(N*V),其中时间复杂度基本已经不能再优化了,但空间复杂度却可以优化到O(V)。
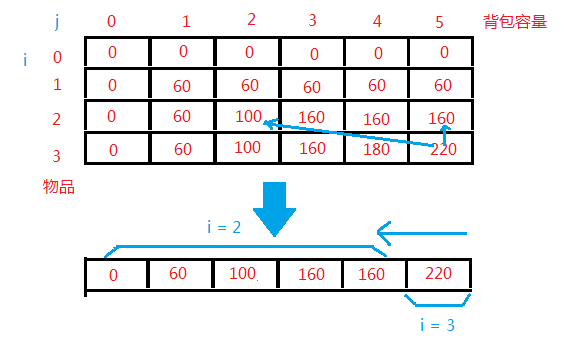
结合上面的例子,有三件物品,背包的最大负重量是5,求可以取得的最大价值。为了方面说明,物品weight依次为:1,2,3。二维数组下的求解顺序,物品数1—>n, 背包容量1—>w。如图,要使用一维数组,背包容量要采用倒序,即w—>1, 只有这样对于方程 dp( j ) = Max( dp( j ), dp (j-w[i] ) + v[i] ),才能达到等式左边才表示i,而等式右边表示i-1的效果。
优化空间复杂度:
上面f[i][v]使用二维数组存储的,可以优化为一维数组f[v],将主循环改为:
for i = 1..N;
for v = V..0;
f[v] = max(f[v], f[v-c[i]]+w[i]);
即
将第二层循环改为从V..0,
逆序
。
解释一下:
假设最大容量M=10,物品个数N=3,物品大小weight{3,4,5},物品价值value{4,5,6}。
当进行第i次循环时,f[v]中保存的是上次循环产生的结果
,即第i-1次循环的结果(i>=1)。
所以
f[v] = max { f[v],f[v-c[i]]+w[i] }
这个式子中,等号右边的f[v]和f[v-c[i]]+w[i]都是前一次循环产生的值。
f[0..10]初始值都为0。所以
:
当i=1时:
f[10]=max{f[10],f[10-weight[1]]+value[1]}=max{0,f[7]+4}=max{0,0+4}=4;
f[9]=max{f[9],f[9-
weight
[1]]+
value
[1]}=max{0,f[6]+4}=max{0,0+4}=4;
……
f[3]=max{f[3],f[3-
weight
[1]]+
value
[1]}=max{0,f[3]+4}=max{0,0+4}=4;
f[2]=max{f[2],f[2-
weight
[1]]+
value
[1]}=max{0,f[2-3]+4}=0;//数组越界?
f[1]=0;
f[0]=0;
当i=2时,此时f[0..10]经过上次循环后,都已经被重新赋值,即f[0..2]=0,f[3..10]=4。利用f[v]=max{f[v],f[v-
weight
[i]]+value[i]}这个公式计算i=2时的f[0..10]的值。
具体的值如下表所示:

因此,利用逆序循环就可以保证在计算f[v]时,公式 f[v]=max{f[v],f[v-
weight
[i]]+value[i]} 中
等号右边的 f[v] 和 f[v-weight[i]]+value[i] 保存的是 f[i-1][v] 和 f[i -1][v-weight[i]] 的值
。
当i=N时,得到的f[
weight
]即为要求的最优值。
#include <iostream>
#include <vector>
using namespace std;
const int MIN = 0x80000000;
const int N = 3; //物品数量
const int V = 5; //背包容量
int f[V + 1]; // 一维数组
int Package(int *W, int *C, int N, int V)
{
int i, j;
memset(f, 0, sizeof(f)); //初始化为0
for (i = 1; i <= V; i++) //此步骤是解决是否恰好满足背包容量,
f[i] = MIN; // 若“恰好”满足背包容量,即正好装满背包,则加上此步骤; 若不需要“恰好”,则初始化为0
for (i = 1; i <= N; i++)
for (j = V; j >= C[i]; j--) //注意此处与解法一是顺序不同的,弄清原因
{
f[j] = (f[j]>f[j - C[i]] + W[i]) ? f[j] : (f[j - C[i]] + W[i]);
cout << "f[" << i << "][" << j << "]=" << f[j] << endl;
}
return f[V];
}
void main()
{
int W[4] = { 0, 7, 5, 8 }; //物品权重
int C[4] = { 0, 2, 3, 4 }; //物品大小
int result = Package(W, C, N, V);
if (result > 0)
{
cout << endl;
cout << "the opt value:" << result << endl;
}
else
cout << "can not find the opt value" << endl; // 可能不存在正好装满背包的解
}
在求最优解的背包问题中,一般有两种不同的问法:
1、要求“恰好装满背包”时的最优解:
在初始化时除了 f[0] 为
0
其它f[1..V]均设为
-∞
,这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。如果不能恰好满足背包容量,即不能得到 f[V] 的最优值,则此时 f[V] =-∞,这样就能表示没有找到恰好满足背包容量的最优值。
2、求小于等于背包容量的最优解,即不一定恰好装满背包:
如果并没有要求必须把背包装满,而是只希望价值尽量大,初始化时应该将f[0..V]全部设为
0
。
很多内容来自:
http://www.cnblogs.com/fly1988happy/archive/2011/12/13/2285377.html
http://blog.csdn.net/sj13051180/article/details/6687674