一、算法简介
1、贝塞尔曲线于1962年由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。
2、贝塞尔曲线是应用于二维图形应用程序的数学曲线,由一组称为控制点的向量来确定,给定的控制点按顺序连接构成控制多边形,贝塞尔曲线逼近这个多边形,进而通过调整控制点坐标改变曲线的形状。
二、算法思想
1、对于车辆系统,规划的轨迹应满足以下准则:轨迹连续;轨迹曲率连续; 轨迹容易被车辆跟随,且容易生成。
2、给定n+1个数据点,p0~pn,生成一条曲线,使得该曲线与这些点描述的形状相符。



三、算法推导
1、设P0,P1两个控制点,t取值范围为[0,1]。则贝塞尔曲线生成点可以表达为:
![]()

2、针对P0,P1,P2三个控制点,t取值范围为[0,1]。P0和P1构成一阶,P1和P2也构成一阶,即:

在生成的两个一阶点基础上,可以生成二阶贝塞尔点:
![]()

设P0,P1,P2,P3个控制点,P0和P1、P1和P2、P2和P3都构成一阶,即:
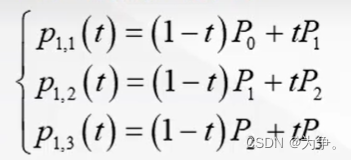
在生成的三个一阶点基础上,可以生成两个二阶贝塞尔点:

在生成的两个二阶点基础上,可以生成三阶贝塞尔点:

针对P0,P1,P2三个控制点而言,由以下三个递推式得到贝塞尔点:

则贝塞尔点与3个控制点的关系为:

二阶贝塞尔曲线 最多一阶导数不为常数。
3、针对P0、P1、P2、P3四个控制点而言,由一下三个递推式得到贝塞尔点

则贝塞尔点与四个控制点的关系为:

最多二阶导数不为常数
4、对于PO,P1,P2,….,Pn共n+1个控制点而言,贝塞尔点定义为:





% 贝塞尔曲线法:直观动图感受贝塞尔曲线行程过程
% 作者:Ally
% 日期:2021/1/30
clc
clear
close all
%% 直观动图感受贝塞尔曲线行程过程
% 一次贝塞尔曲线
P0 = [0, 0];
P1 = [1, 1];
P = [P0; P1];
figure;
plot(P(:,1), P(:,2), 'k');
MakeGif('一次贝塞尔曲线.gif',1);
hold on
for t = 0:0.01:1
P_t = (1-t)*P0 + t*P1;
scatter(P_t(1), P_t(2), 200, '.r');
stringName = "一次贝塞尔曲线:t =" + num2str(t);
title(stringName)
MakeGif('一次贝塞尔曲线.gif',t*100+1);
end
% 二次贝塞尔曲线
P0 = [0, 0];
P1 = [1, 1];
P2 = [2, 1];
P = [P0; P1; P2];
figure;
plot(P(:,1), P(:,2), 'k');
MakeGif('二次贝塞尔曲线.gif',1);
hold on
scatter(P(:,1), P(:,2), 200, '.b');
for t = 0:0.01:1
P_t_1 = (1-t)*P0 + t*P1;
P_t_2 = (1-t)*P1 + t*P2;
P_t_3 = (1-t)*P_t_1 + t*P_t_2;
h1 = scatter(P_t_1(1), P_t_1(2), 300, '.g');
h2 = scatter(P_t_2(1), P_t_2(2), 300, '.g');
h3 = plot([P_t_1(1), P_t_2(1)], [P_t_1(2), P_t_2(2)], 'g', 'linewidth',2);
scatter(P_t_3(1), P_t_3(2), 300, '.r');
stringName = "二次贝塞尔曲线:t =" + num2str(t);
title(stringName)
MakeGif('二次贝塞尔曲线.gif',t*100+1);
delete(h1);
delete(h2);
delete(h3);
end
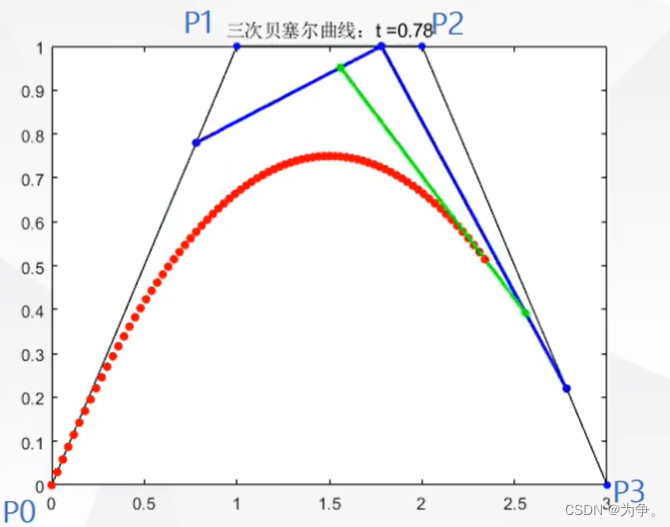
% 三次贝塞尔曲线
P0 = [0, 0];
P1 = [1, 1];
P2 = [2, 1];
P3 = [3, 0];
P = [P0; P1; P2; P3];
figure;
plot(P(:,1), P(:,2), 'k');
MakeGif('三次贝塞尔曲线.gif',1);
hold on
scatter(P(:,1), P(:,2), 200, '.b');
for t = 0:0.01:1
P_t_1_1 = (1-t)*P0 + t*P1;
P_t_1_2 = (1-t)*P1 + t*P2;
P_t_1_3 = (1-t)*P2 + t*P3;
P_t_2_1 = (1-t)*P_t_1_1 + t*P_t_1_2;
P_t_2_2 = (1-t)*P_t_1_2 + t*P_t_1_3;
P_t_3 = (1-t)*P_t_2_1 + t*P_t_2_2;
h1 = scatter(P_t_1_1(1), P_t_1_1(2), 300, '.b');
h2 = scatter(P_t_1_2(1), P_t_1_2(2), 300, '.b');
h3 = scatter(P_t_1_3(1), P_t_1_3(2), 300, '.b');
h4 = plot([P_t_1_1(1); P_t_1_2(1)], [P_t_1_1(2); P_t_1_2(2)], 'b', 'linewidth',2);
h5 = plot([P_t_1_2(1); P_t_1_3(1)], [P_t_1_2(2); P_t_1_3(2)], 'b', 'linewidth',2);
h6 = scatter(P_t_2_1(1), P_t_2_1(2), 300, '.g');
h7 = scatter(P_t_2_2(1), P_t_2_2(2), 300, '.g');
h8 = plot([P_t_2_1(1); P_t_2_2(1)], [P_t_2_1(2); P_t_2_2(2)], 'g', 'linewidth',2);
scatter(P_t_3(1), P_t_3(2), 300, '.r');
stringName = "三次贝塞尔曲线:t =" + num2str(t);
title(stringName)
MakeGif('三次贝塞尔曲线.gif',t*100+1);
delete(h1);
delete(h2);
delete(h3);
delete(h4);
delete(h5);
delete(h6);
delete(h7);
delete(h8);
end
% 贝塞尔曲线法:基于贝塞尔曲线规划换道轨迹
% 作者:Ally
% 日期:2021/1/30
clc
clear
close all
%%
% 定义控制点
d = 3.5;
P0 = [0, -d/2];
P1 = [25, -d/2];
P2 = [25, d/2];
P3 = [50, d/2];
P = [P0; P1; P2; P3];
% 直接根据贝塞尔曲线定义式得到路径点
n = length(P)-1;
Path = [];
for t = 0:0.01:1
if n == 1
p_t = P;
elseif n >= 2
p_t = [0, 0];
for i = 0:n
k_C = factorial(n) / (factorial(i) * factorial(n-i));
k_t = (1-t)^(n-i) * t^i;
p_t = p_t + k_C * k_t * P(i+1,:);
end
Path(end+1,:) = p_t;
else
disp('控制点输入有误,请重新输入')
end
end
%% 画图
d = 3.5; % 道路标准宽度
W = 1.8; % 汽车宽度
L = 4.7; % 车长
figure
len_line = 50;
% 画灰色路面图
GreyZone = [-5,-d-0.5; -5,d+0.5; len_line,d+0.5; len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0.5 0.5 0.5]);
hold on
fill([P0(1),P0(1),P0(1)-L,P0(1)-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'b')
% 画分界线
plot([-5, len_line],[0, 0], 'w--', 'linewidth',2); %分界线
plot([-5,len_line],[d,d],'w','linewidth',2); %左边界线
plot([-5,len_line],[-d,-d],'w','linewidth',2); %左边界线
% 设置坐标轴显示范围
axis equal
set(gca, 'XLim',[-5 len_line]);
set(gca, 'YLim',[-4 4]);
% 绘制路径
scatter(P(:,1),P(:,2),'g')
plot(P(:,1),P(:,2),'r');%路径点
scatter(Path(:,1),Path(:,2),200, '.b');%路径点
function MakeGif(filename,index)
f = getframe(gcf);
imind = frame2im(f);
[imind,cm] = rgb2ind(imind,256);
if index==1
imwrite(imind,cm,filename,'gif', 'Loopcount',inf,'DelayTime',0.001);
else
imwrite(imind,cm,filename,'gif','WriteMode','append','DelayTime',0.001);
end
end 学习自B站:小黎的Ally