matlab基本操作与矩阵运算
基本操作
把matlab当作计算器使用
把matlab当计算器使用基本符合常识,不过多赘述(下同,着重记录与常识有出入的地方)。
需要注意的有:
-
=
表示赋值,判断是否相等用
==
; -
matlab中没有
ln( )
函数,
log( )
默认以
e
为底; -
matlab中要表示自然对数
e
,用
exp(1)
表示即可;表示以
e
为底数的指数函数用
exp(n)
(e的n次方)
变量
- 与一般语言不同,matlab对于变量可以直接使用,不需要提前声明;
- matlab变量大小写敏感;
- matlab中变量命名规则与c一致;
-
matlab已有的保留变量不适合做变量名,调用
iskeyword
命令查看。
课件问题:

- matlab大小写敏感,大写与小写有区别
- matlab的变量不能以数字开头
变量类型
对于matlab的变量类型可以是如下这些:

对于数值变量,不显示指明变量类型,默认double类型,就数模而言基本足够。
避免使用与函数、脚本同名的变量
若出现与函数同名的变量名,调用时优先当作变量名处理。
cos='This string.';
cos(8) % 对字符串进行索引取值,得到'r'
出现这种情况可以使用
clear
+
变量名
清除该变量,即
clear cos
便可正常使用
cos( )
函数。
顺带一提
clear
:清除workspace内所有变量(即清空存储区)
clear <name>
:清除
name
变量
clc
:清空终端窗口(变量依然存在)
格式控制
一些常用的命令:
-
紧凑显示格式:
format compact
-
宽松显示格式:
format loose
-
数据高精度显示:
format long
-
数据低精度显示:
format short
-
以分数显示:
format rat
值得一提的是,无论以分数显示还是以小数显示,其在matlab内部存储的值都是一样的。
另外需要注意:
- 如果原数值是无理数,显示的分数是在一定误差范围内的有理分式近似值
- 可以通过
R = rat(x)
将小数
x
以分数的形式赋值给
R
,
该分数实际上是一个字符串,也就是说R储存的将是一个字符串
-
在一行命令后紧接着
;
,使结果不显示在终端窗口中
一点补充
who
:显示工作区内所有的变量
whos
:显示工作区内所有变量的详细信息
whos <name>
:显示变量
name
的详细信息
矩阵运算
矩阵的定义
区分
vector
与
matrix
:
vector
指向量,
matrix
指矩阵,而
array
则是两者的统称。
,
和
空格
用来间隔列
column
,
;
用来间隔行
row
a = [1 2 3]; %这是一个行向量
b = [4, 5, 6]; %这也是一个行向量
c = [7; 8; 9]; %这是一个列向量
向量乘法
行向量乘列向量结果是一个数,而列向量乘行向量结果是一个矩阵:
>> a=[1 4 6];
>> b=[3;4;8];
>> a*b % 行向量乘列向量
ans =
67
>> b*a % 列向量乘行向量
ans =
3 12 18
4 16 24
8 32 48
矩阵索引
可以有多种索引方式,普通的
a(x, y)
即第x行,第y列;
a(n)
即从第一列开始依次1、2、3…;如图
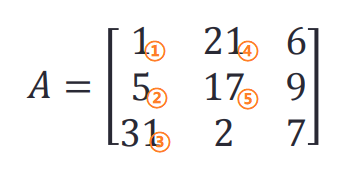
比较特殊的索引:

特别注意
A([1 3 5])
、
A([1 3; 1 3])
及
A([1 3], [1 3])
三者的区别
>> A=[1 21 6; 5 17 9; 31 2 7];
>> A([1 3 5])
ans =
1 31 17
>> A([1 3; 1 3])
ans =
1 31
1 31
>> A([1 3], [1 3])
ans =
1 6
31 7
使用
:
创建向量
:
-
x = j:k
创建一个包含元素
[j,j+1,j+2,...,j+m]
的单位间距向量 x -
x = j:i:k
创建一个
j
为起点,
k
为终点,步长为
i
的向量
str = 'a':2:'z'
将给出一个字符串:
'acdfh....z'
赋值给
str
使用
:
索引
:
使用
A(3,:)
索引矩阵
A
的整个第三行
A(3,:)=[]
使矩阵
A
的整个第三行等于空矩阵:

矩阵串联
两个行数相同的矩阵可以通过
,
或
空格
横向串联
。即
[A,B]
或
[A B]
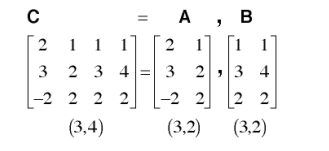
注意
A+B
并不能实现矩阵串联,而是
矩阵加法
两个列数相同的矩阵可以通过
;
纵向串联
。
F=[[A,B];C;D]
实现下图:
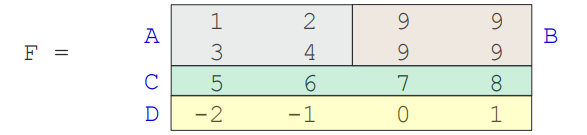
矩阵运算
- 矩阵加减运算均为对应元素的加减
-
矩阵乘除运算区分
.*
,
./
与
*
,
/
.*
为对应元素相乘,而普通的
*
则为矩阵乘法。 -
矩阵的乘方
^
与矩阵乘除法类似,
.^
为对应元素的乘方。 -
矩阵转置
'
,即为现代中的转置。
% 转置的一点运用
>> M=rand(4)
M =
0.8147 0.6324 0.9575 0.9572
0.9058 0.0975 0.9649 0.4854
0.1270 0.2785 0.1576 0.8003
0.9134 0.5469 0.9706 0.1419
>> mean(M)
ans =
0.6902 0.3888 0.7627 0.5962
>> mean(M')'
ans =
0.8404
0.6134
0.3408
0.6432
% 直接使用 mean( ) 函数是对每一列求平均数(下面的内容),
% 而有时候需要对每一列求平均数,则可以将 M 转置后求平均
% 再转置为一列,即对应于原来矩阵每一行的平均数。
一些特殊矩阵

-
linspace(x,y,n)
:线性间隔的向量。从x到y均等的给出n个数;
linspace(x,y)
:从x到y均等的给出100个数。 -
logspace(a,b)
:在 10
a
和10
b
之间生成50个对数间距点;
logspace(a,b,n)
:在10
a
和10
b
之间生成n个对数间距点;
注意不是均分
% logspace()不是均分
>> logspace(1,2,3)
ans =
10.0000 31.6228 100.0000
-
eye(n)
:n×n单位矩阵 -
diag()
:对角矩阵 -
rand()
:均匀分布的随机数(服从[0,1]上均匀分布)
一些矩阵相关的函数

-
max(A)
:给出每一列中最大的数 -
max(max(A))
:则可给出整个矩阵最大值
% max(A):给出每一列中最大的数
>> A=[8 1 6;3 5 7;4 9 2]
A =
8 1 6
3 5 7
4 9 2
>> max(A)
ans =
8 9 7
>> max(max(A))
ans =
9
-
左边一栏均类似给出每一列中xx,
mean()
:平均数
对于右边一栏
-
sort(A)
:对于每一列,从小到大排序。若只有一行,则对行从小到大排 -
sortrows(A)
:以行为单位(每行的数固定),按照第一列的数从小到大排
>> A=[8 1 6;3 5 7;4 9 2]
A =
8 1 6
3 5 7
4 9 2
>> sort(A) % 对每一列从小到大排序
ans =
3 1 2
4 5 6
8 9 7
>> sortrows(A) % 以行为单位,按照每行第一个数的大小对行排序
ans =
3 5 7
4 9 2
8 1 6
>> a=[4 6 2];
>> sort(a) % 若只有一行,则sort对行从小到大排
ans =
2 4 6
-
size(A)
:给出行宽和列宽 -
length(A)
:将A的各个维度的长度作比较,返回最大的那一个
>> A=rand(3,5)
A =
0.4218 0.9595 0.8491 0.7577 0.6555
0.9157 0.6557 0.9340 0.7431 0.1712
0.7922 0.0357 0.6787 0.3922 0.7060
>> size(A) %给出行宽和列宽
ans =
3 5
>> length(A) %给出行宽
ans =
5
-
find(A==x)
:给出矩阵A中等于x的元素位置(以列的形式呈现)
>> A=magic(3) % 给出一个3x3的magic矩阵
A =
8 1 6
3 5 7
4 9 2
>> A(3,2)=7; % 将(3,2)位置处的元素赋值为7
>> find(A==7) % 给出矩阵中等于7的元素位置
ans =
6
8
使用 strlength 而非 length 来确定字符串数组的每个元素中的字符数量。
length(str)结果为3
习题

%%
cos(sqrt((1+2+3+4)^3/5))
%sqrt( )是matlab内置的平方根函数
%%
sin(sqrt(pi))+log(tan(1))
%matlab中没有ln( )函数,log( )默认以e为底
%%
2^(3.5*1.7)
%%
exp(sin(10))
%matlab中要表示自然对数e,用exp(1)表示即可;表示以e为底数的指数函数用exp(n)(e的n次方)

format rat; %调整成分数显示
ans=3/13+4/14+5/15
format long; %调整成高精度小数显示
ans=3/13+4/14+5/15
以上内容为个人笔记,部分图片来源于郭老师课件或课程截图。
笔记汇总:
MATLAB基础教程
课程视频:
https://www.bilibili.com/video/BV1DA411Y7bN
课件下载:
MATLAB教程
郭彦甫老师的YouTube主页:
@Yanfu Kuo
原视频:
https://www.youtube.com/watch?v=KHFZLkm9qs0&t=8s

