维基百科:
贝塞尔曲线
以二次贝塞尔曲线的公式为例:
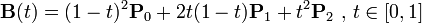
js函数:
//p0、p1、p2三个点,其中p0为起点,p2为终点,p1为控制点
//它们的坐标用数组表示[x,y]
//t的范围是0-1
function qBerzier(p0,p1,p2,t){
var x = (1 - t) * (1 - t) * p0[0] + 2 * t * (1 - t) * p1[0] + t * t * p2[0];
var y = (1 - t) * (1 - t) * p0[1] + 2 * t * (1 - t) * p1[1] + t * t * p2[1];
return [x,y];
}
通过函数,可以用L方法绘制贝塞尔曲线,但是这种方法是用直线将离散的点连接起来,只是因为点的距离很近,所以看上去是曲线,不够完美。所以绘制贝塞尔曲线,一般还是用path里的曲线命令比较好。
path路径绘制中,绘制贝塞尔曲线的命令包括:
Q 二次贝赛尔曲线 x1,y1 x,y
T 平滑二次贝塞尔曲线 x,y
C 曲线(curveto) x1,y1 x2,y2 x,y
S 平滑曲线 x2,y2 x,y
其中Q和T可以在一起使用,C和S可以在一起用。
Q 二次贝塞尔曲线
用法:M x0,y0 Q x1,y1 x2,y2
通过M定义(x0,y0)为起点,用Q定义(x1,y1)为控制点,(x2,y2)为终点,构成一条二次贝塞尔曲线。 Q方法非常简单直观。
T 二次贝塞尔曲线平滑延伸
用法:M x0,y0 Q x1,y1 x2,y2 T x4,y4
T 命令是二次被赛尔曲线的平滑延伸命令,用Q定义了一段二次贝塞尔曲线后面,紧接着一个T命令,只需定义终点,就可以自动延伸出一条平滑的曲线。 在这段曲线中,(x3,y3)没有手工定义,这里使用的T方法,只定义一个终点,起点是上一段曲线的终点,控制点则是上一段曲线的控制点的对称点(相对于 上一段曲线的终点)。 在这里,(x3,y3)是(x1,y1)的对称点(相对于(x2,y2)对称)。
C 三次贝塞尔曲线
用法:M x0,y0 C x1,y1 x2,y2 x3,y3
C方法定义的是三次贝塞尔曲线,这里只是多了一个控制点,很好理解
S 三次贝塞尔曲线平滑延伸
用法:M x0,y0 C x1,y1 x2,y2 x3,y3 S x5,y5 x6,y6
三次贝塞尔也有一个平滑延伸的命令,需要定义一个控制点和一个终点,命令会再自动生成一个控制点,从而形成一条延伸出来的三次贝赛尔曲线。



