基本流程
我们在这篇文章
没有公式,我们只谈决策树
里面跟大家简单的介绍了决策树是个啥东西。今天我们将深入的介绍一下决策树。
首先决策树是一类常见的机器学习方法,以二分类任务为例。我们希望从给定的数据集中学习一个模型用来对新的示例进行分类。
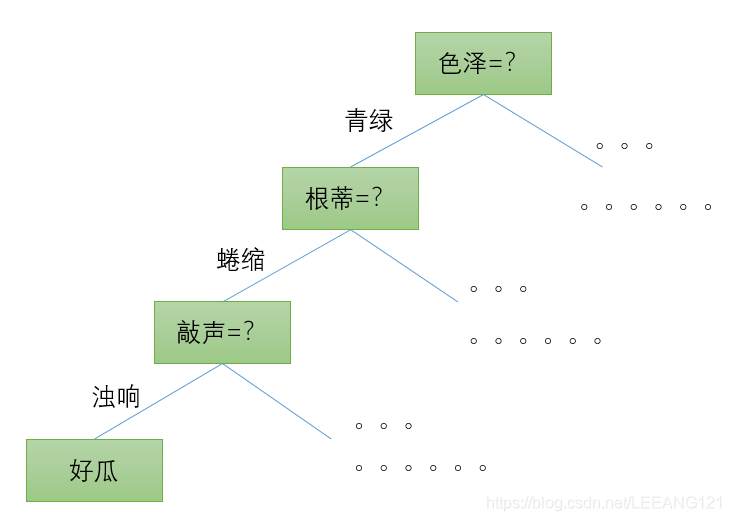
如下图所示:
这是一个我们选择西瓜时,判断该瓜是否为好瓜的决策过程。
那么什么是决策?
决策就是我们判断西瓜是不是好西瓜,这就是我们的决策,好西瓜我们就买,不是好西瓜就不买。
那么我们通过什么决策?
通过一系列西瓜特有的属性,例如这个西瓜的色泽如何?根蒂如何?敲击声音如何?等等等等。
决策树学习目的是为了产生一颗泛化能力强、可以处理未见示例的决策树。
显然,决策树是一个递归过程。在决策树算法中,有三种情况会导致递归返回:
1,当所有结点包含的样本属性全属于同一类别,无需划分;
2,当前属性集为空,或者所有样本在所有属性上取值相同,无法划分;
3,当前结点包含的样本集合为空,不能划分。
那么问题来了,上述三种情况具体是什么含义呢? 这里我用下面的西瓜选型图跟大家解释一下(个人理解)
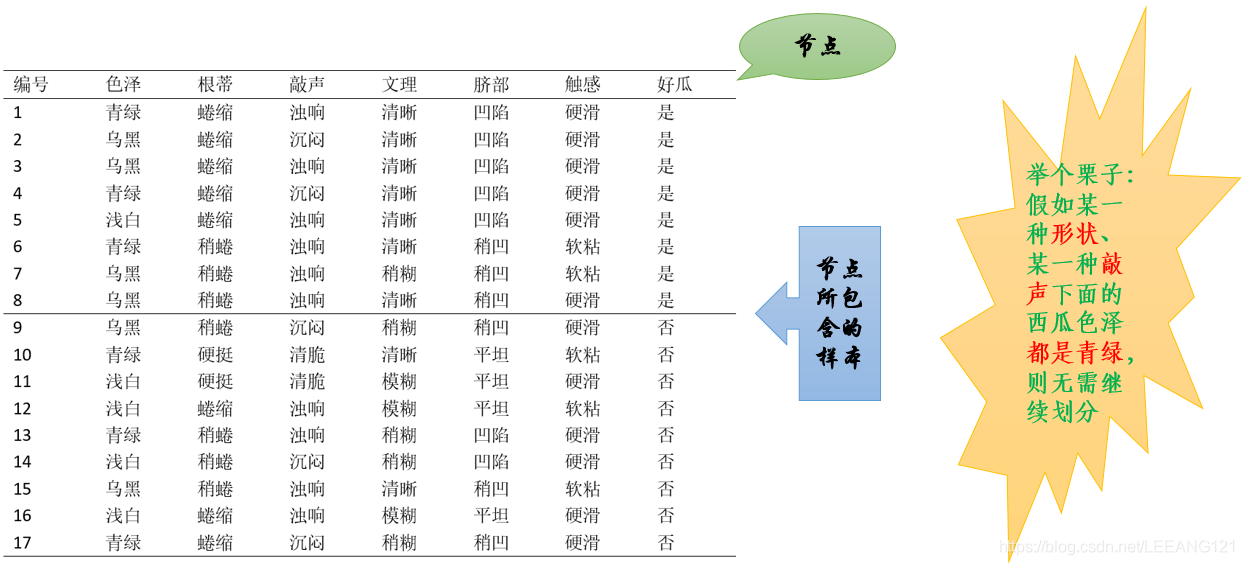
搞明白上面的基本概念之后,我们面临的下一个问题就是:
如何划分选择
从开篇第一幅图及上面的后续介绍,我们可以发现,决策过程其实就是不断划分的过程。我们是希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的’
纯度
‘会越来越高。
信息增益
大家看到这个名词的时候不用慌张,其实仔细想一想,仅从字面意思也不难理解,信息增益的意思就是指某条信息对整体的增幅情况。简单可以理解为该信息的
权重
。
在研究权重之前,我们先回到上面那个纯度的问题上,通常我们会用‘
信息熵
’来度量样本集合的纯度,熵这个词大家还有没有印象?如果忘记了可以参考我的一篇博文
啥也不会,照样看懂交叉熵损失函数
,这里有介绍熵的概念及公式。
当然这里我们也会简单进行一下说明:假定当前样本集合
D
D
D
中的第
k
k
k
类样本所占比例为
p
k
(
k
=
1
,
2
,
3
,
.
.
.
∣
y
∣
p_{k}(k=1,2,3,…|y|
p
k
(
k
=
1
,
2
,
3
,
.
.
.
∣
y
∣
,则
D
D
D
的信息熵为
E
n
t
(
D
)
=
−
∑
k
=
1
∣
y
∣
p
k
l
o
g
2
p
k
Ent(D)=-\sum_{k=1}^{\left | y \right |}p_{k}log_{2}p_{k}
E
n
t
(
D
)
=
−
∑
k
=
1
∣
y
∣
p
k
l
o
g
2
p
k
—————————————————————————————–公式1
E
n
t
(
D
)
Ent(D)
E
n
t
(
D
)
的值越小,则
D
D
D
的纯度越高。
我们假设离散属性
a
a
a
有
V
V
V
个可能的取值,我们用a对样本集
D
D
D
进行划分,会产生
V
V
V
个分支结点,其中第
v
v
v
个分支结点包含了
D
D
D
中所有在属性
a
a
a
上取值
a
v
a^{v}
a
v
的样本,记为
D
v
D^{v}
D
v
。我们可以根据上式计算出
D
v
D^{v}
D
v
的信息熵,考虑到不同的分支结点包含的样本数不同,我们给每个分支结点赋予权重
∣
D
v
∣
/
∣
D
∣
|D^{v}|/|D|
∣
D
v
∣
/
∣
D
∣
,最后我们可以计算出用属性
a
a
a
对样本
D
D
D
进行划分来获得
信息增量
。
(
标注:
针对上面这段话做一点简单的解释,首先什么是离散属性
a
a
a
,这本篇西瓜问题中,属性
a
a
a
指代表格中提到的色泽、根蒂、敲声、文理、脐部、触感这六个属性。取值为
a
v
a^{v}
a
v
的样本就好像取值为文理的样本,下面包含的内容越多,说明这个样本的权重越大。)信息增益的公式可以如下表示:
G
a
i
n
(
D
,
a
)
=
E
n
t
(
D
)
−
∑
v
=
1
V
D
v
D
E
n
t
(
D
v
)
Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{D^{v}}{D}Ent(D^{v})
G
a
i
n
(
D
,
a
)
=
E
n
t
(
D
)
−
∑
v
=
1
V
D
D
v
E
n
t
(
D
v
)
—————————————————————–公式2
通常信息增益越大,则意味着使用属性
a
a
a
划分获得的纯度提升越大,因此我们可以用信息增益来进行决策树的划分属性选择。
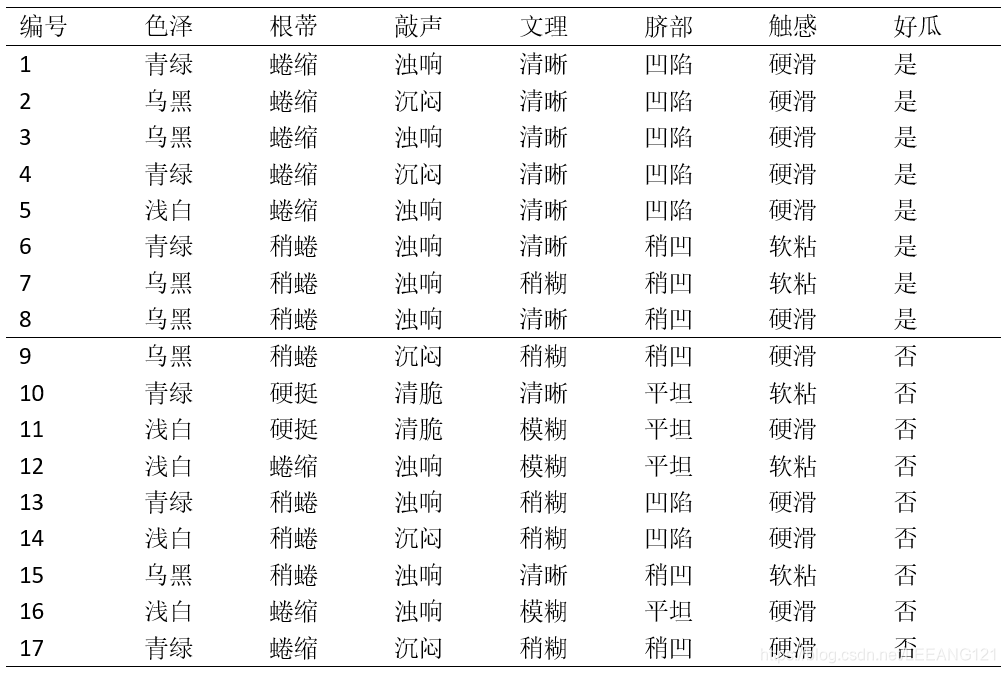
现在就以上面的西瓜数据表为例(为了方便阅读,我把数据单独再贴一份),这个数据集包含了17个训练样例,用来学习一颗未被刨开的西瓜是否是一个好瓜的决策树。这里显然
∣
y
∣
=
2
|y|=2
∣
y
∣
=
2
。在开始学习前,根节点包含了所有的样例
D
D
D
,其中正例
p
1
=
8
17
p_{1}=\frac{8}{17}
p
1
=
1
7
8
,反例
p
2
=
9
17
p_{2}=\frac{9}{17}
p
2
=
1
7
9
.根据公式1计算根节点的信息熵
E
n
t
(
D
)
=
−
∑
k
=
1
2
p
k
l
o
g
2
p
k
=
−
(
8
17
l
o
g
2
8
17
+
9
17
l
o
g
2
9
17
)
=
0.998
Ent(D)=-\sum_{k=1}^{2}p_{k}log_{2}p_{k}=-(\frac{8}{17}log_{2}\frac{8}{17}+\frac{9}{17}log_{2}\frac{9}{17})=0.998
E
n
t
(
D
)
=
−
∑
k
=
1
2
p
k
l
o
g
2
p
k
=
−
(
1
7
8
l
o
g
2
1
7
8
+
1
7
9
l
o
g
2
1
7
9
)
=
0
.
9
9
8
现在我们来计算每个属性的信息增益。
我们以属性’
色泽
‘为例,它有三个可能的取值(青绿、乌黑、浅白)。在我们利用这个色泽属性对D进行划分的时候,可以得到三个子集,我们把这三个子集分别记为:
D
1
D^{1}
D
1
(色泽=青绿)
D
2
D^{2}
D
2
(色泽=乌黑)
D
3
D^{3}
D
3
(色泽=浅白)
子集
D
1
D^{1}
D
1
包含编号为(1,4,6,10,13,17)的6个样例,在这六个样例中,正例占
3
6
\frac{3}{6}
6
3
,反例占
3
6
\frac{3}{6}
6
3
;
D
2
D^{2}
D
2
包含的编号为(2,3,7,8,9,15)的六个样例,其中正反例分别占
4
6
\frac{4}{6}
6
4
和
2
6
\frac{2}{6}
6
2
;
D
3
D^{3}
D
3
包含的编号为(5,11,12,14,16)五个例子,其中正反例分别占
1
5
\frac{1}{5}
5
1
和
4
5
\frac{4}{5}
5
4
.根据式1我们先分别求三个分支结点的信息熵:
E
n
t
(
D
1
)
=
−
(
3
6
l
o
g
2
3
6
+
3
6
l
o
g
2
3
6
)
=
1.000
Ent(D^{1})=-(\frac{3}{6}log_{2}\frac{3}{6}+\frac{3}{6}log_{2}\frac{3}{6})=1.000
E
n
t
(
D
1
)
=
−
(
6
3
l
o
g
2
6
3
+
6
3
l
o
g
2
6
3
)
=
1
.
0
0
0
E
n
t
(
D
2
)
=
−
(
4
6
l
o
g
2
4
6
+
2
6
l
o
g
2
2
6
)
=
0.918
Ent(D^{2})=-(\frac{4}{6}log_{2}\frac{4}{6}+\frac{2}{6}log_{2}\frac{2}{6})=0.918
E
n
t
(
D
2
)
=
−
(
6
4
l
o
g
2
6
4
+
6
2
l
o
g
2
6
2
)
=
0
.
9
1
8
E
n
t
(
D
3
)
=
−
(
1
5
l
o
g
2
1
5
+
4
5
l
o
g
2
4
5
)
=
0.722
Ent(D^{3})=-(\frac{1}{5}log_{2}\frac{1}{5}+\frac{4}{5}log_{2}\frac{4}{5})=0.722
E
n
t
(
D
3
)
=
−
(
5
1
l
o
g
2
5
1
+
5
4
l
o
g
2
5
4
)
=
0
.
7
2
2
现在我们把上述公式带入公式2
G
a
i
n
(
D
,
色
泽
)
Gain(D,色泽)
G
a
i
n
(
D
,
色
泽
)
=
E
n
t
(
D
)
−
∑
v
=
1
3
∣
D
v
∣
∣
D
∣
E
n
t
(
D
v
)
=Ent(D)-\sum_{v=1}^{3}\frac{\left |D^{v} \right |}{\left |D \right |}Ent(D^{v})
=
E
n
t
(
D
)
−
∑
v
=
1
3
∣
D
∣
∣
D
v
∣
E
n
t
(
D
v
)
=
0.998
−
(
6
17
×
1.000
+
6
17
×
0.918
+
5
17
×
0.722
)
=
0.109
=0.998-(\frac{6}{17}\times 1.000+\frac{6}{17}\times 0.918+\frac{5}{17}\times 0.722)=0.109
=
0
.
9
9
8
−
(
1
7
6
×
1
.
0
0
0
+
1
7
6
×
0
.
9
1
8
+
1
7
5
×
0
.
7
2
2
)
=
0
.
1
0
9
类似的,我们可以计算出其他属性的信息增益:
G
a
i
n
(
D
,
根
蒂
)
=
0.143
Gain(D,根蒂)=0.143
G
a
i
n
(
D
,
根
蒂
)
=
0
.
1
4
3
G
a
i
n
(
D
,
敲
声
)
=
0.141
Gain(D,敲声)=0.141
G
a
i
n
(
D
,
敲
声
)
=
0
.
1
4
1
G
a
i
n
(
D
,
纹
理
)
=
0.381
Gain(D,纹理)=0.381
G
a
i
n
(
D
,
纹
理
)
=
0
.
3
8
1
G
a
i
n
(
D
,
脐
部
)
=
0.289
Gain(D,脐部)=0.289
G
a
i
n
(
D
,
脐
部
)
=
0
.
2
8
9
G
a
i
n
(
D
,
触
感
)
=
0.006
Gain(D,触感)=0.006
G
a
i
n
(
D
,
触
感
)
=
0
.
0
0
6
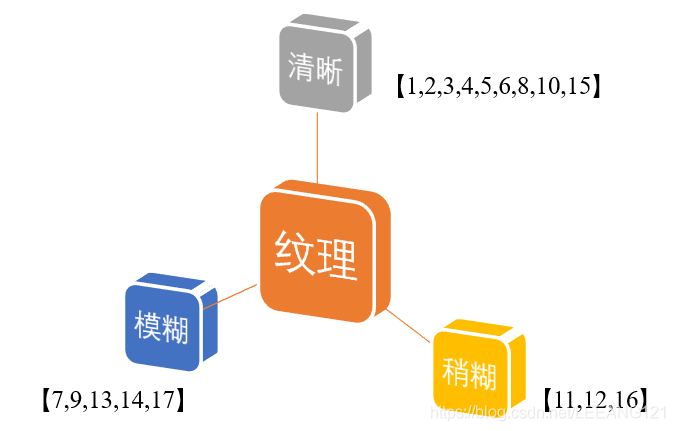
很明显,属性’纹理‘的信息增益最大,于是它被选择用来划分属性。
下图显示了基于‘纹理’对根节点进行划分的结果,各分支结点所包含的样例子集显示在结点中。
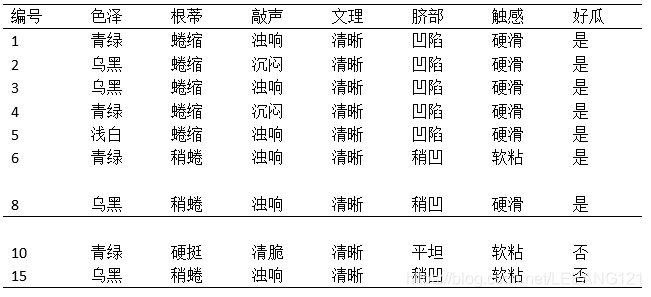
接下来,决策树算法将对每个分支结点做仅一步的划分。我们以上图分支结点(‘纹理=清晰’)为例,该结点包含的样例集合
D
1
D^{1}
D
1
中有编号为{1,2,3,4,5,6,8,10,15}的9个样例,这9个样例又分别包含了属性集合{色泽、根蒂、敲声、脐部、触感}。基于
D
1
D^{1}
D
1
计算出各属性的信息增益为:
G
a
i
n
(
D
1
,
色
泽
)
=
0.043
Gain(D^{1},色泽)=0.043
G
a
i
n
(
D
1
,
色
泽
)
=
0
.
0
4
3
G
a
i
n
(
D
1
,
根
蒂
)
=
0.458
Gain(D^{1},根蒂)=0.458
G
a
i
n
(
D
1
,
根
蒂
)
=
0
.
4
5
8
G
a
i
n
(
D
1
,
敲
声
)
=
0.331
Gain(D^{1},敲声)=0.331
G
a
i
n
(
D
1
,
敲
声
)
=
0
.
3
3
1
G
a
i
n
(
D
1
,
脐
部
)
=
0.458
Gain(D^{1},脐部)=0.458
G
a
i
n
(
D
1
,
脐
部
)
=
0
.
4
5
8
G
a
i
n
(
D
1
,
触
感
)
=
0.458
Gain(D^{1},触感)=0.458
G
a
i
n
(
D
1
,
触
感
)
=
0
.
4
5
8
tips
上面的计算过程还是要在简单说一下:
1,当我们以
D
1
D^{1}
D
1
中有编号为{1,2,3,4,5,6,8,10,15}的
9个样例
为集合时,我们可以假定西瓜数据集就剩下这9行(上述这9个数字所代表的属性行)
2,本来的
E
n
t
(
D
)
Ent(D)
E
n
t
(
D
)
中的分母由17变成了9,分子分别为7和2
3,此时计算得到的
E
n
t
(
D
)
=
0.764
Ent(D)=0.764
E
n
t
(
D
)
=
0
.
7
6
4
4,色泽=青绿的正概率为
3
/
4
3/4
3
/
4
、色泽=乌黑的正概率为
3
/
4
3/4
3
/
4
,色泽=浅白的正概率为
100
100%
1
0
0
5,以上为此时的计算说明。
‘根蒂’、‘脐部’、‘触感’3个属性均取得了最大的信息增益,可以任选其中之一作为划分属性。类似的,对每个分支结点进行上述操作,最终得到决策树如下:
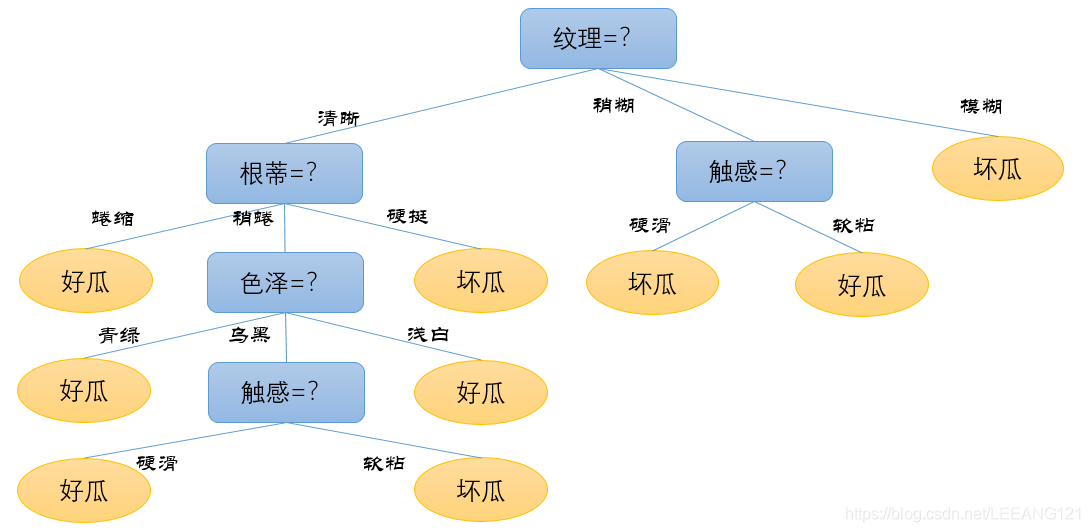
总结
以上就是决策树以及如何划分结点的详细说明,下一节我们会重点介绍:
增益率
基尼指数
剪枝处理
预剪枝
后剪枝
以上所有内容均来自周志华的《机器学习》,以及一点个人的心得。
这里还要感谢郭老师的大力支持。