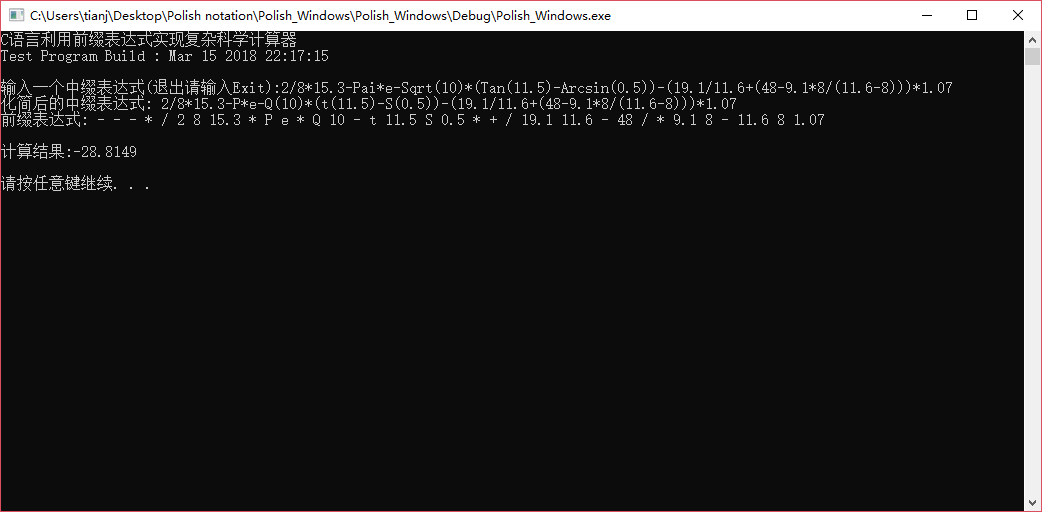
用C语言实现的科学计算器,支持2种常量,10种基本函数,Ans寄存器。相对来说拓展性应该是不错的,思路是首先化简复杂名称的函数名和常量名,然后把表达式转换成前缀表达式,再直接处理前缀表达式即可。因此对运算符和括号优先级的处理比较容易完美实现,执行效率也比较高,且无论输入表达式有多么复杂,只要确保输入缓冲区(定义在Analytic.h中)够大后面的都好说。
Analytic.c 运算库源文件,考虑到了移植方便的问题:
//Create Date: 2018-3-4
//Author: Charming
//File: Analytic.c
//Version: 1.7.2
//Last edit Date: 2018-3-13
//Directions: 表达式解析库源文件
// v1.0.0: 基本前缀表达式转换
// v1.1.0: 支持区分正负号与加减运算符的功能
// v1.2.0: 新增额外的多字节函数化简,并支持转换相应的前缀表达式
// v1.3.0: 新增支持符号常量参与表达式转换
// v1.3.5: 区分正负号与加减运算符功能的完善
// v1.4.0: 增加计算功能
// v1.5.0: 增加函数计算功能
// v1.6.0: 增加常数项功能
// v1.6.2: 增强表达式错误辨别能力
// v1.6.5: 提高常数精度
// v1.7.0: 新增三角函数的预期计算结果趋近于0或者不存在时的单独处理功能
// v1.7.2: 优化常数项遇到负号时的计算问题
// v1.7.7: 解决单目运算符计算顺序的Bug
#include "Analytic.h"
#include <string.h>
#include <math.h>
char *Expression = 0;//中缀表达式指针
a_size_t E_Ptr = 0;//中缀表达式操作位置标记
char *Polish_Notation = 0;//前缀表达式指针
a_size_t P_Ptr = 0;//前缀表达式操作位置标记
double Calc_ANS = 0;//答案寄存器
/*基本常数项(数值)Start*/
const_mode double _const_Euler_ = 2.718281828459045;//自然常数e
const_mode double _const_Pai_ = 3.141592653589793;//圆周率π
/*基本常数项(数值)End*/
/*基本常数项(符号)Start*/
const_mode char Ans[] = "Ans";//上一运算答案
#define S_Ans 'A'
const_mode char Pai[] = "Pai";//圆周率π的多字节符号
#define S_Pai 'P'
const_mode char Euler[] = "_e_";//自然常数,一般都使用e而不是_e_,
//复杂名的写法仅为避免名称重复陷入死循环,
//实际使用时直接用e即可
#define S_Euler 'e'
/*基本常数项(符号)End*/
/*基本函数项Start*/
const_mode char Ln[] = "ln";//自然对数
#define S_In 'I'
const_mode char Exp[] = "Exp";//自然指数
#define S_Exp 'E'
const_mode char Log[] = "log";//以10为底的对数
#define S_Log 'L'
const_mode char Sin[] = "Sin";//正弦函数
#define S_Sin 's'
const_mode char Cos[] = "Cos";//余弦函数
#define S_Cos 'c'
const_mode char Tan[] = "Tan";//正切函数
#define S_Tan 't'
const_mode char Sqrt[] = "Sqrt";//开方函数
#define S_Sqrt 'Q'
const_mode char ArcSin[] = "Arcsin";//反正弦函数
#define S_ArcSin 'S'
const_mode char ArcCos[] = "Arccos";//反余弦函数
#define S_ArcCos 'C'
const_mode char ArcTan[] = "Arctan";//反正切函数
#define S_ArcTan 'T'
/*基本函数项End*/
const_mode char *ComplexOperators[] = {//多字节函数名列表,顺序从长到短,有利于逻辑实别
ArcSin, ArcCos, ArcTan, Exp, Log, Sin, Cos, Tan, Sqrt, Ln
};
const_mode char SimpleOperators[] = {//单字节函数名列表,与多字节顺序需一一对应
S_ArcSin, S_ArcCos, S_ArcTan, S_Exp, S_Log, S_Sin, S_Cos, S_Tan,S_Sqrt, S_In
};
const_mode char *ComplexConstants[] = {//多字节常量名列表,顺序从长到短,有利于逻辑实别
Ans, Pai, Euler
};
const_mode char SimpleConstants[] = {//单字节常量名列表,与多字节顺序需一一对应
S_Ans, S_Pai, S_Euler
};
struct {
char data[SymbolMax];
w_size_t top;
}Symbol_Stack;//运算符栈
struct {
double data[NumberMax];
w_size_t top;
}Number_Stack;//运算符栈
typedef enum
{
Symbol, Number
}Stack_type;//栈类型
typedef enum
{
isNumber,
isNumberOrDot,
isBrackets,
isBracketLeft,
isBracketRight,
isOperatorsLevel3,
isOperatorsLevel2,
isOperatorsLevel1,
isOperatorsLevel0,
isConstants
}Symbol_type;//符号类型
void Init_Stack(Stack_type type)//堆栈初始化
{
switch (type)
{
case Symbol:
Symbol_Stack.top = -1;
break;
case Number:
Number_Stack.top = -1;
break;
default:
break;
}
}
Analytic_type Symbol_Push(void)//中缀表达式中的当前字符入栈
{
if (Symbol_Stack.top < SymbolMax - 1)
Symbol_Stack.data[++Symbol_Stack.top] = Expression[E_Ptr--];
else
return Conv_OverFlow;
return Conv_Ok;
}
Analytic_type Symbol_Pop(void)//从运算符栈出栈到前缀表达式
{
if (Symbol_Stack.top >= 0)
Polish_Notation[++P_Ptr] = Symbol_Stack.data[Symbol_Stack.top--];
else
return Conv_Exception;
return Conv_Ok;
}
w_size_t Get_StringLen(char *str, const w_size_t Maxlen)//计算表达式长度
{
#if USESTRINGLIB == 0
w_size_t len = 0;
while (str[len] != '\0' && len < Maxlen)
{
len++;
}
return len;
#else
return (w_size_t)strnlen(str, Maxlen);
#endif
}
#if STRINGLIB_standard == 1
char* my_strrev(char* s)
{
char* h = s;
char* t = s;
char ch;
while (*t++) {};
t -= 2;//与t++抵消、回跳过结束符'\0'
while (h < t)//当h和t未重合时,交换它们所指向的字符
{
ch = *h;
*h++ = *t; /* h向尾部移动 */
*t-- = ch; /* t向头部移动 */
}
return s;
}
#endif
void Make_String_Reverse(char *str, const w_size_t Maxlen)//字符串反转
{
w_size_t len;
len = Get_StringLen(str, Maxlen);
if (str[len - 1] == ' ')
{
str[len - 1] = 0;
}
#if STRINGLIB_standard == 1
my_strrev(str);
#else
strrev(str);
#endif
}
unsigned char Check(char *chr, Symbol_type type)//判断字符或字符串的类型
{
a_size_t i;
switch (type)
{
case isNumber:
if (*chr >= '0' && *chr <= '9')
return 1;
break;
case isNumberOrDot:
if (*chr >= '0' && *chr <= '9' || *chr == '.')
return 1;
break;
case isBrackets:
if (*chr == '(' || *chr == ')')
return 1;
break;
case isBracketLeft:
if (*chr == '(')
return 1;
break;
case isBracketRight:
if (*chr == ')')
return 1;
break;
case isOperatorsLevel0:
for (i = 0; i < sizeof(SimpleOperators); i++)
if (*chr == SimpleOperators[i])
return 1;
break;
case isOperatorsLevel1:
if (*chr == '^')
return 1;
break;
case isOperatorsLevel2:
if (*chr == '*' || *chr == '/')
return 1;
break;
case isOperatorsLevel3:
if (*chr == '+' || *chr == '-')
return 1;
break;
case isConstants:
for (i = 0; i < sizeof(SimpleConstants); i++)
if (*chr == SimpleConstants[i])
return 1;
break;
default:
break;
}
return 0;
}
Analytic_type Convert_to_Polish(void)//中缀表达式到前缀表达式的转换程序
{
Analytic_type AnserReg;
unsigned char tempflag;
P_Ptr = -1;
Init_Stack(Symbol);
E_Ptr = (a_size_t)Get_StringLen(Expression, Exprlen);
while (E_Ptr >= 0)//逆序处理
{
if (Check(&Expression[E_Ptr], isNumber))//处理数值情况
{
tempflag = 0;//这里tempflag用于处理一个特殊情况(见下面代码),
//使用goto容易造成复杂的意外情况,因此改用单独设立的标志位和死循环配合实现
while (1)
{
while (tempflag == 1 || (E_Ptr >= 0) && Check(&Expression[E_Ptr], isNumberOrDot))
{
tempflag = 0;
Polish_Notation[++P_Ptr] = Expression[E_Ptr--];//将数值或小数点转入前缀表达式
}
if ((E_Ptr >= 0) && //中缀表达式中还有没处理的
((E_Ptr == 0 && Check(&Expression[E_Ptr], isOperatorsLevel3)) ||
Check(&Expression[E_Ptr], isOperatorsLevel3) &&
!(Check(&Expression[E_Ptr - 1], isNumber) || Check(&Expression[E_Ptr - 1], isConstants)) &&
!Check(&Expression[E_Ptr - 1], isBracketRight)))
//由于三级运算符('+' '-')可做正负号使用,因此对单独存在的三级运算符当做数的一部分处理,
//即如果当前字符是最后一个字符,且是三级运算符,或者这并不是最后一个字符,且下一个字符
//不是右括号、不是数字或常量的情况下,这个三级运算符需要当作数处理。
tempflag = 1;
else
break;
}
Polish_Notation[++P_Ptr] = ' ';//前缀表达式添加空格分隔符
}
else if (Check(&Expression[E_Ptr], isConstants))//待处理的是常量
{
Polish_Notation[++P_Ptr] = Expression[E_Ptr--];//将常量符号转入前缀表达式
if ((E_Ptr >= 0) && //中缀表达式中还有没处理的
((E_Ptr == 0 && Check(&Expression[E_Ptr], isOperatorsLevel3)) ||
Check(&Expression[E_Ptr], isOperatorsLevel3) &&
!(Check(&Expression[E_Ptr - 1], isNumber) || Check(&Expression[E_Ptr - 1], isConstants)) &&
!Check(&Expression[E_Ptr - 1], isBracketRight)))
//对符号单独处理,原理类似于常数的处理方法
Polish_Notation[++P_Ptr] = Expression[E_Ptr--];//将常量符号转入前缀表达式
Polish_Notation[++P_Ptr] = ' ';//前缀表达式添加空格分隔符
}
else if (Check(&Expression[E_Ptr], isBracketRight))//待处理的字符是右括号
{
if ((AnserReg = Symbol_Push()) != Conv_Ok)//压入运算符栈,如果异常,则返回异常情况,压栈过程同时E_Ptr也移动,不需要重复操作
return AnserReg;
}
else if (Check(&Expression[E_Ptr], isBracketLeft))//待处理的字符是左括号
{
while (!Check(&Symbol_Stack.data[Symbol_Stack.top], isBracketRight))//如果运算符栈栈顶不是右括号
{
if ((AnserReg = Symbol_Pop()) != Conv_Ok)//运算符出栈
return AnserReg;
Polish_Notation[++P_Ptr] = ' ';//出一次加一个空格
}
Symbol_Stack.data[Symbol_Stack.top--] = '\0';//封栈,删除栈顶外内容
E_Ptr--;//处理下一位
}
else if (Check(&Expression[E_Ptr], isOperatorsLevel3))//待处理字符是'+'或'-'
{
while (Symbol_Stack.top >= 0 &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel3) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isBracketRight))
//运算符栈非空,且栈顶不是')' '+' '-'的时候要先出栈,实际上这里是比较优先级,'*' '/' '^'的优先级更高,所以要先出栈
{
if ((AnserReg = Symbol_Pop()) != Conv_Ok)//运算符出栈到前缀表达式
return AnserReg;
Polish_Notation[++P_Ptr] = ' ';//出一次加一个空格
}
if ((AnserReg = Symbol_Push()) != Conv_Ok)//压栈
return AnserReg;
}
else if (Check(&Expression[E_Ptr], isOperatorsLevel2))//待处理字符是'*'或'/'
{
while (Symbol_Stack.top >= 0 &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel3) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel2) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isBracketRight))
//运算符栈非空,且栈顶不是')' '+' '-' '*' '/'的时候要先出栈,原理同上
{
if ((AnserReg = Symbol_Pop()) != Conv_Ok)//运算符出栈到前缀表达式
return AnserReg;
Polish_Notation[++P_Ptr] = ' ';//出一次加一个空格
}
if ((AnserReg = Symbol_Push()) != Conv_Ok)//压栈
return AnserReg;
}
else if (Check(&Expression[E_Ptr], isOperatorsLevel1))//待处理字符是'^',原理同上
{
while (Symbol_Stack.top >= 0 &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel3) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel2) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel1) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isBracketRight))
//运算符栈非空,且栈顶不是')' '+' '-' '*' '/' '^'的时候要先出栈,原理同上
{
if ((AnserReg = Symbol_Pop()) != Conv_Ok)//运算符出栈到前缀表达式
return AnserReg;
Polish_Notation[++P_Ptr] = ' ';//出一次加一个空格
}
if ((AnserReg = Symbol_Push()) != Conv_Ok)//压栈
return AnserReg;
}
else if (Check(&Expression[E_Ptr], isOperatorsLevel0))//若待处理的是一元运算符
{
if (E_Ptr > 0 && //单目运算符前有值或括弧
Check(&Expression[E_Ptr - 1], isNumberOrDot) ||
Check(&Expression[E_Ptr - 1], isBracketRight) ||
Check(&Expression[E_Ptr - 1], isConstants))
return Conv_MathError;
while (Symbol_Stack.top >= 0 &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel3) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel2) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel1) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isOperatorsLevel0) &&
!Check(&Symbol_Stack.data[Symbol_Stack.top], isBracketRight))
//原理同上
{
if ((AnserReg = Symbol_Pop()) != Conv_Ok)//运算符出栈到前缀表达式
return AnserReg;
Polish_Notation[++P_Ptr] = ' ';//出一次加一个空格
}
if ((AnserReg = Symbol_Push()) != Conv_Ok)//压栈
return AnserReg;
}
else//其他的东西就直接都忽略掉吧
{
E_Ptr--;
}
}
while (Symbol_Stack.top >= 0)//操作符栈没有变空,说明有操作符没有取出来
{
if ((AnserReg = Symbol_Pop()) != Conv_Ok)//运算符出栈到前缀表达式
return AnserReg;
Polish_Notation[++P_Ptr] = ' ';//出一次加一个空格
}
Polish_Notation[++P_Ptr] = Symbol_Stack.data[++Symbol_Stack.top] = '\0';//最后结尾加一个截至符
Make_String_Reverse(Polish_Notation, Polishlen);
return Conv_Ok;
}
Init_type Analytic_Init(Init_type type, char *address)//表达式初始化
{
switch (type)
{
case Init_Expression://初始化中缀表达式
Expression = address;
break;
case Init_Polish_Notation://初始化前缀表达式
Polish_Notation = address;
break;
default:
return Init_Error;
}
return Init_Ok;
}
void ReplaceStringtoChar(char *str, const char *tar, const char chr)//替换表达式中的复杂函数名
{
w_size_t position;
char *tarposition;
w_size_t tarsize;
tarsize = (w_size_t)strlen(tar);
while ((tarposition = strstr(str, tar)) != NULL)
{
position = tarposition - str;
str[position++] = chr;
while (str[position + tarsize - 1] != 0)
{
str[position] = str[position + tarsize - 1];
position++;
}
str[position] = 0;
}
}
char *Analytic_Simplification(char *str)//复杂函数名化简功能
{
a_size_t i;
for (i = 0; i < sizeof(SimpleOperators); i++)//替换操作符
ReplaceStringtoChar(str, ComplexOperators[i], SimpleOperators[i]);
for (i = 0; i < sizeof(SimpleConstants); i++)//替换常量名
ReplaceStringtoChar(str, ComplexConstants[i], SimpleConstants[i]);
return str;
}
double Store(char *str, w_size_t *p)//转换字符到浮点数
{
w_size_t j = *p - 1, i;
double n = 0, m = 0;
switch (str[*p])
{
case S_Ans:
if (str[*p - 1] == '-')
{
*p = *p - 1;
return (-1 * Calc_ANS);
}
else
return Calc_ANS;
case S_Pai:
if (str[*p - 1] == '-')
{
*p = *p - 1;
return (-1 * _const_Pai_);
}
else
return _const_Pai_;
case S_Euler:
if (str[*p - 1] == '-')
{
*p = *p - 1;
return (-1 * _const_Euler_);
}
else
return _const_Euler_;
default:
break;
}
while (str[j] >= '0' && str[j] <= '9')
j--;
if (str[j] != '.')
for (i = j + 1; i <= *p; i++)
n = 10 * n + (str[i] - '0');
else
{
for (i = j + 1; i <= *p; i++)
m = m + pow(0.1, i - j) * (str[i] - '0');
if (str[j] == '.')
{
*p = --j;
while (str[j] >= '0' && str[j] <= '9')
j--;
for (i = j + 1; i <= *p; i++)
n = 10 * n + (str[i] - '0');
}
}
*p = j;
if (str[*p] == '-') return(-(n + m));
return(n + m);
}
Analytic_type Number_Push(w_size_t *i)//数值入栈
{
if (Number_Stack.top < NumberMax - 1)
Number_Stack.data[++Number_Stack.top] = Store(Polish_Notation, i);
else
return Conv_OverFlow;
return Conv_Ok;
}
double Clear_Infinitesimal(double ans)
{
if (ans < 1e-10 && ans > -1e-10)
return 0;
else
return ans;
}
double Clear_ComplexTan(double num)
{
double r1, r2;
int i = (int)(num / (_const_Pai_ / 2));
r1 = num - i * (_const_Pai_ / 2) + 1e-15;
r2 = (i + 1) * (_const_Pai_ / 2) - num + 1e-15;
if (i % 2 != 0 &&
((r1 > 0 && r1 < 1e-10) ||
(r2 > 0 && r2 < 1e-10)))
return NAN;
return num;
}
Analytic_type Number_Pop(w_size_t i)//数值出栈
{
if (Number_Stack.top >= 0)
{
if (Polish_Notation[i] != ' ')
switch (Polish_Notation[i])
{
case '+':
Number_Stack.data[Number_Stack.top - 1] =
Number_Stack.data[Number_Stack.top] + Number_Stack.data[Number_Stack.top - 1];
Number_Stack.top--;
break;
case '-':
Number_Stack.data[Number_Stack.top - 1] =
Number_Stack.data[Number_Stack.top] - Number_Stack.data[Number_Stack.top - 1];
Number_Stack.top--;
break;
case '*':
Number_Stack.data[Number_Stack.top - 1] =
Number_Stack.data[Number_Stack.top] * Number_Stack.data[Number_Stack.top - 1];
Number_Stack.top--;
break;
case '/':
Number_Stack.data[Number_Stack.top - 1] =
Number_Stack.data[Number_Stack.top] / Number_Stack.data[Number_Stack.top - 1];
Number_Stack.top--;
break;
case '^':
Number_Stack.data[Number_Stack.top - 1] =
pow(Number_Stack.data[Number_Stack.top], Number_Stack.data[Number_Stack.top - 1]);
Number_Stack.top--;
break;
case S_In:
Number_Stack.data[Number_Stack.top] = log(Number_Stack.data[Number_Stack.top]);
break;
case S_Log:
Number_Stack.data[Number_Stack.top] = log10(Number_Stack.data[Number_Stack.top]);
break;
case S_Exp:
Number_Stack.data[Number_Stack.top] = pow(_const_Euler_, Number_Stack.data[Number_Stack.top]);
break;
case S_Sin:
Number_Stack.data[Number_Stack.top] = sin(Number_Stack.data[Number_Stack.top]);
Number_Stack.data[Number_Stack.top] = Clear_Infinitesimal(Number_Stack.data[Number_Stack.top]);
break;
case S_Cos:
Number_Stack.data[Number_Stack.top] = cos(Number_Stack.data[Number_Stack.top]);
Number_Stack.data[Number_Stack.top] = Clear_Infinitesimal(Number_Stack.data[Number_Stack.top]);
break;
case S_Tan:
Number_Stack.data[Number_Stack.top] = Clear_ComplexTan(Number_Stack.data[Number_Stack.top]);
Number_Stack.data[Number_Stack.top] = tan(Number_Stack.data[Number_Stack.top]);
Number_Stack.data[Number_Stack.top] = Clear_Infinitesimal(Number_Stack.data[Number_Stack.top]);
break;
case S_Sqrt:
Number_Stack.data[Number_Stack.top] = sqrt(Number_Stack.data[Number_Stack.top]);
break;
case S_ArcSin:
Number_Stack.data[Number_Stack.top] = asin(Number_Stack.data[Number_Stack.top]);
break;
case S_ArcCos:
Number_Stack.data[Number_Stack.top] = acos(Number_Stack.data[Number_Stack.top]);
break;
case S_ArcTan:
Number_Stack.data[Number_Stack.top] = atan(Number_Stack.data[Number_Stack.top]);
break;
}
}
else
return Conv_MathError;
return Conv_Ok;
}
Analytic_type Calculation_Results(void)
{
Analytic_type res;
w_size_t len, i;
Init_Stack(Number);
len = Get_StringLen(Polish_Notation, Polishlen);
for (i = len - 1; i >= 0; i--)
{
if (Check(&Polish_Notation[i], isNumber) || Check(&Polish_Notation[i], isConstants) ||
(Check(&Polish_Notation[i], isOperatorsLevel3) && Check(&Polish_Notation[i + 1], isNumber)))
{
if ((res = Number_Push(&i)) != Conv_Ok)
return res;
}
else
{
if ((res = Number_Pop(i)) != Conv_Ok)
return res;
}
}
if (Symbol_Stack.top != 0 || Number_Stack.top != 0)
return Conv_MathError;
return Conv_Ok;
}
Analytic_type Analytic(Analytic_type type)//表达式解析
{
switch (type)
{
case Conv_to_Polish:
return Convert_to_Polish();
case Calc_Results:
return Calculation_Results();
default:
break;
}
return Conv_Exception;
}
double Get_Answer(void)
{
return (Calc_ANS = Number_Stack.data[0]);
}
Analytic.h 头文件,另外还包括几个重要的枚举类型:
//Create Date: 2018-3-4
//Author: Charming
//File: Analytic.h
//Directions: 表达式解析库头文件
//Last edit Date: 2018-3-6
#ifndef __ANALYTIC_H_
#define __ANALYTIC_H_
#define const_mode const
#define USESTRINGLIB 1
#define STRINGLIB_standard 1
#ifndef NULL
#define NULL 0
#endif
#define Exprlen 100
#define Polishlen 180
#define SymbolMax 80
#define NumberMax 50
typedef signed char a_size_t;
typedef signed short w_size_t;
typedef enum//初始化枚举类型
{
Init_Expression,
Init_Polish_Notation,
Init_Ok,
Init_Error
}Init_type;
typedef enum
{
Conv_to_Polish,
Calc_Results,
Conv_Ok,
Conv_MathError,
Conv_OverFlow,
Conv_Exception
}Analytic_type;
Init_type Analytic_Init(Init_type type, char *address);
Analytic_type Analytic(Analytic_type type);
char *Analytic_Simplification(char *str);
double Get_Answer();
#endif
另外我贴上我测试用的 main.c,也可以作为使用方法的参考:
//Create Date: 2018-3-4
//Author: Charming
//File: Analytic.c
//Version: 1.7.2
//Last edit Date: 2018-3-15
//Directions: 测试源文件
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "Analytic.h"
char E_String[Exprlen] = { 0 };
char P_String[Polishlen] = { 0 };
int main(void)
{
Analytic_type res;
Analytic_Init(Init_Expression, E_String);
Analytic_Init(Init_Polish_Notation, P_String);
while (1)
{
system("cls");
printf("C语言利用前缀表达式实现复杂科学计算器\r\n");
printf("Test Program Build : %s %s\r\n\r\n", __DATE__, __TIME__);
printf("输入一个中缀表达式(退出请输入Exit):");
gets_s(E_String, sizeof(E_String));
if (strnicmp(E_String, "exit", 4) == 0)
return 0;
printf("化简后的中缀表达式: %s\r\n", Analytic_Simplification(E_String));
if ((res = Analytic(Conv_to_Polish)) == Conv_Ok)
res = Analytic(Calc_Results);
switch (res)
{
case Conv_Ok:
printf("前缀表达式: %s\r\n", P_String);
printf("\r\n计算结果:%g\r\n\r\n", Get_Answer());
break;
case Conv_MathError:
printf("\r\n数学错误!\r\n\r\n");
break;
case Conv_OverFlow:
printf("\r\n堆栈溢出!\r\n\r\n");
break;
case Conv_Exception:
printf("\r\n系统异常!\r\n\r\n");
break;
default:
break;
}
system("pause");
}
return 0;
}
测试截图:
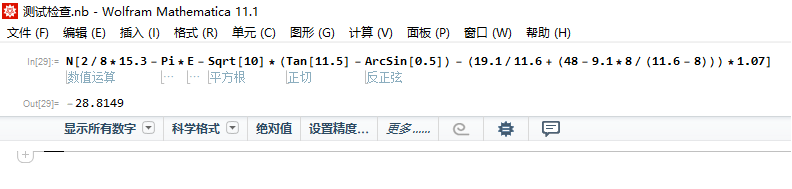
Mathematica验证:
版权声明:本文为MobiuX原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。