前言
我们所知的八大内部的排序算法有冒泡排序、选择排序、快速排序、归并排序、链式基数排序、插入排序、希尔排序、堆排序、而这篇文章主要研究这其中的希尔排序和堆排序算法,之前的排序算法都在下面连接中介绍过,因此不在过多的赘述
五大经典算法-分治法 及其应用二分查找 、快速排序、递归排序
插入排序
插入排序顾名思义直接插入,打掉一个放一个在放数据时,直接进行排序,这样一描述是不是对于小数据量的数据排序效率还是很高的
- 首先拿出一个进行比较排序
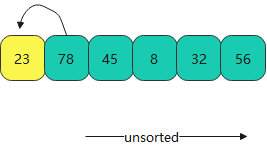
- 进行比较出来得到前两个顺序的值
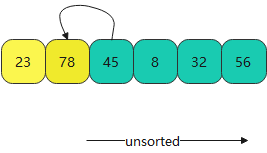
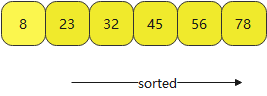
- 到第三轮时,45插入的点就在23前面
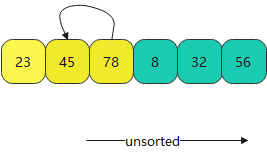
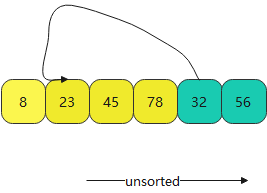
- 最后不断得到下面排序好的数据,这就是插入排序算法
这并不是一种数据交换的思维,而是直接插入移动数据的思想
代码实现
-
首先创建一个无序的数组
int[] array=new int[]{2,3,4,5,6,7,1,8,9};- 从1开始只要 当前的点小于0,则赋值给当前值,然后 是不断插入的
int j=1;
int target=array[j];
while(j>0 && target<array[j-1]){
array[j]=array[j-1];//
j--;//这个地方是不断往遍历的,如果是1 则跳出去
}
array[j]=target;//如果1上的数据比0上的数据小,那这里的j已经变成了 0了,才插入- 然后遍历所有的就是整个插入排序了
for (int i = 1; i < array.length; i++) {
int j=i;
int target=array[j];
while(j>0 && target<array[j-1]){
array[j]=array[j-1];
j--;
}
array[j]=target;
}
这就是整个插入排序,是比较简单的,总的来说,只要比当前值小,就往后移动,然后直到移动完了,在放到插入的地方。这和冒泡排序算法和快速排序是两种思想,不要弄混了
希尔排序
运用在一些大量重复排序,自身有很多都是有序,然后采用该算法的话,效率是相当的高
的
核心思想
取一个定长的值比如6,也就是固定长度数据之间进行使用插入排序进行排序好,直到全部固定长度数据进行排序,经过一轮;大部分数据就排序好了;然后继续定值去调整, 如果其中完成插入一次的操作,我们就可以完成了,就相当于排序成功了;如果固定长度取得好,可以减少非常多排序动作。
已知的最好步长序列由Marcin Ciura设计(1,4,10,23,57,132,301,701,1750,…)
这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。” 用这样步长序列的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快, 但是在涉及大量数据时希尔排序还是比快速排序慢。

很多数据已经排序好了数据,其他算法都会有很多不必要得逻辑运算。
代码实现
主要是在插入排序上进行改进,首先将插入排序进行复制过来
for (int i = 1; i < array.length; i++) {
int j=i;
int target=array[j];
while(j>0 && target<array[j-1]){
array[j]=array[j-1];
j--;
}
array[j]=target;
}-
然后进行改造,首先固定长度为3进行排序。
//直接插入排序 step 为固定长度进行排序
for (int i = 0 + step; i < array.length; i = i + step) {
int j = i;
int target = array[j];
while (j > step - 1 && target < array[j - step]) {
array[j] = array[j - step];
j = j - step;
}
array[j] = target;
}-
而在整合起来完整得希尔排序
public static void shellSort(int[] array,int step){
for(int k=0;k<step;k++) {
//直接插入排序
for (int i = k + step; i < array.length; i = i + step) {
int j = i;
int target = array[j];
while (j > step - 1 && target < array[j - step]) {
array[j] = array[j - step];
j = j - step;
}
array[j] = target;
}
}
}
希尔排序适合小数组进行排序,需要进行多次排序
shellSort(array,4);
//2 3 1 5 6 7 4 8 9
shellSort(array,1);- 时间复杂度是非常难确定得,根据定长值来确定的
堆排序
堆的概念
近似于完全二叉树的概念,也就是
leftNo = [2
n+1]
rightNo = [2
(n+1)];
堆排序是什么
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。这就是最大顶堆,而我们在PriorityQueue 优先队列中采用最小顶堆排序

大家可以看看我分析的jdk中集合源码分析
Java 集合深入理解 (九) :优先队列(PriorityQueue)之源码解读,及最小顶堆实现研究
我们继续分析堆排序的过程 大顶堆
- 从最后一个非叶子节点开始,每三个节点做一次大小比较,最小的做根如果移动过程中如果子树上的顺序被破坏了,子树上重新调整三个节点的位置
- 取走整个树的根节点,把最后一个叶子做为根节点
- 重复1和2,直到所有节点被取走了



这里怎么找到父节点和做节点和右节点
父节点是: (n-1)/2
左孩子是: 2*n+1
右孩子是: 2*n+2
代码实现
-
首先创建一个调整堆的方法,并记录起始的位置
/**
* 调整堆
*/
void maxHeapify(int array[],int start,int end){
//父亲的位置
int dad=start;
//儿子的位置
int son=dad*2+1;
}-
当我们从中间进行调整时,包括子节点都有可能需要调整,如果子节点下标在可以调整的范围内就一直调整下去。
/**
* 调整堆
*/
void maxHeapify(int array[],int start,int end){
//父亲的位置
int dad=start;
//儿子的位置
int son=dad*2+1;
while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
}
}-
如果没有右孩子就不用比,有的话,比较两个儿子,选择最大的出来
/**
* 调整堆
*/
void maxHeapify(int array[],int start,int end){
//父亲的位置
int dad=start;
//儿子的位置
int son=dad*2+1;
while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
//如果没有右孩子就不用比,有的话,比较两个儿子,选择最大的出来
if(son+1 <= end && array[son]<array[son+1]){
son++;
}
}
}-
这里需要对进行调整
/**
* 调整堆
*/
void maxHeapify(int array[],int start,int end){
//父亲的位置
int dad=start;
//儿子的位置
int son=dad*2+1;
while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
//如果没有右孩子就不用比,有的话,比较两个儿子,选择最大的出来
if(son+1 <= end && array[son]<array[son+1]){
son++;
}
//和父节点比大小
if(array[dad]>array[son]){
return;
}else{//父亲比儿子小,就要对整个子树进行调整
int temp=array[son];
array[son]=array[dad];
array[dad]=temp;
//递归下一层
dad=son;
son=dad*2+1;
}
}
}-
开始进行建堆
void heapSort(int array[],int len){
//建堆 len/2-1最后一个非叶子节点
for(int i=len/2-1;i>=0;i--){
maxHeapify(array,i,len-1);
}
}-
排序,根节点和最后一个节点交换,换完以后,取走根,重新建堆,len-1 最后一个节点
void heapSort(int array[],int len){
for(int i=len-1;i>0;i--){
int temp=array[0];
array[0]=array[i];
array[i]=temp;
maxHeapify(array,0,i-1);
}
}-
最后完整的代码
void heapSort(int array[],int len){
for(int i=len/2-1;i>=0;i--){
maxHeapify(array,i,len-1);
}
for(int i=len-1;i>0;i--){
int temp=array[0];
array[0]=array[i];
array[i]=temp;
maxHeapify(array,0,i-1);
}
}
应用场景
在大数据情况下找到前n个数据
八大内部排序的各大应用场景
-
冒泡排序:针对8个以内的数据,速度是很快的
-
选择排序:针对8个以内的数据,速度也是很快的
-
快速排序:针对的是数据量大,并且是线性结构,但大量重复数据和链式结构不适合采用二分的思想
-
归并排序:针对大量排序方式,重复数据,链式结构,但是空间要求相当大
-
链式基数:有多关键字排序,可以考虑这种方式
-
插入排序:也是针对小数据量
-
希尔排序:针对比较多的重复数据
-
堆排序:应用在大数据下找前n个数据
平常我们在算法的选择,根据业务场景和算法的特点来选择的。
总结
整篇文章我主要分析了各种不同排序方式的应用场景。然后 像希尔排序的核心还是在插入排序,然后冒泡和选择排序是一类的,而快排的基础是选择排序,归并和快排的核心思想来源于二分;堆排序则是来源与堆的特性 。各种排序都是有联系的。而在不同的业务场景选择不同的方法是主要思想。