一、矩阵的介绍
1.1矩阵特征
矩阵也称为二维数组,从表面上不符合线性表的特征,表现在一下三个方面:
(1).首结点不唯一,每一行和每一列都有一个首结点;
(2).尾结点也不唯一,每一行和每一列都有一个尾结点;
(3).中间结点有两个直接前驱和两个直接后驱,即在行和列的方向上各有一个直接前驱,也各有一个直接后驱;
但是,实质上,我们可以把每行(或者每列)数据看成一个整体,作为一个数据元素,那么矩阵就由一列(或一行)数据元素组成。 从这个角度看,矩阵完全符合线性表的特征,只是每个数据元素的类型又是一个线性表。 因此,矩阵可以看成是线性表的一种推广 ,多维数组、广义表又是线性表另一种更复杂的推广。
1.2 矩阵存储方式
(1).按行优先顺序存储,即将数组元素按行排序,第i+1行的第一个元素紧接在第i行的最后1个元素的后面。
(2).按列有限顺序存储,即将数组元素按列排序,第j+1列的第一个元素紧接在第j列的最后1个元素的后面。
注意:按照上述两种方式
顺序存储的 m x n 矩阵A
,只要知道第一个元素的存储地址
a11(即基地址)
、维数以及
每个元素所占用的字节数c
:
按行优先顺序存储时,aij的存储地址为:aij = a11 + ((i-1) x n +(j-1)) x c
按列优先顺序存储时,aij的存储地址为:aij = a11 + ((j-1) x m +(i-1)) x c
二、特殊矩阵
大小为nXn的矩阵采用顺序结构存储时,所需要的存储空间总是固定的,即nXnXc(c为每个数据元素所需存储空间)。然而,在实际应用中,矩阵中往往有许多相同的元素(或零元素),如果仍然采用4.2. 1节中的存储方法进行存储,将大大浪费存储空间。因此,为了节省存储空间,可以对这类矩阵进行压缩存储。所谓压缩存储,就是为相同的元素只分配一个存储空间(零元素不分配空间)。这种数据值相同的元素或者零元素的分布有一定规律的矩阵称为特殊矩阵,主要分为三类:对称矩阵、三角矩阵和稀疏矩阵。
2.1对称矩阵
在一个矩阵A中,如果元素a;=a;,则称A为对称矩阵。对称矩阵具有以下的特点:
(1).对称矩阵中的元素关于主对角线对称,所以在存储矩阵时只需存上三角或下三角中元素,上下三角区中两个对称的元素共享一个存储空间。
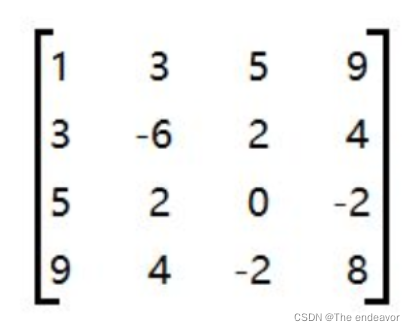
(2)假定“按行优先”存储主对角线以下(包括主对角线)的元素,第i行(1≤i≤n)有i个元素,元素总数为: n x (n+1)/2 (n为总行数)
因此,在存储矩阵时一般将这些元素存放在一个一维数组sa[0…n(n+ 1)/2- 1]中,但是必须要将矩阵的元素aij和一维数组的元素sa[k]对应起来,需要建立一个对应关系:
k = i x (i-1)/2 + j-1 (i >= j)
若i<j,则a;是上三角中的元素,因为a;=aj;,这样,访问上三角中的元素a;时则去访问和它对应的下三角中的aji即可,因此将上式中的行列下标交换就是上三角中的元素在sa中的对应关系:
k=j x (j- 1)/2 + i-1 (i <= j)
2.2 三角矩阵
三角矩阵分为上三角矩阵和下三角矩阵。上三角矩阵和下三角矩阵(不包括主对角线)中的元素均为常数C;下三角矩阵正好向相反,其上三角中的元素均为u常数C。因此,三角中的重复元素C 。可以共同共用一个存储空间;
其元素总数为: n x (n +1 )/2 (n为总行数)
因此,三角矩阵可以压缩存储在一维数组sa[ 0 … n(n+1)/2 ],常量C存储在sa数组中最后一个空间。同样的,要为矩阵的元素aij 和 一维数组元素 sa[k] 建立一个对立关系;
在上三角中的关系为:
a. 若 i <= j : k = ( i – 1) x (2n – i + 2)/2 + j – i
b. 若 i > j ; k = n x (n+1) / 2
在下三角中的关系为:
a. 若 i <= j : k = i x ( i – 1 ) / 2 + j – i
b. 若 i > j :k = n x (n+1) / 2
2.3 稀疏矩阵
假设矩阵A中有s个非零元素,如果
s远远小于矩阵元素的总数
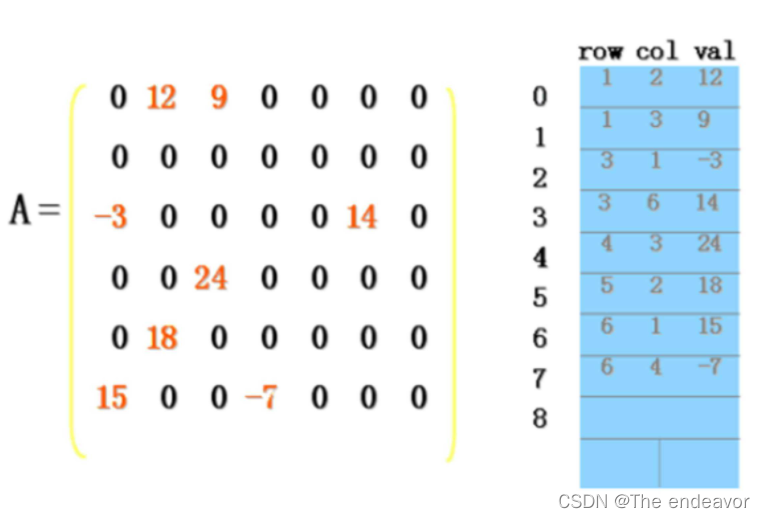
,则称A为稀疏矩阵,如图4-6所示。这种矩阵有一大半元素都是0,如果全部存储就太浪费空间,我们只需要存储非零元素即可。但是因为非零元素的分布没有规律,无法设定对应关系k,所以在存储元素时还必须存储其所在行号、列号,这就是三元组(i,j,v)。
注意:一般稀疏程度 e < 5% (相当于20个元素中,只有一个元素的矩阵)
三元组表
三元组类似于线性表中的线性表中的存储的结构体的类型,所以可以按照顺序表的定义方式来定义三元组,这种按顺序存储的稀疏矩阵称为三元组表;
如图:
稀疏矩阵代码参考:
#include <iostream>
#include <stdlib.h>
using namespace std;
#define TRIADSIZE 100
#define M 3
#define N 4
typedef int ElemType;
struct Triad
{
int i, j;
ElemType v;
};
typedef struct
{
Triad data[TRIADSIZE];
int m, n, k;
}SqTriadTable;
void CreateSqTriadTable(SqTriadTable* T, ElemType A[M][N])
{
int i, j, k = 0;
for (i = 0; i < M; i++)
{
for (j = 0; j < N; j++)
{
if (A[i][j] != 0)
{
T->data[k].i = i;
T->data[k].j = j;
T->data[k].v = A[i][j];
k++;
}
}
}
T->m = M;
T->n = N;
T->k = k;
}
void main()
{
SqTriadTable* T;
ElemType A[M][N];
int i, j, m;
T = (SqTriadTable*)malloc(sizeof(SqTriadTable));
cout << "请依次输入" << M << "X" << N << "的稀疏矩阵的值(并用空格隔开,回车换行)" << endl;
for (i = 0; i < M; i++)
{
for (j = 0; j < N; j++)
{
cin >> A[i][j];
}
}
CreateSqTriadTable(T ,A);
cout << "三维数组为:" << endl;
for (m = 0; m < T->k; m++)
{
cout << T->data[m].i;
cout << T->data[m].j,
cout << T->data[m].v;
cout << endl;
}
}
2.4 广义表
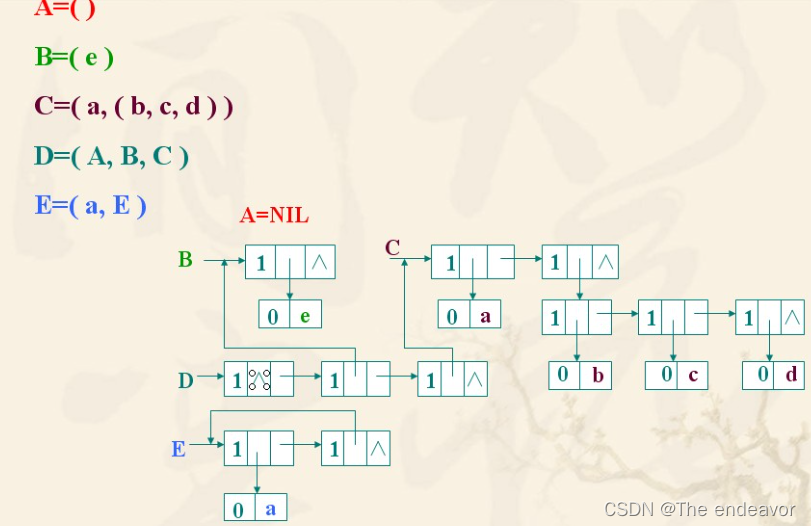
广义表(Lists.又称列表)是线性表的推广。在第三章中,我们把线性表定义为n >= 0 个元素 a1.a2.a3…an 的有限序列,性表的元素仅限于原子项,原子是作为结构上不可分割成分,它可以是一个数或一个结构,若放松对表元素的这种限制,容许它们具有其自身结构,这样就产生了广义表的概念。
广义表是n(n≥0)个元素a,a2 …an 的有限序列,其中 ai 或者是原子项,或者是一个广义表,通常记作LS=(a1, a2, a3 ,…an ) 。LS是广义表的名字,n为它的长度,若ai 是广义表,则称它为LS的子表。下面通过几个例子阐述广义表。
D=( ):空表,其长度为零。
A=(a,(b,)):表长度为2的广义表,其中第一个元素是单个数据a,第二个元素是一个子表(b,c)。
B=(A,A,D):长度为3的广义表,其前两个元素为表A,第三个元素为空表D。
C=(a,C):长度为2递归定义的广义表,C相当于无穷表C=(a,(a,(a,(…))))。
从以上的例子可以看出广义表具有以下特性:
(1)广义表的元素可以是子表,而子表还可以是子表,因此,广义表是一个多层的结构。
(2)广义表可以被其他广义表共享,如广义表B就共享A。在表B中不必列出表A的内容,只要通过子表的名称就可以引用该表。
(3)广义表具有递归性,如广义表C。