方法一:计算器法(最实用的方法)
方法二:二分法.在此不多累赘描述.
方法三:九章算术
1.从个位起向左每隔两位为一节,若带有小数从小数点起向右每隔两位一节,用“,”号将各节分开;
2.求不大于左边第一节数的完全平方数,为“商”;
3.从左边第一节数里减去求得的商,在它们的差的右边写上第二节数作为第一个余数;
4.把商乘以20,试除第一个余数,所得的最大整数作试商(如果这个最大整数大于或等于10,就用9或8作试商);
5.用商乘以20加上试商再乘以试商。如果所得的积小于或等于余数,就把这个试商写在商后面,作为新商;如果所得的积大于余数,就把试商逐次减小再试,直到积小于或等于余数为止;
6.用同样的方法,继续求。
有一幅示意图如下:
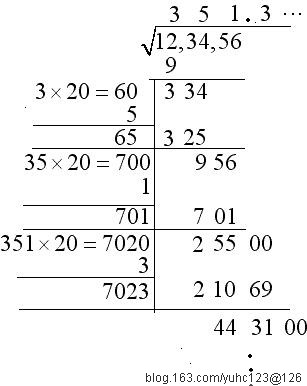
方法四:无穷级数(x是被开方数)
利用无穷级数可以得出多个根号运算公式.
无穷级数要用到泰勒定理,而泰勒定理需要拉格朗日定理的基础.所以,这里就直接给出一些由马克劳林公式求出的函数的泰勒公式.
(1)f(x)=ex
![]()
(2)f(x)=sinx
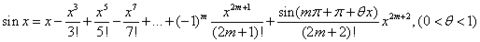
(3)f(x)=cosx
![]()
(4)

由(1),我们可以用t=Sqrt(x)来代x,消参后得到t和x的关系式.过程较为繁琐.
由(2)(3),我们可无从下手.
这时我们可以换一种思路,由(1)出发,不妨按推导(1)的方式,将e代为x,原指数x最终代为1/2,那么即可得到Sqrt(x)的值.而利用(4)中的(1+x)^m的展开式,我们可以直接求得:
Sqrt(2)=(1+1)^(1/2)=(1+x)^(1/2)=+1/2-(1/8)*(1/2)^2+(3/48)*1^3-…………
由右边等式求出(1+x)/0.5.
方法五:牛顿迭代法
设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0)+f'(x0)(x-x0),求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。重复以上过程,得r的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r的n+1次近似值,上式称为牛顿迭代公式.
所以我们可以设欲求根号的数为a,取初值x,使用x(n+1)=(x(n)+a/x(n))/2,迭代可得到解.
如a=2时,
(2/1+1)/2=1.5
(2/1.5+1.5)/2=1.416666666666666666666666666666….
(2/1.416666666666666666666666666666..+1.416666666666666666666666666666…)/2=1.414215686274509803921568627451…
三步就能得到5位精确数字,效率还是很高的,比较适合考试时用,
六:手算开n次方根
1、把被开方的整数部分从个位起向左每隔n位为一段,把开方的小数部分从小数点第一位起向由每隔n位为一段,用撇号分开;
2、根据左边第一段里的数,求得开n次算术根的最高位上的数,假设这个数为a;
3、从第一段的数减去求得的最高位上数的n次方,在它们的差的右边写上第二段数作为第一个余数;
4、把n(10a)^(n-1)去除第一个余数,所得的整数部分试商(如果这个最大整数大于或等于10,就用9做试商);
5、设试商为b。如果(10a+b)^n-(10a)^n小于或等于余数,这个试商就是n次算术根的第二位;如果(10a+b)^n-(10a)^n大于余数,就把试商逐次减1再试,直到(10a+b)^n-(10a)^n小于或等于余数为止。
6、用同样的方法,继续求n次算术跟的其它各位上的数(如果已经算了k位数数字,则a要取为全部k位数字)。
比如求987654321987654321的五次算术根,就算到小数点后四位。
3 9 7 1. 1 9 2 9
5√987’65432’19876’54321.00000’00000’00000’00000
243
________________________________________________
744 65432………………………………..74465432/(5×30^4)整数部分是18,用9作试商
659 24199………………………………..39^5-30^5
_____________________________________________
85 41233 19876…………………………..854123319876/(5×390^4)的整数部分是7,用7作试商
83 92970 61757…………………………..397^5-390^5
____________________________________________
1 48262 58119 54321……………………..1482625811954321/(5×3970^4)的整数部分是1,用1作试商
1 24265 57094 08851……………………..3971^5-3970^5
___________________________________________
23997 01025 45470 00000………………..23997010254547000000/(5×39710^4)的整数部分是1,用1作试商
12433 44352 06091 99551………………..39711^5-39710^5
_________________________________________
11563 56673 39378 00449 00000…………..1156356673393780044900000/(5×397110^4)的整数部分是9,用9作试商
11191 17001 57043 20516 21599…………..397119^5-397110^5
_________________________________________
372 39671 82334 79932 78401 00000……..3723967182334799327840100000/(5×3971190^4)的整数部分是2,用2作试商
248 70419 01386 56554 83574 43232……..3971192^5-3971190^5
_______________________________________
123 69252 80948 23377 94826 56768 00000..123692528094823377948265676800000/(5×39711920^4)的整数部分是9,用9作试商
111 91704 90192 14028 71518 74119 30649..39711929^5-39711920^5
_______________________________________
11 77547 90756 09349 23307 82648 69351
这样就得到987654321987654321的五次算术根精确到小数点前四位为3971.1929。
又如:
我们求 2301781.9823406 的5次方根:
第1步:将被开方的数以小数点为中心,向两边每隔n位分段(下面用’表示);不足部分在两端用0补齐;
23’01781.98234’06000’00000’00000’……….
从高位段向低位段逐段做如下工作:
初值a=0,差c=23(最高段)
第2步:找b,条件:(10*a+b)^n-(10*a)^n<=c,即b^5<=23,且为最大值;显然b=1
差c=23-b^5=22,与下一段合成,
c=c*10^n+下一段=22*10^5+01781=2201781
第3步:a=1(计算机语言赋值语句写作a=10*a+b),找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:(10+b)^5-10^5<=2201781,
b取最大值8,差c=412213,与下一段合成,
c=c*10^5+下一段=412213*10^5+98234=41221398234
第4步:a=18,找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:(180+b)^5-180^5<=41221398234,
b取最大值7
说明:这里可使用近似公式估算b的值:
当10*a>>b时,(10*a+b)^n-(10*a)^n≈n*(10*a)^(n-1)*b,即:
b≈41221398234/n/(10*a)^(n-1)=41221398234/5/180^4≈7.85,取b=7
以下各步都更加可以使用此近似公式估算b之值
差c=1508808527;与下一段合成,
c=c*10^5+下一段=1508808527*10^5+06000=150880852706000
第5步:a=187,找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:
(1870+b)^5-1870^5<=150880852706000,
b取最大值2,差c=28335908584368;与下一段合成,
c=c*10^5+下一段=2833590858436800000
第6步:a=1872,找下一个b,
条件:(10*a+b)^n-(10*a)^n<=c,即:
(18720+b)^5-18720^5<=2833590858436800000,
b取最大值4,差c=376399557145381376;与下一段合成,
c=c*10^5+下一段=37639955714538137600000
………………………..
最后结果为:18.724
原文链接:
http://blog.163.com/yuhc123@126/blog/static/3982949720083455020141/#