提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
1.离散型的dijkstra。
2.稠密型的dijkstra。
前言
关于dijkstra的一些体会与见解
一、
什么是dijkstra?
dijkstra是图论中的一种算法,用于在
有向图
,且当
每条边权重均非负
且没有最大边要求时,求出第n号点到第1号点的最短路径。
dijkstra的基本思想是用一个指针,依次从第一号点开始遍历,并且每次遍历过程均用该点来更新其余所有被该点相连的点,到起始处的距离。
比如下面的样例
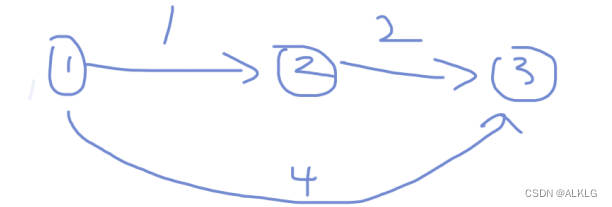
1号点到2号点距离是1;
2号点到3号点距离是2;
1号点到3号点距离是4。
显然,3号点到1号点最短路径是1→2→3,距离最小值为3,那么dijkstra算法实现这个答案的步骤是什么呢?
我们不妨给出一个数组dist[n],用来表示从1号点开始,每个点到起点的距离。起点设为点1。
初始时,我们将每个点距离起点的长度记作0x3f(我们可以将这个数视作正无穷),然后,再用dijkstra算法来更新。
初始化的代码操作如下:
#include <cstring>
memset(dist,0x3f,sizeof(dist));现在,让我们用dijkstra算法来模拟样例的过程:
初始化:
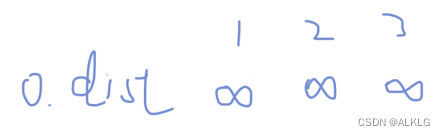
即第0次寻找,这时指针并未移动,所有点的最短路径都是∞。然后起点定为1号点,指针移向点1。

指针指向1之后,我们发现1号点存在:1→2,1→3两条有向线段,且长度分别为1,4。此时,比如,我们发现2号点到起点的距离原本是∞,可是∞小于1号点到2号点的距离(
就是1
)加上1号点到起点的距离(
就是0
),所以,二号点到起点的距离我们就能将它更新成
1,
三号点同理。

然后指针继续移动到2,此时对于3号点,我们发现由2号点到3号点的距离(
就是2
)加上2号点到起始处的距离(
就是1
)小于原本3号点到起点的距离(
就是4
),由此,我们才算将3号点到起点,即1号点的最短路径更新成了3,而不是原来的4,至此,上述样例的dijkstra模拟过程完美结束。
二、dijkstra的几种类型
1.离散型的dijkstra:
对于离散型的dijkstra,一般用邻接矩阵来存储,什么是离散型的dijkstra呢?一般图中边数m是点数n的平方的都可视作离散型的图。
例:
给定一个n个点m条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出1号点到 n 号点的最短距离,如果无法从1号点走到n号点,则输出 −1。
题目来源:
849. Dijkstra求最短路 I – AcWing题库
1.如何用邻接矩阵存储图:
#include <iostream>
#include <cstring>
#include <algorithm>
const int N = 510;
int g[N][N];//邻接矩阵可以看成二维数组,g[a][b]表示点a到点b的距离。
int n,m;//n个点,m条边。
int main(){
cin >> n >> m;
memset(g,0x3f,sizeof(g));
while(m--){
int a,b,c;
cin >> a >> b >> c;//输入a,b两个点,c为a,b距离。
g[a][b] = min(g[a][b],c)//初始化。
}
return 0;
}
2.dijkstra算法实现:
int g[N][N];
int dis[N];
int n,m;
bool st[N];
int dijkstra(){
memset(dis,0x3f,sizeof dis);
dis[1] = 0;
for(int i = 0;i < n-1;i++){
int t = -1;//取未被标记最近点。
for(int j = 1;j <= n;j++)
if(!st[j] && (t == -1 || dis[t] > dis[j]))
t = j;//指针未开始移动或者,此时点距起点距离更小,并且指针没移到过该点。
for(int j = 1;j <= n;j++){
dis[j] = min(dis[j],dis[t] + g[t][j]);//更新距离
}
st[t] = true;//标记
}
if(dis[n] == 0x3f3f3f3f)return -1;//如果值仍然是无穷则说明不存在最小值。或者1号点无法到达n号点。
return dis[n];
}完整代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int g[N][N];
int dis[N];
int n,m;
bool st[N];
int dijkstra(){
memset(dis,0x3f,sizeof dis);
dis[1] = 0;
for(int i = 0;i < n-1;i++){
int t = -1;
for(int j = 1;j <= n;j++)
if(!st[j] && (t == -1 || dis[t] > dis[j]))
t = j;
for(int j = 1;j <= n;j++){
dis[j] = min(dis[j],dis[t] + g[t][j]);
}
st[t] = true;
}
if(dis[n] == 0x3f3f3f3f)return -1;
return dis[n];
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m;
memset(g,0x3f,sizeof g);
while( m-- ){
int x,y,z;
cin >> x >> y >> z;
g[x][y] = min(g[x][y],z);
}
cout << dijkstra() << endl;
return 0;
}
2.稠密型的dijkstra
当边数m << 点数n^2时,用邻接表存。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e6 + 10;
typedef pair<int,int> PII;//first存距离,second存坐标
int n,m,h[N],e[N],ne[N],idx;
int dist[N],w[N];
bool st[N];
void add(int a,int b,int c){
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}//邻接表
int dijkstra(){
memset(dist,0x3f,sizeof(dist));//初始化
dist[1] = 0;
priority_queue<PII,vector<PII>,greater<PII>> heap;//定义小端堆
heap.push({0,1});
while(heap.size()){
auto t = heap.top();//取最小值
heap.pop();//去最小值
int ver = t.second,distance = t.first;
if(st[ver])continue;
st[ver] = true;
for(int i = h[ver];i != -1;i = ne[i]){
int j = e[i];
if(dist[j] > dist[ver] + w[i]){//更新
dist[j] = dist[ver] + w[i];
heap.push({dist[j],j});
}
}
}
if(dist[n] == 0x3f3f3f3f)return -1;
return dist[n];
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m;
memset(h,-1,sizeof(h));
while(m--){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
cout << dijkstra() << endl;
return 0;
}