博客

感谢谷歌大脑！这个

手册

系统的总结了调参的整个过程。

1.start point

从一个简单的模型入手，使用简单的优化器（比如固定了beta1,beta2,momentum的ADAMW优化器）。

1.1.确定batch_size：

不同的batch_size对训练结果没有影响。在不同的batch_size下可以通过调整优化器的参数（比如学习率，动量等）

实现相同的优化结果

。需要注意的是，在小的数据集（如MFNet数据集）上，实验中发现大的batch_size训练出的结果，过拟合更加明显。这个在这个手册中也有说明，小的batch_size（在使用shuffle data_loader）的情况下，由于是数据随机导入的原因，batch_size越小，在训练相同个epoch的情况下，其引入的随机性更强，也就是文中所说的引入噪声，因此起到正则化的作用（从某种角度上来看，也可以看成是数据增强的一种方式）。此外文中说到不建议使用梯度累积来模拟大的batch_size。对于这点，我是这么看的，在硬件资源受限的情况下，如果在一个硬件资源更强大的机器上已经调优了一个大batch_size的版本，此时，为了偷懒，可以使用梯度累加的策略。此时需要考虑的是，基础的batch_size 不能太小，否则梯度累积模拟的大的batch_size 和实际的大的batch_size 会有

比较明显的差异

（这种差异的可能原因和批处理的EMA统计有关)。总而言之，对于一个没有先验知识的模型，从头开始调试的话，batch_size的选择依据是，尽量可能大。至于怎么选，自己去试就是了。需要注意的是，每次重新选择batch_size都需要重新调整优化器参数，在参数都调好了的情况下，一个可以

参考的经验

是：

example：

我们使用

gmnet

模型作为我们的基础模型，优化器为adamW:

torch.optim.AdamW(parameter_group, betas=(0.9, 0.999), eps=1e-8, weight_decay=float(config['weight_decay']), amsgrad=True)

其中weight_decay为0.1

，数据集为

MFNet

。关闭梯度裁剪。直接使用混合精度计算。

学习率使用polinominal策略：

lr_policy: polynomial
power: 0.9
niter_decay: 200
lr_step_per_batch: False
cycle: False
end_lr: 1e-8
backbone_lr: 0.0005

batch size 分别设置成2,4,8,16，跑5个epoch，平均每轮的训练的时间分别为：133s,81s,42.25s,46.52s

可以看出，虽然硬件允许的最大batch size是16，但是不是最大的batch size就能够带来最快的训练速度。我们查看gpu消耗：

可以看到 batch size为16和8的情况下，gpu温度均超过60°，怀疑此时gpu进行了降频处理，性能下降。可以简单的认为，文中的结论存在的情况为，gpu没有接近其性能极限，比如：所占内存不超过gpu内存综合的70%。

综上我们选择batch size 为8作为我们的批大小（16的批大小不能带来运算效率的提升，但是可能让模型的泛化能力变差）

1.2.选择初始配置

使用简单的学习率衰减方案（比如直接使用固定的学习率），尽量少的变量能够有助于对问题有更加直接的认识。选择训练的总epoch数。

2.增量调优

从一个简单的基础设置开始，比如说恒定的学习率，固定参数的adamw优化器，基础简单的网络架构。然后慢慢的加特征，比如说增加学习率衰减策略，调优adamw的beta1，beta2，momentum等参数。增加网络模块等。

3.探索式调优和针对性调优

原文是Exploration vs exploitation，这里说说我的理解，我们在初次遇到一个问题的时候。我们对问题的认识往往是不充分的，比如

• 是否引入新的技巧（比如如果存在过拟合，则可以引入正则化技巧），
• 学习率合适的搜索范围是多少（如果确定错误的超参数范围，有可能让最优模型陷在一个错误的点，或者引入错误的模块），
• 确定对验证集误差（简称为验证误差）敏感的超参数（在每次消融实验的时候，都尽可能的去重新调优）和不敏感的超参数（在每次消融实验的时候，可以设置成固定参数，减少搜索空间）

探索阶段

则我们首先研究不同优化器的选择，SGD和ADAMW，对于优化器选择了SGD的实验，我们还需要确定学习率的大小，我们可以简单的使用固定学习率的策略，使用伪随机搜索的策略，确定学习率的大概范围，类似的我们可以确定动量的大概范围，weight_decay的范围，nestrov是否设置成False。在随机搜索的时候，我们可能发现过拟合的现象，因此我们添加了正则化，然后重新进行伪随机搜索确定优化器参数的范围，有可能的，我们还会发现我们的训练误差存在NAN的情况，此时我们就需要考虑使用合适的策略减少NAN的问题（利用学习率warm up或者使用梯度裁剪），然后我们还可以考虑选择合适的学习率衰减策略，针对不同的学习率衰减策略，进行不同的伪随机搜索。

针对性调优

在确定了以上问题之后，我们用贝叶斯优化器在选定的学习率范围内进行进一步的搜索，确定最终的优化结果。

尽可能的分析每次尝试的结果，包括验证集上的误差，训练误差，各种单项损失函数，梯度范数等。从数据中对调优问题获取更好的认知，比如是否存在过拟合，是否存在梯度爆炸，单项损失函数是否起到该有的作用等等。尽可能的获取有效分析，不能够被一次幸运训练的结果给误导（由于训练的随机性，有时候即使是错误的配置也可能踩狗屎地得到好结果），所有的结果都需要有经得起推敲的支撑。对于随机性的一种有效解决方案，是多做几次训练，分析多次的训练结果。如果不同结果之间存在比较大的偏差，则说明这次结果可能是狗屎运。需要剔除。

因此在做尝试性实验之前，需要制定好本次实验的目的，比如确定某一个超参数的作用，确定某一个模块的作用。需要注意的是，实验设计需要遵循单一变量原则。

4.科学的实验

确定scientific, nuisance, and fixed hyperparameters。科学参数是实验设计的目标，实验设计需要研究科学参数对问题的影响。冗余参数是每轮实验需要调优的参数，每次改变科学参数都需要重新调优冗余参数，否则对比实验是不合理的。固定参数是实验中固定的参数。

比如说做消融实验，要验证所提出的模块具有作用，需要对比添加该模块和无该模块下的效果。那么该模块是否存在就是科学参数，二对应的学习率，优化器参数，正则化参数，以及损失函数涉及的参数，就是冗余参数，每轮实验的数据都需要保证是调节冗余参数，获取了最有训练结果的前提下进行对比，否则实验就存在公平性争议。

5.确定实验目标

需要首先确认每个实验的目标。科学参数和冗余参数以及固定参数的确定都和实验目标相关，比如，对于实验目标为，确定适合的模型大小（比如选取不同的层数，宽度等），则其科学参数可以为模型的参数，而此时如果讲weight decay作为固定参数显然是不合适的，因为对不同模型大小，其最优的weight decay是不一样的。

优化器相关的参数，学习率，学习率的衰减策略，beta1，beta2，动量，weight decay等是冗余参数。

一些可以固定的参数：

1. 优化器的类型选择(SGD,ADAMW等）是一个科学参数或者固定参数，我们认为所有的优化器都可以得到最优的训练结果。所不同的是不同的优化器其训练的难易不一样。训练的时间长度不一样。
2. 是否添加某种正则化技巧（比如random_flip/crop/cut_out）等，是一个科学参数，或者是一个固定参数
3. 神经网络的结构相关的参数（如层数）往往是科学参数或者固定参数。

我们的实验目标是确定最优的优化器。SGD和ADAMW。则对应的SGD的调参（冗余参数）为：

learning_rate，weight decay，momentum，nesterov，dampening

ADAMW对应的冗余参数为：

learning_rate, weight decay, beta1, beta2, eps, amsgrad

我们将nestrov固定为True，将amsgrad固定为

False

6.设计研究（study）

研究是针对特定的科学参数，对冗余参数进行优化，从而让不同科学参数之间的对比尽可能的公平，因此研究的步骤包括：

1. 确定tunning变量（就是冗余变量）
2. 确定冗余变量的取值范围，即搜索空间
3. 确定进行tunning的次数（number of trials）
4. 利用伪随机搜索进行探索性尝试，确定指定的搜索范围是否合理。确定是否需要添加正则化等策略
5. 重复1~4，直到确定了1~3，并限制在一个比较合理的范围内。
6. 利用贝叶斯优化器进行迭代式优化，寻找最优的配置。

如果科学参数有多种取值，需要进行多次研究，在运算负载不够的情况下，一种可行的办法是将科学参数也和冗余参数一起，进行1~6的调优。

需要注意的是，在设计研究的时候，需要平衡硬件条件和搜索范围，搜索次数。越多科学参数的取值，越广的冗余参数的搜索范围，在搜索范围内越密集的采样能够得到更加让人信服的结果。然而也更加消耗计算资源和调参的时间。

7.数据分析

在分析所设计的实验是否取得预设的目标时（比如选取确定最优的优化器）。我们需要对训练得到的结果（包括过程数据）进行分析，避免错误的设计带来的问题。我们需要检查一下几个方面的问题：

7.1 搜索空间是否足够大

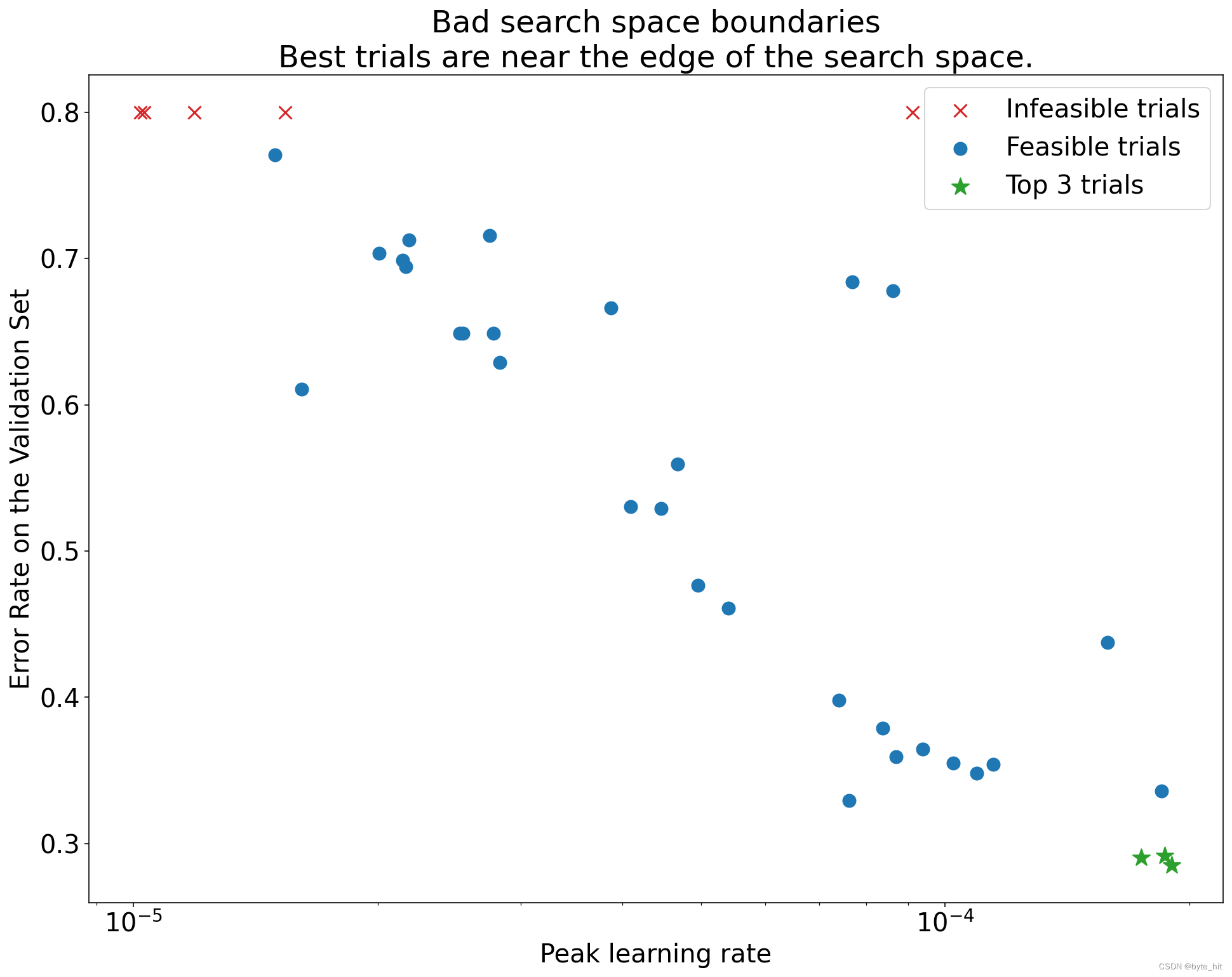
如上图（超参数轴图，纵轴为每次trial训练过程中得到的最优的验证集误差，横轴为具体某个超参数）所示，如果最优的点簇在搜索空间的边缘，此时扩展搜索空间，可能带来新的最优值。

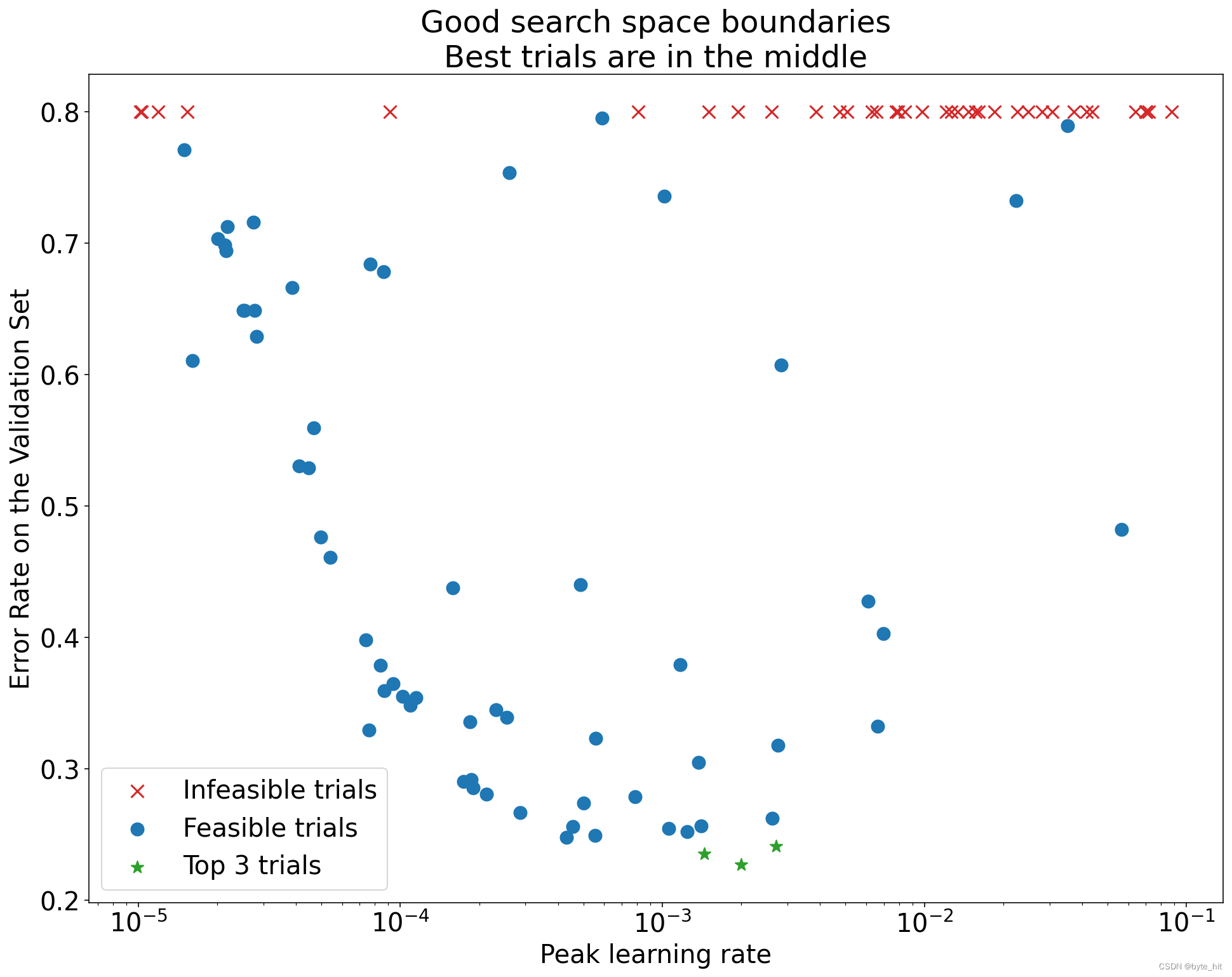
上图所示的结果，搜索空间是没有问题的，但是对于学习率大于最优点的区域存在大量的无效点，这说明可能存在不稳定问题，限制了大学习率下模型的表现。

7.2 是否已经在搜索空间在进行足够密集的采样

没有确切的准则用于判定是否进行了足够的采样，一种方案是在运算载荷能够承担的情况下，尽可能多的采集点，也就是在搜索空间中进行尽可能多的尝试（trials）。然后分析超参数轴图，最好的点簇中包含多少个点。一般来讲包含越多的点，越能够说明采样是足够稠密的。

7.3 每项研究中，有多少trials是无效的

如果尝试中损失函数发散，或者损失函数异常（很大或者nan），或者运行报错，我们称之为无效的训练。如果研究中，存在很大比例的无效尝试，则需要调整搜索空间，避开无效区域，或者检查代码是否存在bug。

7.4 模型是否存在优化问题《这个值得专门分一个章节来讲》

7.5 最优的trial的训练曲线是否存在过拟合等问题

训练曲线包含更加丰富的信息，对于每一个研究，我们至少需要查看其最优的几次尝试的训练曲线。如果训练曲线表明存在过拟合问题（随着训练step的增加，验证误差也逐渐增加）。除非研究对象就是正则化手段。否则需要考虑调整正则化参数或者添加正则化手段。除了最优的trial出现过拟合问题需要关注之外，如果存在以下问题，也说明最优的trial选择上可能存在问题：

• 如果最优的trial不存在过拟合，但是其他trial存在过拟合现象
• 需要考虑参数的合理性，比如，对于过拟合问题，如果学习率过低，也会降低过拟合问题，但是过低的学习率是不合理的。也就是说最优的trial选择有可能选取了那些比较差的科学参数或者冗余参数配置。

除了过拟合问题需要关注，我们也需要关注：

训练曲线中step-to-step（这里的step可以是训练中的一次迭代iteration或者一个epoch）方差

大的方差会导致复现困难，说明可能恰好最后一个是在lucky step上。大的方差的主要原因有

• 批之间差异（数据shuffle加载），小的批大小容易导致批之间存在比较大的差异
• 较小的验证集，验证集太小，验证集太小，其随机性越强，和训练集数据分布的差异更大
• 以及较大的学习率

针对step-to-step方差，相应的解决方案为，增加批大小，增加验证集，利用学习率衰减，或者使用移动平均对验证误差进行平滑处理。

训练过程中的尾声阶段，验证误差是否还下降

这说明还没有达到最优的训练结果。通过增加训练steps总数或者通过调整学习率策略来达到最优的验证误差。

训练结束之前，验证误差是否已经饱和（收敛）

可以减少训练的step数来节省运算开支

其他异常（比如训练误差发散）表明需要对代码进行debug

如果存在以上问题，需要解决了然后重新调优。如果没有存在以上的问题，则可以move on继续其他的研究。同时可以在代码中自动生成所有的训练曲线和超参数轴图。

8.再次确定所添加的更改（比如新的网络层，新的超参数设置）是否真的有效

由于神经网络训练存在随机性，我们貌似得到了很好的验证集结果。但是当我们使用同样的参数再次训练的时候。我们有时候会痛苦的发现，好运气用完了。始终无法复现之前好的实验结果。这种训练的差异主要分为：

1. 尝试（trial）差异：主要是因为不同trial的随机初始化，训练数据的随机加载，dropout mask的随机性，数据增强引入的随机性，并行算子的运算顺序等；
2. 超参搜索或者研究差异：比如在伪随机搜索算法中的随机种子不同，会导致最终采样的点不同
3. 数据采样差异：对数据集的随机划分，划分为训练数据集，测试数据集和验证数据集，进一步的在数据生成过程中的随机性也可能带来这种不一致。

手册里头说更关注的是研究差异，建议在搜索空间中采样足够多的点，以消除采样导致的研究差异。另外也可以直接在最好的超参数配置上，进行多次的重复训练，统计多次训练的偏差。在硬件计算负载能够承担得起的情况下，进行多次的训练，避免采用训练偏差大的改变是更加科学的。

9.探索之后

其实就是说进行探索式调优之后，怎么进行针对性的调优，相当于在探索调优确定的超参数搜索范围内更加精细，密集的搜索最优的配置。这个阶段不用伪随机搜索算法，而是使用贝叶斯优化。如果搜索空间中包含大量的不可行点。建议使用黑盒优化工具进行优化。

此时我们也需要考虑在测试数据集上的表现。

10.确定训练的步长

11.关于软件使用

手册中建议使用ossVizier进行参数搜索。我也整理了

相关的资料

。折腾这么多天，个人的感受是，用来做quasi_random确定初步的范围还可以，但是每次用高斯过程来优化的时候。总会碰到训练轮次偏差过大的问题。或许是训练样本过小导致的每个轮次的差异性比较大导致的吧。