19180 集合划分问题
时间限制:1000MS 代码长度限制:10KB
提交次数:0 通过次数:0

题型: 编程题 语言: G++;GCC;VC;JAVA
Description
教材课后习题2-8
n个元素的集合{1,2,…,n}可以划分若干个非空子集。例如,当n=4时,集合{1,2,3,4}可以划分为15个不同的非空子集如下:
{
{1},{2},{3},{4}},
{
{1,2},{3},{4}},
{
{1,3},{2},{4}},
{
{1,4},{2},{3}},
{
{2,3},{1},{4}},
{
{2,4},{1},{3}},
{
{3,4},{1},{2}},
{
{1,2},{3,4}},
{
{1,3},{2,4}},
{
{1,4},{2,3}},
{
{1,2,3},{4}},
{
{1,2,4},{3}},
{
{1,3,4},{2}},
{
{2,3,4},{1}},
{
{1,2,3,4}}
给定正整数n(1<=n<=20),计算出n个元素的集合{1,2,…,n} 可以化为多少个由m个不同的非空子集组成的集合。
输入格式
两个整数n和m。
输出格式
集合划分的数量。
注意此类问题数据较大,需要使用long long 类型。
输入样例
4 3
输出样例
6
解题思路
递归
找规律
递归思路:以最大数n为例
-
n
独立作为一个子集
,问题就演变为 n – 1 个数分为 m – 1 个集合。即:如果现在是将4个元素划分为3个集合,如果加入第四个数时要求为独立一个子集,那在这基础上,结果加上个数为3个元素划分为2个集合的数量。 - n 和其他数字在一起构成子集,那么先将 n – 1 个数字分为 m 个集合,再将 n 插入到这 m 个集合中的某个集合中去,因此此时会有 m 种插入方案。
举例
以集合元素个数为4为例,我们来看应该怎么求解集合划分问题。因为我们采用的是分治策略,因此,我们先看集合元素个数为3的集合的划分
考虑3个元素的集合,可划分为
-
1个子集的集合:{
{1,2,3}} -
2个子集的集合:{
{1,2},{3}},{
{1,3},{2}},{
{2,3},{1}} -
3个子集的集合:{
{1},{2},{3}}
因此 F(3, 1) = 1; F(3, 2) = 3; F(3, 3) = 1;
如果我们要求4个元素的集合划分为2个子集的集合的个数F(4,2),求解过程如下:
-
如果这第4个元素不是独立子集,因此在2个子集的集合中加入4,加入4的方式如下:
{
{1,2,4},{3}},{
{1,2},{3,4}},
{
{1,3,4},{2}},{
{1,3},{2,4}},
{
{2,3,4},{1}},{
{2,3},{1,4}}
即如果有 m 个子集,那么该情况的个数为 m * F(n – 1, m)
-
如果这第4个元素作为独立子集,只有一种方式
{
{1,2,3},{4}}
即在 F(n – 1, m – 1) * 1
所以:F(4, 2)= 2 * F(3, 2)+ F(3, 1)
由以上的演示可以得出集合划分的公式如下:
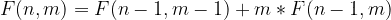
此式中n为元素个数,m为子集个数。
递归终止条件
- 可划分为的集合数为1时,即不能再少了;
- 当 n == m,即元素和集合个数相等时,比如6个元素划分为4个,只能递归至4个元素划分为4个集合,而不能继续递归成3个元素划分为4个集合了(此时会出现空集合,而题目要保证每个集合至少一个元素)。
算法思路
更多注释可查看下方的完整代码中,有助于理解
代码如下
#include <iostream>
using namespace std;
/*
20 10
5917584964655
*/
long long f(int n,int m)
{
// 递归结束条件,n和m相等,即此时每个集合只有一个元素,因为比如4个元素最多只能划分为4个集合,或只划分为1个集合
if(n == m || m == 1) {
return 1;
} else {
return f(n - 1, m - 1) + m * f(n - 1, m);
}
}
int main()
{
int n, m;
cin >> n >> m;
cout << f(n, m) << endl;
return 0;
}
最后
对我感兴趣的小伙伴可查看以下链接
-
我的掘金主页:
https://juejin.cn/user/1302297507801358
-
博客主页:
http://blog.zhangjiancong.top/
- 公众号:Smooth前端成长记录