博客

双线性插值

原理

：

那么对于浮点数的坐标(x,y)满足(a<=x<a+1,b<=y<b+1)，我们可以先分别求出c(x,b)和c(x,b+1):

c(x,b) = c[a+1][b]

(x-a)+c[a][b]

(1+a-x);

c(x,b+1) = c[a+1][b+1]

(x-a)+c[a][b+1]

(1+a-x);

好，现在已经知道c(x,b)和c(x,b+1)了，而根据假设c(x,b)到c(x,b+1)也是线性变化的，所以:

c(x,y) = c(x,b+1)

(y-b)+c(x,b)

(1+b-y)

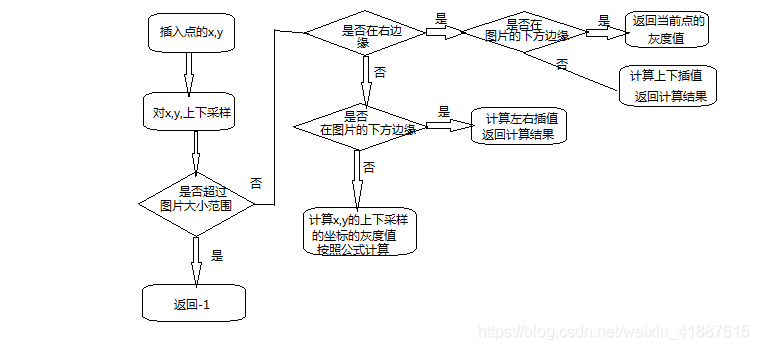
代码

：

//双线性差值
int InterpBilinear(const QImage &image,double x,double y)
{
    int width = image.width();
    int height = image.height();

    //四个临近点的坐标 (x1,y1)、(x1,y2),(x2,y1)，(x2,y2)
    int x1,x2;
    int y1,y2;

    //两个差值的中值
    double f12,f34;
    double	epsilon = 0.0001;

    //四个临近像素坐标x像素值
    double f1,f2,f3,f4;

    //计算四个临近坐标
    x1 = (int)x;
    x2 = x1 + 1;
    y1 = (int)y;
    y2 = y1+1;

    //不在图片的范围内
    if((x < 0) || (x > width - 1) || (y < 0) || (y > height - 1))
    {
        return -1;
    }else{
        if(fabs(x - width+1)<=epsilon) //如果计算点在右测边缘
        {
            //如果差值点在图像的最右下角
            if(fabs(y - height+1)<=epsilon)
            {
                f1 = qGray(image.pixel(x1,y1));
                return f1;
            }else {
                f1 = qGray(image.pixel(x1,y1));
                f3 = qGray(image.pixel(x1,y2));

                //图像右方的插值
                return ((int) (f1 + (y-y1)*(f3-f1)));
            }
        }
        //如果插入点在图像的下方
        else if(fabs(y - height+1)<=epsilon){
           f1 = qGray(image.pixel(x1,y1));
           f2 = qGray(image.pixel(x2,y1));

           //图像下方的插值
           return ((int) (f1 + (x-x1)*(f2-f1)));
        }
        else {
            //得计算四个临近点像素值
            f1 = qGray(image.pixel(x1,y1));
            f2 = qGray(image.pixel(x2,y1));
            f3 = qGray(image.pixel(x1,y2));
            f4 = qGray(image.pixel(x2,y2));

            //第一次插值
            f12 = f1 + (x-x1)*(f2-f1); //f(x,0)

            //第二次插值
            f34 = f3 + (x-x1)*(f4-f3); //f(x,1)

            //最终插值
            return ((int) (f12 + (y-y1)*(f34-f12)));
        }
    }

}