常见分布
总结统计工作中几个常用用法在python统计函数库scipy.stats的使用范例
常见术语
-
pdf
,概率密度函数(Probability Density Function),连续型随机变量的概率。 -
cdf
,累积分布函数(Cumulative Distribution Function),pdf的积分。 -
ppf
,百分点函数(Percent Point Function),cdf的逆函数。 -
pmf
,概率质量函数(Probability Mass Function),离散型随机变量的概率。 - sf,残存函数(Survival function),它的值为(1-CDF)
- isf,逆残存函数(Inverse survival function),sf的逆函数
常见随机分布
| 名称 | 含义 |
|---|---|
| uniform | 均匀分布 |
| norm | 正态分布 |
| t | 学生T分布 |
| f | F分布 |
| poisson | 泊松分布 |
| bernoulli | 伯努利分布 |
| binom | 二项分布 |
| expon | 指数分布 |
| chi2 | 卡方分布 |
下面我们以正态分布(Norm)和泊松分布(Poisson)为例做详细的介绍
1.正态分布(Norm)
norm = scipy.stats.norm(loc=0, scale=1)
正态分布,属于连续性概率分布函数,
loc
表示均值,
scale
表示标准差。其概率密度函数为:
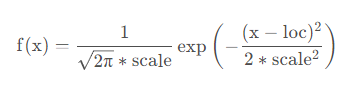
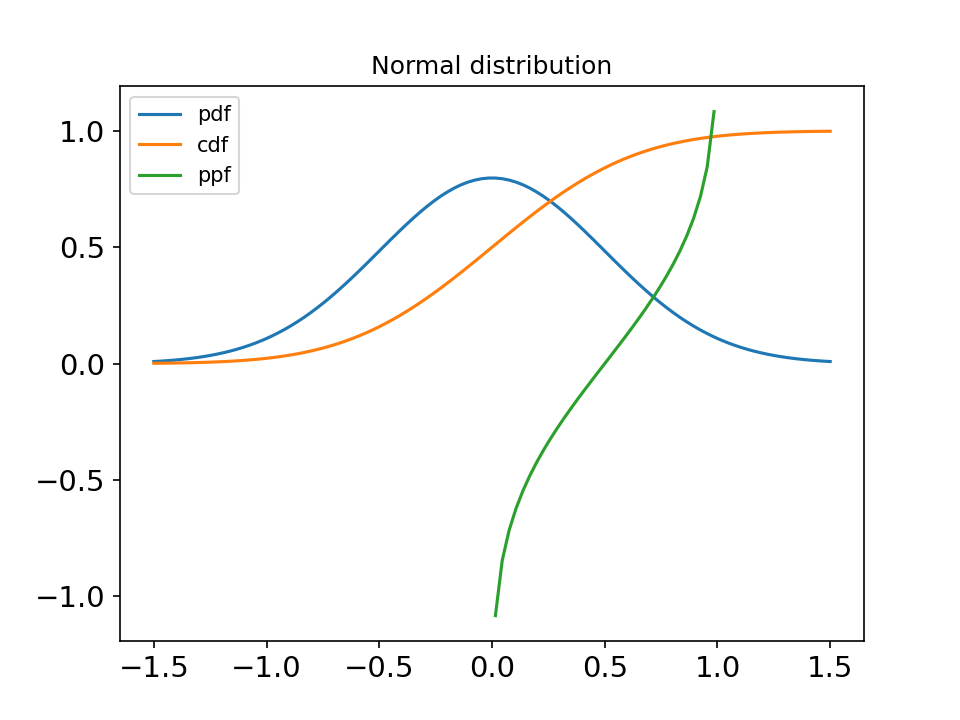
x = np.linspace(-1.5, 1.5, 100)
labels = []
f_list = [stats.norm.pdf, stats.norm.cdf, stats.norm.ppf]
plt.figure(dpi=150)
for f in f_list:
labels.append(f)
y = f(x, loc=0, scale=0.5) #标准正态分布,均值0,标准差0.5
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)
plt.legend(labels=['pdf', 'cdf', 'ppf'], loc='best')
plt.title("Normal distribution")
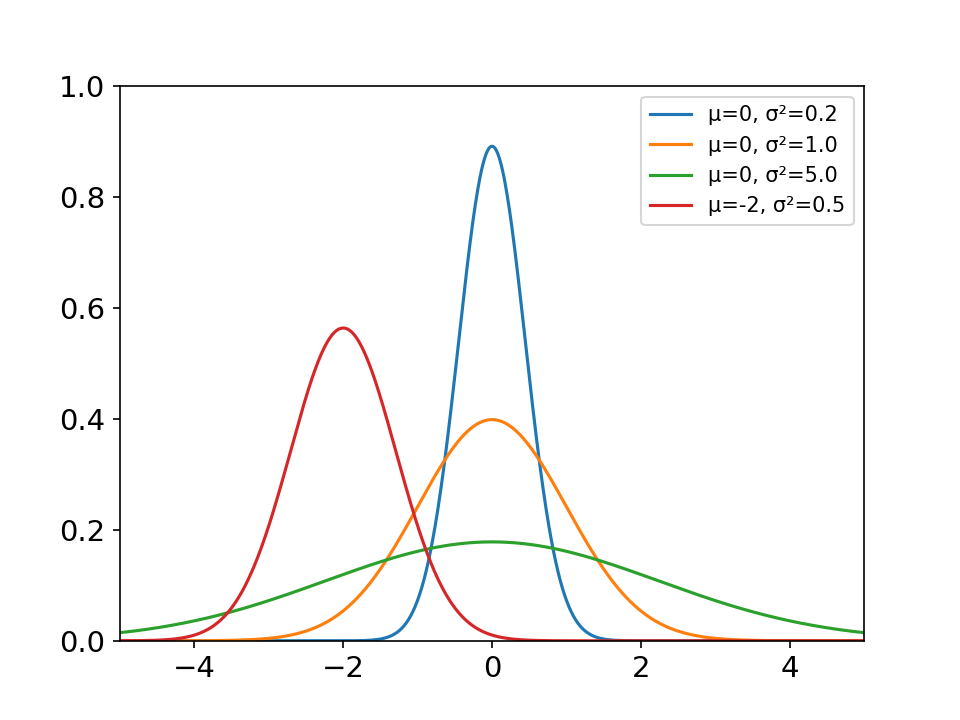
import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np
import math
x = np.linspace(-5, 5, 1000)
labels = []
mu_list = [0, 0, 0, -2]
sigma_list = [0.2, 1.0, 5.0, 0.5]
plt.figure(dpi=150)
for mu, sigma in zip(mu_list, sigma_list):
labels.append('μ={}, σ²={}'.format(mu, sigma))
y = stats.norm.pdf(x, loc=mu, scale=math.sqrt(sigma))
plt.axis([-5, 5, 0, 1.0])
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)
plt.legend(labels=labels, loc='best')
plt.show()
连续随机变量对象的方法
rvs:产生服从这种分布的一个样本,对随机变量进行随机取值,可以通过size参数指定输出的数组大小。
from scipy import stats
rv_norm=stats.norm.rvs(loc = 5,scale = 1,size =(2,2))
# array([[4.75695311, 5.71218072], [6.05233184, 5.56499171]])
rv_norm=stats.norm.rvs(loc = 5,scale = 1,size =6)
# array([3.39791064, 5.18353263, 2.38873254, 5.00970607, 4.36979662, 4.16425798])
pdf:随机变量的概率密度函数。产生对应x的这种分布的y值
# 比如我们想知道标准正态分布得到0的概率。
st.norm.pdf(x=0,loc=0,scale=1)
0.3989422804014327
cdf:随机变量的累积分布函数,它是概率密度函数的积分(也就是x时p(X<x)的概率)。产生对应x的这种分布的累积分布函数的值。
x=st.norm.cdf(0.842,loc=0,scale=1)
y=st.norm.cdf(1.6449,loc=0,scale=1)
z=st.norm.cdf(2.33,loc=0,scale=1)
print(x,y,z)
0.8001060232739432 0.9500047825316537 0.9900969244408357
问题:正态分布的3σ原则为:数值分布在(μ-σ,μ+σ)中的概率为0.6827;数值分布在(μ-2σ,μ+2σ)中的概率为0.9545;数值分布在(μ-3σ,μ+3σ)中的概率为0.9973,可以认为,Y的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%。
证明如下:
x=st.norm.cdf(1,loc=0,scale=1)
y=st.norm.cdf(2,loc=0,scale=1)
z=st.norm.cdf(3,loc=0,scale=1)
print(x-(1-x),y-(1-y),z-(1-z))
0.6826894921370859 0.9544997361036416 0.9973002039367398
ppf:累积分布函数的反函数。q=0.01时,ppf就是p(X<x)=0.01时的x值。
inv_z095=st.norm.ppf(0.95)
inv_z099=st.norm.ppf(0.99)
inv_z080=st.norm.ppf(0.80)
print(inv_z080,inv_z095,inv_z099)
0.8416212335729143 1.6448536269514722 2.3263478740408408
interval:中位数周围面积相等的置信区间
# 证明数值分布在(μ-2σ,μ+2σ)中的概率为0.9545
interval=st.norm.interval(0.9544997361036416,loc=0,scale=1)
interval
Out[56]: (-2.0000000000000004, 2.0000000000000004)
st.norm.interval(0.95,loc=0,scale=1)
Out[57]: (-1.959963984540054, 1.959963984540054) # 1.96
fit:对一组随机取样进行拟合,找出最适合取样数据的概率密度函数的系数。如stats.norm.fit(x)就是将x看成是某个norm分布的抽样,求出其最好的拟合参数(mean, std)连续分布函数特有方法
import numpy as np
from scipy import stats
data = stats.norm.rvs(size=1000, random_state=3) # 生成随机数
print(np.mean(data), np.std(data))
print(stats.norm.fit(data))
0.017284332980834295 1.0084018990512724
(0.017284332980834295, 1.0084018990512724)
泊松分布(Poisson)
首先要清楚,泊松分布是离散的,也就是说我接到骚扰电话次数必须是整数,要么就是15次,要么就是16次…,而不会是15.5次。

均值方差:泊松分布的均值和方差都是 λ。
使用poisson.rvs(mu, size) 函数生成服从泊松分布数据,给定均值和样本大小:
from scipy import stats
data = stats.poisson.rvs(mu=2, size=10, random_state=5343)
# data
# array([2, 0, 3, 1, 1, 2, 3, 3, 4, 1], dtype=int64)
泊松分布属于离散型概率分布函数, 其概率质量函数为poisson.pmf(k, mu)
上述概率质量函数以“标准化”形式定义。要移动分布,请使用loc参数。具体来说,就是泊松pmf(k,mu,loc)等同于泊松。pmf(k-loc,mu)
# 某商店每天平均有三位顾客,某天恰好有5人的概率:
from scipy.stats import poisson
poisson.pmf(k=5, mu=3)
# 结果为 0.100819
使用poisson.cdf(k, mu)及计算泊松分布的累积分布函数值
# 某商店平均每天卖7个足球,那么某天卖出足球数量小于5的概率:
from scipy.stats import poisson
# 计算累积概率
poisson.cdf(k=4, mu=7)
# 结果为 0.172992
# 某商店平均每天卖15个罐头,则某天卖出罐头超过20听的概率:
# 1减去累积概率
1-poisson.cdf(k=20, mu=15)
# 结果为 0.082971
poisson.ppf(q, mu, loc=0)累积分布函数的反函数
stats.poisson.ppf(q=0.95, mu=3, loc=0)
Out[58]: 6.0
stats.poisson.ppf(q=0.95, mu=5, loc=0)
Out[59]: 9.0
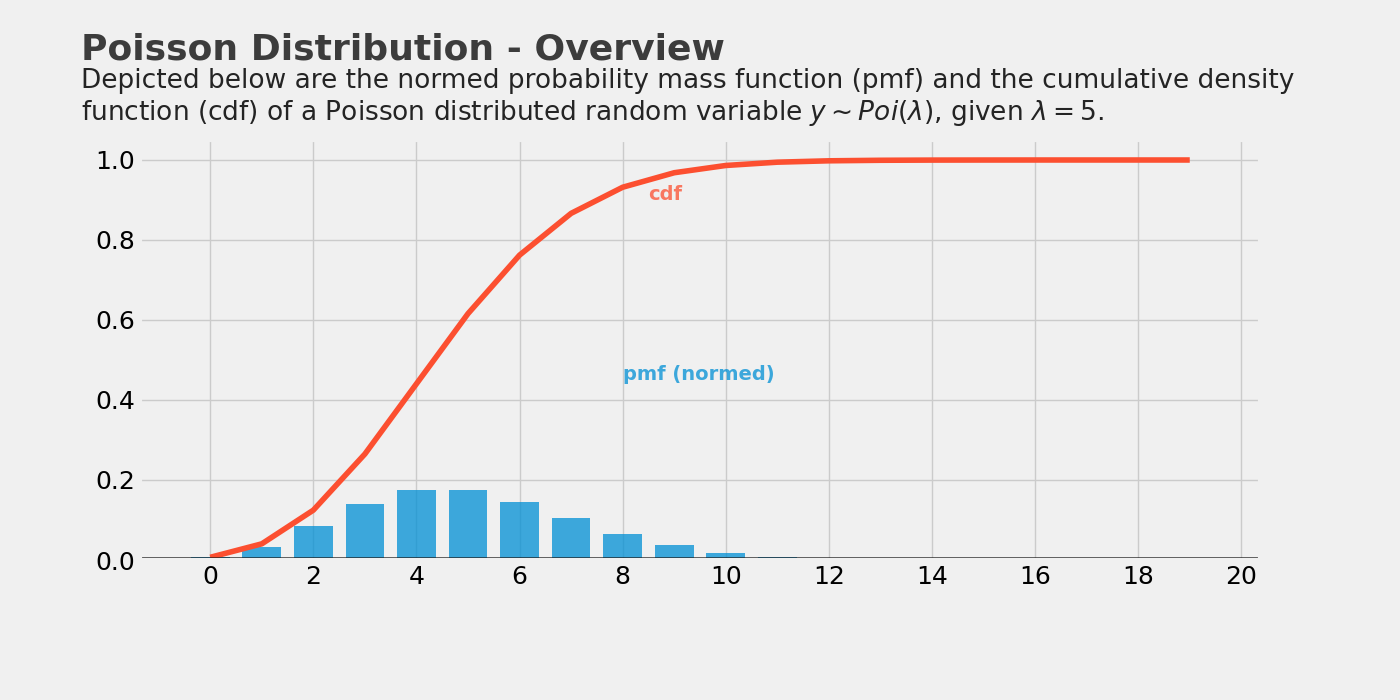
泊松分布图像绘制
# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
# PLOTTING CONFIG
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)
# PDF
plt.bar(x=np.arange(20),
height=(stats.poisson.pmf(np.arange(20), mu=5)),
width=.75,
alpha=0.75
)
# CDF
plt.plot(np.arange(20),
stats.poisson.cdf(np.arange(20), mu=5),
color="#fc4f30",
)
# LEGEND
plt.text(x=8, y=.45, s="pmf (normed)", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=8.5, y=.9, s="cdf", alpha=.75, weight="bold", color="#fc4f30")
# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis='both', which='major', labelsize=18)
plt.axhline(y=0.005, color='black', linewidth=1.3, alpha=.7)
# TITLE, SUBTITLE & FOOTER
plt.text(x=-2.5, y=1.25, s="Poisson Distribution - Overview",
fontsize=26, weight='bold', alpha=.75)
plt.text(x=-2.5, y=1.1,
s='Depicted below are the normed probability mass function (pmf) and the cumulative density\nfunction (cdf) of a Poisson distributed random variable $ y \sim Poi(\lambda) $, given $ \lambda = 5 $.',
fontsize=19, alpha=.85)
# 调整空白
plt.subplots_adjust(left=0.1, bottom=0.2, right=0.9, top=0.8, wspace=0.5, hspace=0.5)
plt.show()
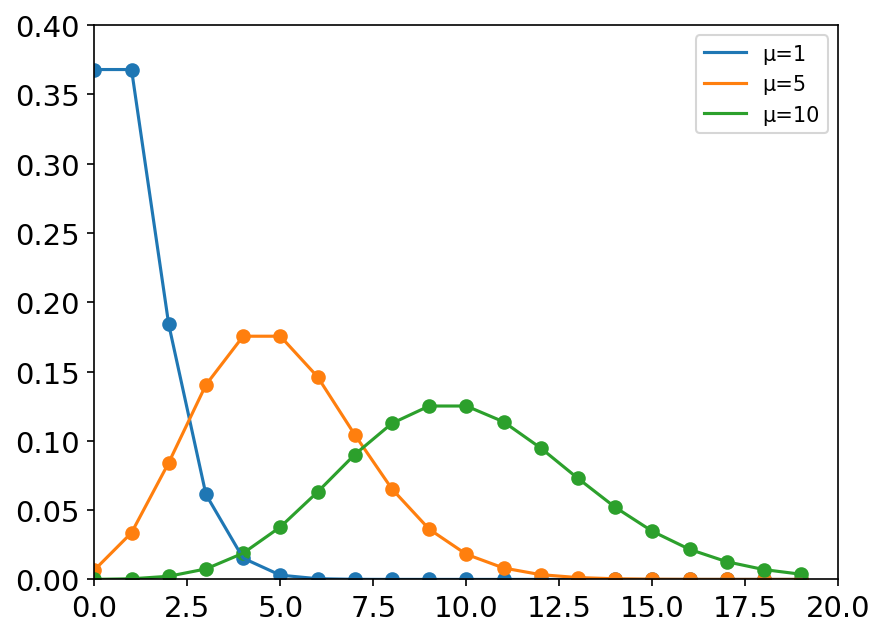
x = np.arange(20)
mu_list = [1, 5, 10]
plt.figure(dpi=150)
for mu in mu_list:
y = stats.poisson.pmf(x, mu=mu)
plt.axis([0, 20, 0, 0.4])
plt.tick_params(axis='both', labelsize=14)
plt.scatter(x, y)
plt.plot(x, y,label='μ={}'.format(mu))
plt.legend(loc='best')
plt.show()
参考连接