一、简介与使用场景
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。这是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用
贪心算法
的策略,
每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
Dijkstra算法的使用场景:
一定要是单源最短路径且每条边的权重必须是正值
单源最短路径:希望找到从(一个)源节点到每个结点的最短路径;
二、算法思想
Dijkstra算法主要是基于贪心的策略,
始终保持当前迭代解为当前最优解
。意思就是在已知的条件下或是当前拥有的全部条件下保证最优解,若在此后的迭代中由于加入了新的条件使得
产生了更优解则替代此前的最优解
。通过不断的迭代不断保证每次迭代的结果都是当前最优解,当迭代到
最后一轮时得到的就会是全局最优解。
步骤:
比如说现在要求1到n节点的最短距离。
我们可以用一个bool数组
st
记录每个边
是否已经被确定为最短路。
再用一个
dist
数组记录每个节点到源点的距离。
1️⃣ 先把第一个节点的距离记为0(
dist[1] = 0
),其他的节点距离记为正无穷。
2️⃣ 循环n – 1次,每一次循环内部再遍历所有节点,找到(不在
st
数组内的)最小权值的节点。再把这个节点加入到
st
中。
3️⃣ 用找到的这个节点更新其他(与他相连)节点的
dist
。
第一次找到x节点的时候一定从源点到x节点的最短路径。
举个例子:

先把①的dist变成0,其他的dist为正无穷。
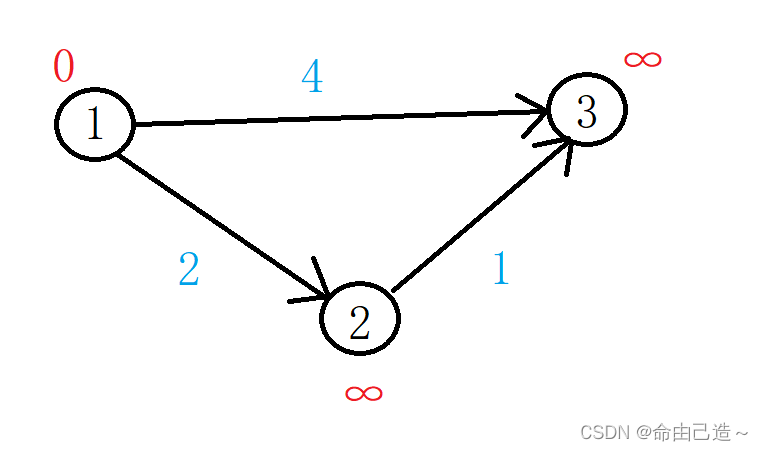
循环两次,第一次找到了①节点。然后利用①更新没有确定已经是最短路径的节点,也就是2和3。而此时①就已经确定了他自己的最短路径,标记
st
为true。
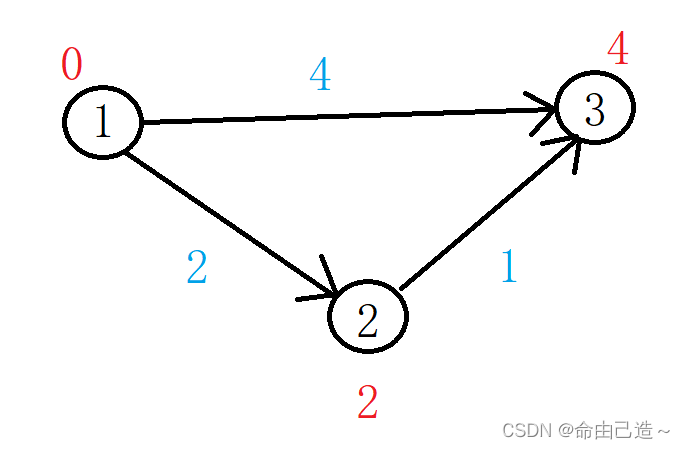
第二次循环找到了②节点,那么利用②来处理还没有确定的节点,只剩下③。
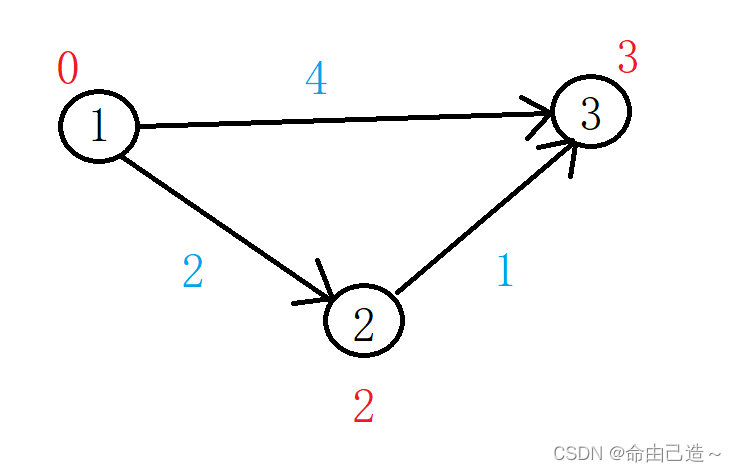
由此单源最短路径就已经找到。
三、朴素版Dijkstra
用一道例题来讲解:
题目链接
题目描述:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500,1≤m≤105,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路分析:
因为这道题的给的是稠密图,所以用
邻接矩阵
来存储。
而存在重边所以初始化邻接矩阵的时候每次要判断是不是最小,取最小值即可。
而如果存在自环,只需要最后判断n节点有没有被处理即可。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
int n, m;
int g[N][N];// 邻接矩阵
int dist[N];// 距离
bool st[N];// 是否已经确定了最短路径
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;// 初始化第一个节点
for(int i = 0; i < n - 1; i++)// 循环n - 1次
{
int t = -1;// 找最小节点
for(int j = 1; j <= n; j++)
{
if(!st[j] && (t == -1 || dist[j] < dist[t]))
{
t = j;
}
}
if(t == n) break;// 找了n节点是最小说明n已经确定为最短路径了
st[t] = true;
// 更新其他节点
for(int j = 1; j <= n; j++)
{
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(g, 0x3f, sizeof g);
cin >> n >> m;
int a, b, c;
while(m--)
{
cin >> a >> b >> c;
g[a][b] = min(g[a][b], c);
}
cout << dijkstra() << endl;
return 0;
}
四、堆优化版Dijkstra
而如果题目给的是一个稀疏图,我们还用上面的算法(时间复杂度为O(N^2)),可能会超时。
所以有了一个优化版本的Dijkstra算法。
通过分析朴素版本的代码,可以看到每次都要暴力遍历所有的边找到最小的距离,所以我们
可以使用堆,每次堆顶都是最小的边。
来看一道例题:
题目链接
题目描述:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×105,图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 109。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路描述:
大致思路跟朴素版一样,而我们怎么用优先级队列来得到最小距离的节点呢?
我们可以用
pair<int, int>
来存储,
first
代表距离,
second
代表节点。
这里用数组模拟邻接表在上一章有讲解:
【数据结构与算法】图——邻接表与邻接矩阵
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 150010;
int n, m;
int h[N], e[N], ne[N], w[N], idx;
bool st[N];
int dist[N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
priority_queue<PII, vector<PII>, greater<PII>> pq;
pq.push({0, 1});
dist[1] = 0;
while(pq.size())
{
auto t = pq.top();
pq.pop();
int node = t.second, val = t.first;
if(st[node]) continue;
st[node] = true;
// 更新其他节点
for(int i = h[node]; i != -1; i = ne[i])
{
int j = e[i];
dist[j] = min(dist[j], w[i] + dist[node]);
pq.push({dist[j], j});
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
int a, b, c;
while(m--)
{
cin >> a >> b >> c;
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
五、总结
Dijkstra算法用来解决的是单源最短路径且没有负权值的问题。
并不是所有的题目都用优化版本的,而是稠密图用朴素版Dijkstra,稀疏图用堆优化版Dijkstra。