数字滤波器的作用是滤除不感兴趣的信号,留下想要的信号。数字滤波器可分为无限脉冲响应(IIR)数字滤波器、有限脉冲响应(FIR)数字滤波器两种,两者各有优缺点,其中FIR数字滤波器因其具有良好的线性相位特性受到广泛应用,线性相位是指信号中各频率成分的相对相位关系不改变,即信号经过具有线性相位特性的滤波器后各个频率分量的延迟时间是一样的,IIR数字滤波器在达到相同性能指标时所需的阶数更小,所需成本更低,但相位非线性,因此在选择滤波器时需要多方面考虑,在对相位要求不敏感的场合,如语音通信等,选用IIR较为合适,这样可以充分发挥其经济高效的特点;在对线性相位要求较高的场合,如雷达、图像处理、数据传输等以波形携带信息的系统则需使用FIR数字滤波器。
MATLAB中有很多方法可以实现FIR数字滤波,例如使用fir1函数先得到滤波器系数h,然后使用filter/conv函数将所得系数h与滤波器输入信号进行卷积。本文主要介绍一种更灵活直观的图形化滤波器设计方法,即利用MATLAB自带的Filter Designer工具箱,通过设置相关参数完成FIR数字滤波器的设计,还可以将滤波器系数生成coe文件用于FPGA实现。其打开方法为:在MATLAB工具栏中找到”“APP”,从下拉栏里选中Filter Designer即可,如下图所示。

然后设置相关参数:
Response Type:选择滤波器的类型:低通、高通、带通和带阻等。
Design Method:FIR滤波器设计方法有多种,最常用的是窗函数设计法(Window)、等波纹设计法(Equiripple)和最小二乘法(Least-Squares)等。其中窗函数设计法在学校课堂中是重点讲解的,提到FIR滤波器肯定会想到hamming、kaiser窗,但是实际应用中却很少使用,因为如果采用窗函数设计法,达到所期望的频率响应,与其它方法相比往往阶数会更多;而且窗函数设计法一般只参照通频带wp、抑制频带ws和理想增益来设计滤波器,但是实际应用中通频带和抑制带的波纹也是需要考虑的,那在这种情况下,采用等波纹设计法就非常适用了。
Filter Order:设置滤波器的阶数,这个选项直接影响滤波器的性能,阶数越高,性能越好,但是相应在FPGA实现耗用的资源更多。在这个设置中提供2个选项:Specify order和Minimum order,Specify order是用户自己确定滤波器的阶数,其值等于滤波器阶数-1,Minimum order是让工具自动确定达到期望的频率相应所需要的最小阶数。
Frequency Specification:设置频率响应的参数,包括采样频率Fs、通带频率Fpass和阻带频率Fstop,通带频率可以理解为让小于Fpass的频率通过,阻带频率可以理解为让大于Fstop的频率被抑制。
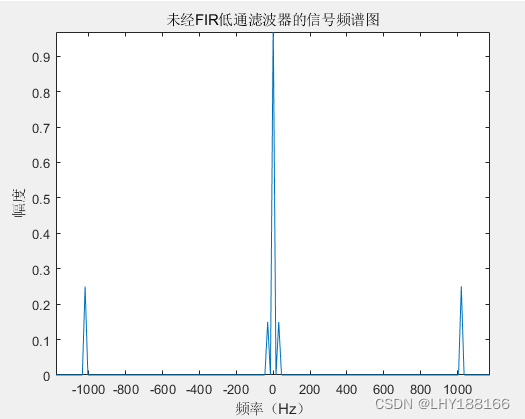
本文以设计一个FIR低通滤波器来将包含有直流、30Hz、1020Hz三种频率成分的信号(频谱图如下图所示)中的1020Hz高频成分滤除为例,介绍滤波器参数设置方法。(画频谱图的方法见上一篇文章——信号处理之FFT)。
参数设置如下图所示。
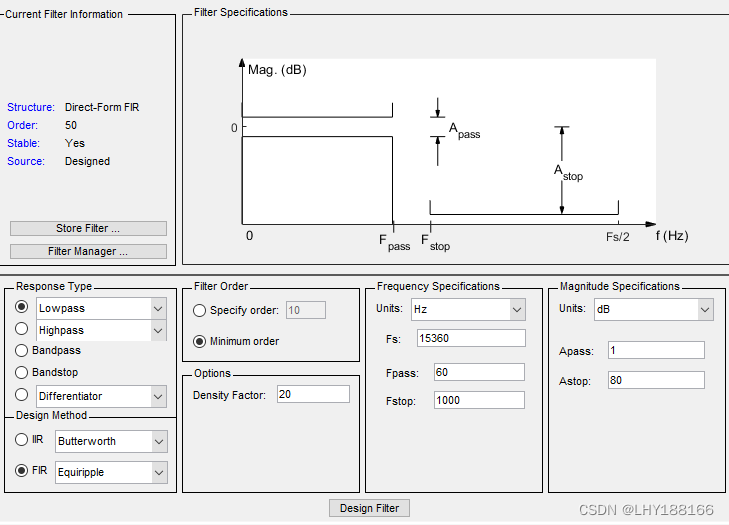
Response Type选择低通,Design Method选择FIR等波纹设计法,Filter Order选择Minimum order,Frequency Specification中采样率设置为15360Hz,为了尽量不衰减30Hz低频分量,通带频率设置为60Hz,为了对1020Hz高频分量起到较好的衰减效果,阻带频率设置为1000Hz。
参数设置完成后,点击“Design Filter”,即可看到所设计的滤波器阶数为41阶以及滤波器的幅频响应曲线,可观察对不同频率成分的衰减情况,如下图所示。
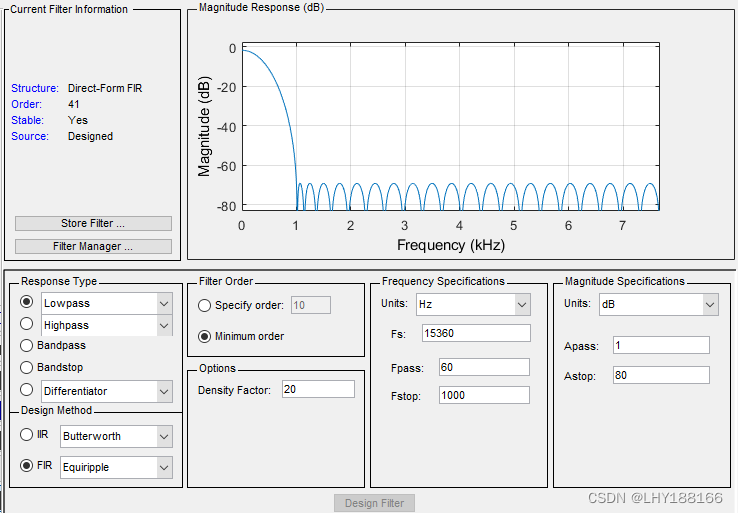
从上图的幅频响应曲线可以看出在1020Hz处有约60dB的衰减,根据-60=20lg(衰减前幅值/衰减后幅值)可知,衰减后的幅值是衰减前的千分之一,即可以较好地滤除1020Hz的频率成分。通过按照下图所示步骤即可生成Matlab代码。

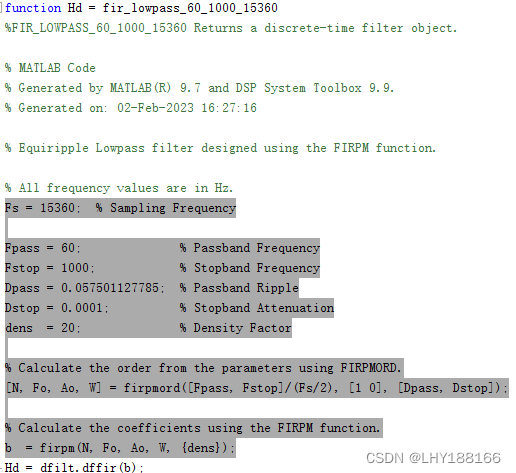
生成代码后有两种方式进行滤波,方法一:直接使用filter(fir_lowpass_60_1000_15360,e);其中fir_lowpass_60_1000_15360为生成的函数名,e为滤波器的输入信号。
方法二:将所生成的代码中的阴影部分复制粘贴到主程序,再使用conv(e,b,’same’)。
经过FIR低通滤波器后的信号,其频谱图如下图所示。
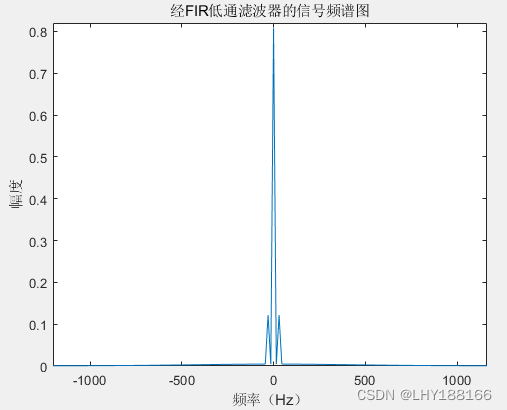
从图中可以看出1020Hz的高频成分被滤波,只剩下直流分量和30Hz低频分量。
完整代码如下:
%% FIR滤波器 by CSDN LHY188166
clc;
clear;
close all;
fs_mf = 15360; %采样率
N = 1024; %采样点数/FFT点数
ma = 0.3; %30Hz信号调制深度
mb = 0.5; %1020Hz信号调制深度
mf = 0.3; %9960Hz调频副载波对载波的调制深度,调制度30%±2%
F_30 = 30; %30Hz频率分量
F_1020 = 1020; %1020Hz频率分量
t = 0:1/fs_mf:(N-1)/fs_mf;
%% 合成信号 1为直流分量
e =1+ma.*sin(2*pi*F_30.*t)+0.5*sin(2*pi*F_1020.*t);
%% 画信号频谱图
[x11,freq] = fft_plot(e,fs_mf);
figure;
plot(freq,abs(x11));
xlabel('频率(Hz)');
ylabel('幅度');
title('未经FIR低通滤波器的信号频谱图');
% Fs = 15360; % Sampling Frequency
%
% Fpass = 60; % Passband Frequency
% Fstop = 1000; % Stopband Frequency
% Dpass = 0.057501127785; % Passband Ripple
% Dstop = 0.0001; % Stopband Attenuation
% dens = 20; % Density Factor
%
% % Calculate the order from the parameters using FIRPMORD.
% [N, Fo, Ao, W] = firpmord([Fpass, Fstop]/(Fs/2), [1 0], [Dpass, Dstop]);
%
% % Calculate the coefficients using the FIRPM function.
% b = firpm(N, Fo, Ao, W, {dens});
% fir_600_1 =conv(e,b,'same');
fir_600 = filter(fir_lowpass_60_1000_15360,e);
%% 画经过600Hz低通滤波器后的频谱图
[x12,freq2] = fft_plot(fir_600,fs_mf);
figure;
plot(freq2,abs(x12));
xlabel('频率(Hz)');
ylabel('幅度');
title('经FIR低通滤波器的信号频谱图');function Hd = fir_lowpass_60_1000_15360
%FIR_LOWPASS_60_1000_15360 Returns a discrete-time filter object.
% MATLAB Code
% Generated by MATLAB(R) 9.7 and DSP System Toolbox 9.9.
% Generated on: 02-Feb-2023 16:27:16
% Equiripple Lowpass filter designed using the FIRPM function.
% All frequency values are in Hz.
Fs = 15360; % Sampling Frequency
Fpass = 60; % Passband Frequency
Fstop = 1000; % Stopband Frequency
Dpass = 0.057501127785; % Passband Ripple
Dstop = 0.0001; % Stopband Attenuation
dens = 20; % Density Factor
% Calculate the order from the parameters using FIRPMORD.
[N, Fo, Ao, W] = firpmord([Fpass, Fstop]/(Fs/2), [1 0], [Dpass, Dstop]);
% Calculate the coefficients using the FIRPM function.
b = firpm(N, Fo, Ao, W, {dens});
Hd = dfilt.dffir(b);
% [EOF]
function [x,freq] = fft_plot(x,Fs)
%计算信号的双边幅度频谱和其横坐标、并调整使得横坐标中心频率为0Hz,输入:x为输入信号,Fs为采样频率,输出:x为输入信号的幅度频谱,freq为输入信号幅度频谱的横坐标
N = length(x);
%%计算频谱的横坐标,使得中心频率为0Hz
if mod(N,2)==0
k = -N/2:N/2-1;
else
k = -(N-1)/2:(N-1)/2;
end
T = N/Fs;
freq = k/T;
x= fft(x)/N;%fft并归一化
x= fftshift(x);
参考文献:https://blog.csdn.net/weixin_28951059/article/details/112188261
参考文献:https://blog.csdn.net/s09094031/article/details/83755663