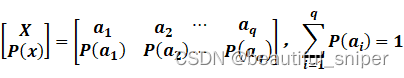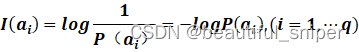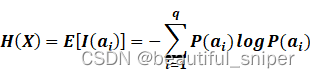博客

学院：

信息科学与工程学院

班级：

2020通信工程1班

姓名：

麦兜

实验名称

实验一、离散信源的熵

实验设备

（1）计算机    （2）所用软件：Matlab或C

实验目的

掌握信源的熵物理意义，概念；熟练掌握离散信源熵的计算方法步骤；利用Matlab编写离散信源熵的计算程序；验证程序的正确性。

实验内容

（1）根据熵计算的方法步骤，用Matlab编写离散信源熵的计算程序；

（2）用习题2.16和习题3.6(1)验证程序的正确性。

实




验




报




告




要




求

1. 简要总结信源的熵的物理意义，概念；
2. 写出离散信源熵计算的基本步骤，画出实现离散信源熵计算的程序流程图；
3. 实现离散信源熵计算的Matlab源程序；
4. 讨论信源的熵的大小与前后符号之间相关性的关系。

5、实验报告在实验后一周内交给老师，报告单一律用A4纸，以此单为封面，装订成册。

一、简要总结信源的熵的物理意义，概念

信源的熵的物理意义：指信源中的各个符号的平均不确定性;熵是信源符号的平均信息量，是信源符号的平均不确定度。

信源的熵的概念：信源发送一个符号所产生的信息量的平均值，我们把它称为熵。

二、写出离散信源熵计算的基本步骤，画出实现离散信源熵计算的程序流程图

设离散信源X，其概率空间为：

则其中事件ai的自信息为：

则信源的熵为：

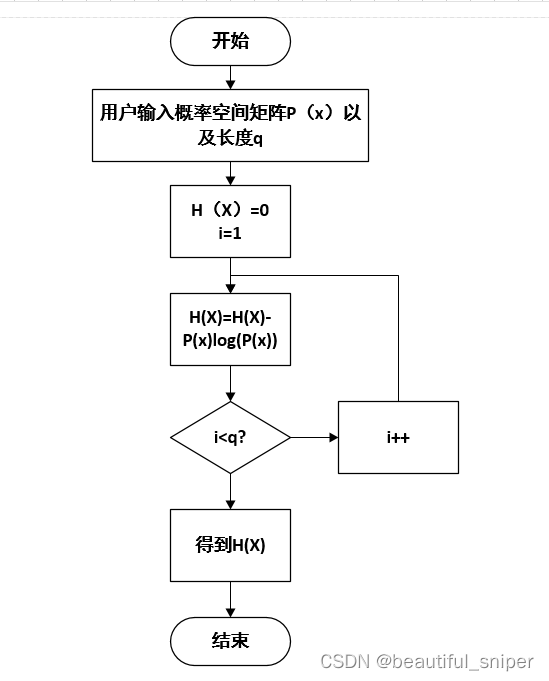
离散信源熵计算的程序流程框图如下：

三、实现离散信源熵计算的Matlab源程序

离散信源熵计算程序（exp1_H.m）

clc;

clear;

num=input(


‘


请输入事件的个数=’


);

p=input(


‘


请输入每一种事件的可能性=’


);

H=0;

for


i=1:num

H=H-p(i).*log2(p(i));

end

fprintf(


‘


该离散信源的熵为:%4f\n’


,H);

为验证习题2.16及3.6由离散信源熵计算程序改进成为条件熵计算程序（exp1_condition.m）

clc;

clear;

%H(X)

numx=input(


‘


请输入信源事件的个数=’


);

px=input(


‘


请输入每一种信源事件的可能性=’


);

Hx=0;

for


i=1:numx

Hx=Hx-px(i).*log2(px(i));

end

%H(XY)

pYX=input(


‘


请输入概率转移矩阵=’


);

px1=px’;

pxy=px1.*pYX;

s=size(pxy);

row=s(1);

line=s(2);

Hxy=0;

for


i=1:row

for


j=1:line

Hxy=Hxy-pxy(i,j).*log2(pxy(i,j));

end

end

%Hy

py=linspace(0,0,line);

Hy=0;

for


i=1:line

for


j=1:row

py(i)=py(i)+pxy(j,i);

end

end

for


i=1:line

Hy=Hy-py(i).*log2(py(i));

end

HXY=Hxy-Hy;

HYX=Hxy-Hx;

fprintf(


‘


该离散信源的熵H(X)=%4f\n’


,Hx);

fprintf(


‘H(X|Y)=%4f\n’


,HXY);

fprintf(


‘H(Y|X)=%4f\n’


,HYX);

四、讨论信源的熵的大小与前后符号之间相关性的关系。

信源的相关性是信源符号键的依赖程度的度量。由于信源输出符号间的依赖关系也就是信源的相关性使得信源的实际熵减小。信源输出符号间统计约束关系越长，信源的实际熵越小。当信源输出符号间彼此不存在依赖关系且为等概率分布时，信源的实际熵等于最大熵。