阵列信号学习笔记-重新整理
1-dimesion to 3-dimesion
Array- 阵列, 阵列中的传感器(mic)在阵列信号处理中被称为阵元,阵元一般排列在一条直线上, 也可以排列在二维或者三维体面上,阵元可以均匀排列, 也有不均匀排列的.
辐射波(反射)的源 被称为目标源,
近场源: 源离阵列较近, 波面为球面
远场源: 源离阵列较远, 波面近似平面
实际的阵列是处在三维空间的,以传感器为空间的原点,入射信号可以用俯仰角
φ
\varphi
φ
和方位角
θ
\theta
θ
来表示坐标方向,如下图所示。

波束形成理论
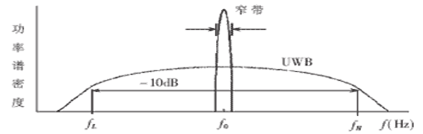
窄带和宽带
信号带宽远小于中心频率的是窄带信号,带宽能和中心频率相比拟或着是远大于中心频率的信号是宽带信号。
宽带信号与窄带信号是相对的,不满足窄带条件的信号就称为宽带信号。
窄带信号的功率集中在中心频率附近,两者的功率谱密度和频谱密度图有很大的差距。处理方法也有很大差距。
假设条件
均匀阵列,阵元的距离d是相等的。
研究的信号窄带远场信号,到达阵元的是一个平面波,载波能量可以集中在中心频率上。
信号和噪声之间互不相关,且认为是0均值的广义平稳随机过程,各阵元噪声功率相同
基于以上假设,定义远场目标源到达传感器的信号为
s
(
t
)
s(t)
s
(
t
)
是一个以
ω
0
\omega_0
ω
0
为中心频率的理想信号:
s
(
t
)
=
P
c
o
s
[
ω
0
t
+
ϕ
(
t
)
+
θ
]
=
P
e
j
[
ω
0
t
+
ϕ
(
t
)
+
θ
]
]
s(t)=\sqrt{P}cos{[\omega_0t+\phi(t)+\theta]}=\sqrt{P}e^{j[\omega_0t+\phi(t)+\theta]]}
s
(
t
)
=
P
c
o
s
[
ω
0
t
+
ϕ
(
t
)
+
θ
]
=
P
e
j
[
ω
0
t
+
ϕ
(
t
)
+
θ
]
]
3-dimesion to 2-dimesion
鉴于复杂性和考虑,学习阶段和简单的阵列处理一般采用线性阵列信号模型, 线性阵元和入射信号的关系确立了信号到达不同阵元的延时, 以入射方向和阵列直线的法线为夹角
θ
\theta
θ
的信号到达时延定义如下:
τ
=
d
∗
s
i
n
(
θ
)
c
\tau = \frac{d*sin(\theta)}{c}
τ
=
c
d
∗
s
i
n
(
θ
)
上边的公式表达是最常用的方式,下文都默认为这种形式。图示的这种定义如下:

有定义与法线夹角的的, 也有定义与阵元排列直线的夹角为
θ
\theta
θ
, 根据不同的定义,以入射方向和阵列直线为夹角
θ
\theta
θ
的信号到达时延定义如下:
τ
=
d
∗
c
o
s
(
θ
)
c
\tau = \frac{d*cos(\theta)}{c}
τ
=
c
d
∗
c
o
s
(
θ
)

阵列信号模型
以离信号最近的阵元作为参考,相邻的阵元可以表示为:
s
(
t
−
τ
)
=
s
(
t
)
e
−
j
ω
0
τ
=
s
(
t
)
e
−
j
ω
0
d
s
i
n
θ
/
c
=
s
(
t
)
e
−
j
2
π
d
s
i
n
θ
/
λ
0
s(t-\tau)=s(t)e^{-j\omega_0\tau} = s(t)e^{-j\omega_0dsin\theta/c}=s(t)e^{-j2\pi dsin\theta/\lambda_0}
s
(
t
−
τ
)
=
s
(
t
)
e
−
j
ω
0
τ
=
s
(
t
)
e
−
j
ω
0
d
s
i
n
θ
/
c
=
s
(
t
)
e
−
j
2
π
d
s
i
n
θ
/
λ
0
而以最邻近目标源的传感器作为第
1
1
1
个阵元,那么第
i
i
i
个阵元相对于第一个阵元所接收到的信号可以表示为:
s
i
(
t
)
=
s
(
t
−
(
i
−
1
)
τ
)
=
s
(
t
)
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
/
λ
0
s_i(t)=s(t-(i-1)\tau)=s(t)e^{-j2\pi (i-1)dsin\theta/\lambda_0}
s
i
(
t
)
=
s
(
t
−
(
i
−
1
)
τ
)
=
s
(
t
)
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
/
λ
0
假设M个距离为d的阵元,
K
K
K
个来自不同方向的窄带远场信号,其中第
i
i
i
个阵元接收到的信号可以表示为:
x
i
(
t
)
=
∑
k
=
1
K
s
k
(
t
)
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
k
/
λ
k
+
n
i
(
t
)
,
i
=
1
,
2
,
.
.
.
,
M
x_i(t)=\sum_{k=1}^K s_k(t)e^{-j2\pi (i-1)dsin\theta_k/\lambda_k}+n_i(t), i=1,2,…,M
x
i
(
t
)
=
k
=
1
∑
K
s
k
(
t
)
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
k
/
λ
k
+
n
i
(
t
)
,
i
=
1
,
2
,
.
.
.
,
M
用阵列入射角向量和信号源向量点乘表达这个第
i
i
i
个阵元接收信号
x
i
(
t
)
=
[
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
2
/
λ
2
,
.
.
.
,
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
k
/
λ
k
]
.
[
s
(
1
)
s
(
2
)
⋮
s
(
k
)
]
\bf{x_i}(t) = [e^{-j2\pi (i-1)dsin\theta_1/\lambda_1},e^{-j2\pi (i-1)dsin\theta_2/\lambda_2},…,e^{-j2\pi (i-1)dsin\theta_k/\lambda_k}].\begin{bmatrix} s(1) \\ s(2)\\ \vdots \\s(k) \end{bmatrix}
x
i
(
t
)
=
[
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
2
/
λ
2
,
.
.
.
,
e
−
j
2
π
(
i
−
1
)
d
s
i
n
θ
k
/
λ
k
]
.
⎣
⎢
⎢
⎢
⎡
s
(
1
)
s
(
2
)
⋮
s
(
k
)
⎦
⎥
⎥
⎥
⎤
很显然第一个
i
=
1
i=1
i
=
1
的阵元入射信号就是k个远场信号的直接相加
x
1
(
t
)
=
[
s
(
1
)
+
s
(
2
)
+
.
.
.
s
(
k
)
]
\bf{x_1}(t) = [s(1)+s(2)+ … s(k)]
x
1
(
t
)
=
[
s
(
1
)
+
s
(
2
)
+
.
.
.
s
(
k
)
]
如果定义噪声矢量
n
(
t
)
=
[
n
1
(
t
)
,
n
2
(
t
)
,
.
.
.
n
M
(
t
)
]
T
\bf{n}(t)=[n_1(t),n_2(t),…n_M(t)]^T
n
(
t
)
=
[
n
1
(
t
)
,
n
2
(
t
)
,
.
.
.
n
M
(
t
)
]
T
阵列信号的矩阵表达
x
(
t
)
=
A
s
(
t
)
+
n
(
t
)
\bf{x}(t)= \bf{A} \bf{s}(t) + \bf{n}(t)
x
(
t
)
=
A
s
(
t
)
+
n
(
t
)
输出矢量:
x
(
t
)
=
[
x
1
(
t
)
,
x
2
(
t
)
,
.
.
.
x
M
(
t
)
]
T
\bf{x}(t)=[x_1(t),x_2(t),…x_M(t)]^T
x
(
t
)
=
[
x
1
(
t
)
,
x
2
(
t
)
,
.
.
.
x
M
(
t
)
]
T
信号源矢量:
s
(
t
)
=
[
s
1
(
t
)
,
s
2
(
t
)
,
.
.
.
s
M
(
t
)
]
T
\bf{s}(t)=[s_1(t),s_2(t),…s_M(t)]^T
s
(
t
)
=
[
s
1
(
t
)
,
s
2
(
t
)
,
.
.
.
s
M
(
t
)
]
T
阵列方向矩阵
A
=
[
1
,
1
,
⋯
1
e
−
j
2
π
(
1
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
1
)
d
s
i
n
θ
2
/
λ
2
,
⋯
e
−
j
2
π
(
1
)
d
s
i
n
θ
k
/
λ
k
e
−
j
2
π
(
2
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
2
)
d
s
i
n
θ
2
/
λ
2
,
⋯
e
−
j
2
π
(
2
)
d
s
i
n
θ
k
/
λ
k
⋮
⋱
⋮
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
2
/
λ
2
,
⋯
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
k
/
λ
k
]
\bf{A}=\begin{bmatrix} 1, 1, & \cdots & 1 \\ e^{-j2\pi (1)dsin\theta_1/\lambda_1},e^{-j2\pi (1)dsin\theta_2/\lambda_2},& \cdots &e^{-j2\pi (1)dsin\theta_k/\lambda_k}\\ e^{-j2\pi (2)dsin\theta_1/\lambda_1},e^{-j2\pi (2)dsin\theta_2/\lambda_2},& \cdots &e^{-j2\pi (2)dsin\theta_k/\lambda_k}\\ \vdots & \ddots & \vdots\\ e^{-j2\pi (M-1)dsin\theta_1/\lambda_1},e^{-j2\pi (M-1)dsin\theta_2/\lambda_2},& \cdots &e^{-j2\pi (M-1)dsin\theta_k/\lambda_k} \end{bmatrix}
A
=
⎣
⎢
⎢
⎢
⎢
⎢
⎡
1
,
1
,
e
−
j
2
π
(
1
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
1
)
d
s
i
n
θ
2
/
λ
2
,
e
−
j
2
π
(
2
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
2
)
d
s
i
n
θ
2
/
λ
2
,
⋮
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
1
/
λ
1
,
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
2
/
λ
2
,
⋯
⋯
⋯
⋱
⋯
1
e
−
j
2
π
(
1
)
d
s
i
n
θ
k
/
λ
k
e
−
j
2
π
(
2
)
d
s
i
n
θ
k
/
λ
k
⋮
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
k
/
λ
k
⎦
⎥
⎥
⎥
⎥
⎥
⎤
阵列方向矩阵
A
=
[
a
(
θ
1
)
,
a
(
θ
2
)
,
.
.
.
a
(
θ
K
)
]
\bf{A}=[\bf{a}(\theta_1),\bf{a}(\theta_2),…\bf{a}(\theta_K)]
A
=
[
a
(
θ
1
)
,
a
(
θ
2
)
,
.
.
.
a
(
θ
K
)
]
阵列方向向量:
a
(
θ
k
)
=
[
1
,
e
−
j
2
π
d
s
i
n
θ
k
/
λ
0
,
.
.
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
k
/
λ
0
]
T
\bf{a}(\theta_k)=[1,e^{-j2\pi dsin\theta_k/\lambda_0},..e^{-j2\pi (M-1)dsin\theta_k/\lambda_0}]^T
a
(
θ
k
)
=
[
1
,
e
−
j
2
π
d
s
i
n
θ
k
/
λ
0
,
.
.
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
k
/
λ
0
]
T
阵列方向图
回忆上节的公式,简化为只有一个入射信号
θ
\theta
θ
,这样表达公式如下
y
(
t
)
=
∑
m
=
1
M
w
m
∗
s
d
(
t
)
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
/
λ
+
n
m
(
t
)
,
m
=
1
,
2
,
.
.
.
,
M
y(t)=\sum_{m=1}^M w^*_ms_d(t)e^{-j2\pi (m-1)dsin\theta/\lambda}+n_m(t), m=1,2,…,M
y
(
t
)
=
m
=
1
∑
M
w
m
∗
s
d
(
t
)
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
/
λ
+
n
m
(
t
)
,
m
=
1
,
2
,
.
.
.
,
M
令
β
=
2
π
d
s
i
n
θ
λ
\beta=2\pi \frac{dsin\theta}{\lambda}
β
=
2
π
λ
d
s
i
n
θ
y
(
t
)
=
∑
m
=
1
M
w
m
∗
s
d
(
t
)
e
−
j
(
m
−
1
)
β
,
m
=
1
,
2
,
.
.
.
,
M
y(t)=\sum_{m=1}^M w^*_ms_d(t)e^{-j (m-1)\beta}, m=1,2,…,M
y
(
t
)
=
m
=
1
∑
M
w
m
∗
s
d
(
t
)
e
−
j
(
m
−
1
)
β
,
m
=
1
,
2
,
.
.
.
,
M
令
w
m
=
1
(
m
=
1
,
2
,
.
.
.
,
M
)
w_m=1 ( m=1,2,…,M)
w
m
=
1
(
m
=
1
,
2
,
.
.
.
,
M
)
y
(
t
)
=
M
s
d
(
t
)
e
−
j
(
M
−
1
2
β
)
s
i
n
(
M
β
2
)
M
s
i
n
(
β
2
)
,
m
=
1
,
2
,
.
.
.
,
M
y(t)=M s_d(t)e^{-j(\frac{M-1}{2}\beta)}\frac{sin(\frac{M\beta}{2})}{Msin(\frac{\beta}{2})}, m=1,2,…,M
y
(
t
)
=
M
s
d
(
t
)
e
−
j
(
2
M
−
1
β
)
M
s
i
n
(
2
β
)
s
i
n
(
2
M
β
)
,
m
=
1
,
2
,
.
.
.
,
M
G
(
θ
)
=
∣
s
i
n
(
M
β
2
)
M
s
i
n
(
β
2
)
∣
G(\theta)=|\frac{sin(\frac{M\beta}{2})}{Msin(\frac{\beta}{2})}|
G
(
θ
)
=
∣
M
s
i
n
(
2
β
)
s
i
n
(
2
M
β
)
∣
上面的公式为阵列方向图公式。通过Octave帮忙绘制如下两种坐标形式的方向图。


波束形成
简而言之,对空间阵元信号的加权处理称为 波束形成。
波束成形,源于自适应天线的一个概念。接收端的信号处理,可以通过对多天线阵元接收到的各路信号进行加权合成,形成所需的理想信号。从天线方向图视角来看,这样做相当于形成了规定指向上的波束增益。
最简单的波束形成-相控阵
工作原理是对按一定规律排列的基阵阵元的信号均加以适当的移相(或延时)以获得阵波束的偏转,在不同方位上同时进行相位(或延时)补偿,即可获得多波束。
公式推导如下:
w
m
=
e
−
j
β
d
(
m
−
1
)
,
β
d
=
2
π
d
s
i
n
θ
d
λ
0
w_m=e^{-j\beta_d(m-1)}, \beta_d=2\pi\frac{dsin\theta_d}{\lambda_0}
w
m
=
e
−
j
β
d
(
m
−
1
)
,
β
d
=
2
π
λ
0
d
s
i
n
θ
d
带入下列公式
y
(
t
)
=
∑
m
=
1
M
w
m
∗
s
d
(
t
)
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
+
n
m
(
t
)
,
m
=
1
,
2
,
.
.
.
,
M
y(t)=\sum_{m=1}^M w^*_ms_d(t)e^{-j2\pi (m-1)dsin\theta_k/\lambda_0}+n_m(t), m=1,2,…,M
y
(
t
)
=
m
=
1
∑
M
w
m
∗
s
d
(
t
)
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
+
n
m
(
t
)
,
m
=
1
,
2
,
.
.
.
,
M
得到
G
(
θ
)
=
∣
s
i
n
[
M
2
(
β
−
β
d
)
]
M
s
i
n
[
1
2
(
β
−
β
d
)
]
∣
G(\theta)=|\frac{sin[\frac{M}{2}(\beta-\beta_d)]}{Msin[\frac{1}{2}(\beta-\beta_d)]}|
G
(
θ
)
=
∣
M
s
i
n
[
2
1
(
β
−
β
d
)
]
s
i
n
[
2
M
(
β
−
β
d
)
]
∣
θ
d
=
3
0
o
时
\theta_d=30^o时
θ
d
=
3
0
o
时
:


研究一下
β
d
=
2
π
d
s
i
n
θ
d
λ
0
\beta_d=2\pi\frac{dsin\theta_d}{\lambda_0}
β
d
=
2
π
λ
0
d
s
i
n
θ
d
这个公式有两个变量,还有一个变量就是传感器的距离
d
d
d
,而
λ
\lambda
λ
作为入射载波的波长,在固定目标源的时候基本作为一个常量来理解,当
θ
d
=
3
0
o
,
d
=
λ
/
2
时
\theta_d=30^o,d=\lambda/2时
θ
d
=
3
0
o
,
d
=
λ
/
2
时
:


出现栅瓣,这是空间信号混叠的效果,在均匀线阵中,利用不同空间位置的传感器对同一时刻的信号进行分别接收,得到了空间采样,阵元间距d引入的时延,可以认为是时间采样间隔,那么联系到奈奎斯特采样定理,这个“采样频率”
f
s
=
1
/
τ
≥
2
f
0
f_s = 1/τ ≥ 2f_0
f
s
=
1
/
τ
≥
2
f
0
推的如下空间采样的限制:
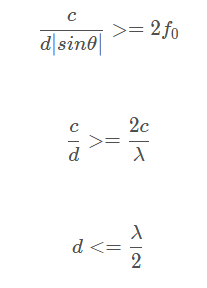
这里提出了空间阵列排布的一个限制,不要让mic的距离大于主要参考信号载波长度的一半。以声音信号为例:假设1000hz的单音信号源,因为声音在空气中的传播速度大约340米/秒,
λ
=
c
/
f
0
=
0.34
m
\lambda=c/f_0=0.34m
λ
=
c
/
f
0
=
0
.
3
4
m
。mic距离不能超过0.17m,典型声音信号截至频率为4k,mic距离最好不要超过0.04m,即4cm。
输入信噪比:
假设:信号来自,且与干扰和噪声不相关,噪声也是非相关噪声。
y
(
t
)
=
∑
m
=
1
M
w
m
∗
s
d
(
t
)
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
+
n
m
(
t
)
,
m
=
1
,
2
,
.
.
.
,
M
y(t)=\sum_{m=1}^M w^*_ms_d(t)e^{-j2\pi (m-1)dsin\theta_k/\lambda_0}+n_m(t), m=1,2,…,M
y
(
t
)
=
m
=
1
∑
M
w
m
∗
s
d
(
t
)
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
+
n
m
(
t
)
,
m
=
1
,
2
,
.
.
.
,
M
输入信噪比:
S
N
R
i
n
p
u
t
=
E
∣
s
d
(
t
)
∣
2
E
∣
n
m
(
t
)
∣
2
=
P
σ
n
2
SNR_{input}=\frac{E{|s_d(t)|}^2}{E{|n_m(t)|}^2}=\frac{P}{\sigma_n^2}
S
N
R
i
n
p
u
t
=
E
∣
n
m
(
t
)
∣
2
E
∣
s
d
(
t
)
∣
2
=
σ
n
2
P
令:
w
m
=
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
w_m=e^{-j2\pi (m-1)dsin\theta_k/\lambda_0}
w
m
=
e
−
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
代入
y
(
t
)
=
M
s
d
(
t
)
+
∑
m
=
1
M
n
m
(
t
)
e
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
,
m
=
1
,
2
,
.
.
.
,
M
y(t)=M s_d(t)+\sum_{m=1}^M n_m(t)e^{j2\pi (m-1)dsin\theta_k/\lambda_0}, m=1,2,…,M
y
(
t
)
=
M
s
d
(
t
)
+
m
=
1
∑
M
n
m
(
t
)
e
j
2
π
(
m
−
1
)
d
s
i
n
θ
k
/
λ
0
,
m
=
1
,
2
,
.
.
.
,
M
求得输出信噪比:
S
N
R
o
u
t
p
u
t
=
M
E
∣
s
d
(
t
)
∣
2
E
∣
n
m
(
t
)
∣
2
=
M
P
σ
n
2
=
M
.
S
N
R
i
n
p
u
t
SNR_{output}=\frac{ME{|s_d(t)|}^2}{E{|n_m(t)|}^2}=\frac{MP}{\sigma_n^2}=M.SNR_{input}
S
N
R
o
u
t
p
u
t
=
E
∣
n
m
(
t
)
∣
2
M
E
∣
s
d
(
t
)
∣
2
=
σ
n
2
M
P
=
M
.
S
N
R
i
n
p
u
t
自适应波束形成
根据接收到的阵列数据来更新波束形成器系数,以获得不同情境下的最优解决方案。若环境是变化的,系数也要自适应变化,这就是自适应波束形成
运用波束形成技术,利用麦克风阵列估计指定方向上的混有噪声和干扰的期望信号。这些麦克风阵元位于不同的空间位置,对声波进行空间采样,然后对采样信号进行处理以衰减干扰信号并提取期望信号。这样就得到一个特定的阵列空间响应,其主瓣指向期望信号而对干扰进行陷波
维纳滤波器:由数学家维纳(Rorbert Wiener)提出的一种以最小平方(统计准则)为最优准则的线性滤波器。
自适应滤波器:维纳滤波器是利用统计参数,实际应用中可能无法得到,需要借助迭代实现,这样就成了一个新框架→自适应滤波器
窄带自适应波束形成
经典结构图:
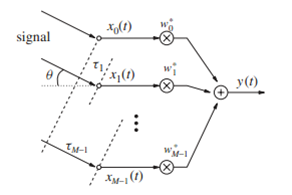
假设sd(t)是来自方向θd的期望信号,此外还有k个来自于不同方向的窄带远场干扰信号为i(t)
i
(
t
)
=
[
i
1
(
t
)
,
i
2
(
t
)
,
.
.
.
,
i
k
(
t
)
]
T
\bf{i}(t)=[i_1(t),i_2(t),…,i_k(t)]^T
i
(
t
)
=
[
i
1
(
t
)
,
i
2
(
t
)
,
.
.
.
,
i
k
(
t
)
]
T
定义A为干扰方向矩阵,噪声为n(t),进入阵列的矢量可以标识为:
x
(
t
)
=
a
(
θ
d
)
s
d
(
t
)
+
A
i
(
t
)
+
n
(
t
)
\bf{x}(t)=a(\theta_d)s_d(t)+Ai(t)+n(t)
x
(
t
)
=
a
(
θ
d
)
s
d
(
t
)
+
A
i
(
t
)
+
n
(
t
)
窄带波束形成就是寻找一组向量:
w
=
[
w
1
,
w
2
,
.
.
.
,
w
M
]
T
\bf{w}=[w_1,w_2,…,w_M]^T
w
=
[
w
1
,
w
2
,
.
.
.
,
w
M
]
T
在给定的信号和干扰环境中,依据某种最优准则,自适应的完成对期望信号的保留和干扰信号的滤除,这个过程被称为自适应波束形成,我们w称为权矢量。
宽带波束形成
在时域上可以理解为每一路都加一个横向滤波器:

实质上是一种可以对接收信号不同频率成分进行相位补偿的时域滤波器语音信号是典型的宽带信号。宽带处理的基础可以将信号DFT成子带,然后结合窄带的知识进行处理,最后IDFT回时域,得出所有滤波器的权值:

基于窄带的最小均方误差 MMSE
MMSE准则就是使估计的误差y(k)-dq(k)的军方值最小化,代价函数表述如下
J
(
w
q
)
=
E
[
∣
w
q
H
x
(
k
)
−
d
q
(
k
)
∣
2
]
\bf{J(w_q)}=E[|w_q^Hx(k)-d_q(k)|^2]
J
(
w
q
)
=
E
[
∣
w
q
H
x
(
k
)
−
d
q
(
k
)
∣
2
]
展开
J
(
w
q
)
\bf{J}(w_q)
J
(
w
q
)
如下
J
(
w
q
)
=
w
q
H
E
[
x
(
k
)
x
H
(
k
)
]
w
q
−
E
[
d
q
(
k
)
x
H
(
k
)
]
w
q
−
w
q
H
E
[
x
(
k
)
d
q
∗
(
k
)
]
+
E
[
d
q
(
k
)
d
q
∗
(
k
)
]
\bf{J(w_q)}=w_q^HE[x(k)x^H(k)]w_q-E[d_q(k)x^H(k)]w_q-w_q^HE[x(k)d_q^*(k)]+E[d_q(k)d_q^*(k)]
J
(
w
q
)
=
w
q
H
E
[
x
(
k
)
x
H
(
k
)
]
w
q
−
E
[
d
q
(
k
)
x
H
(
k
)
]
w
q
−
w
q
H
E
[
x
(
k
)
d
q
∗
(
k
)
]
+
E
[
d
q
(
k
)
d
q
∗
(
k
)
]
对上式求偏导:
d
d
w
q
J
(
w
q
)
=
2
E
[
x
(
k
)
x
H
(
k
)
]
w
q
−
2
E
[
x
(
k
)
d
q
∗
(
k
)
]
=
2
R
x
w
q
−
2
r
x
d
\frac{\bf d}{\rm{\bf{d}w_q}}J(w_q)=2E[x(k)x^H(k)]w_q-2E[x(k)d_q^*(k)]=2\bf{R_x}w_q-2\bf{r_{xd}}
d
w
q
d
J
(
w
q
)
=
2
E
[
x
(
k
)
x
H
(
k
)
]
w
q
−
2
E
[
x
(
k
)
d
q
∗
(
k
)
]
=
2
R
x
w
q
−
2
r
x
d
令
d
d
w
q
J
(
w
q
)
=
0
\frac{\bf d}{\rm{\bf{d}w_q}}J(w_q)=0
d
w
q
d
J
(
w
q
)
=
0
,可以得出最经典的维纳解,也是在MMSE意义下的最优权向量。
w
q
=
R
x
−
1
r
x
d
w_q=R_x^{-1}r_{xd}
w
q
=
R
x
−
1
r
x
d
LMS自适应算法
回顾前文的MMSE方法,考虑随机梯度算法,更新权向量的一般公式为:
w
q
(
k
+
1
)
=
w
q
(
k
)
−
1
2
μ
∇
w_q(k+1)=w_q(k)-\frac{1}{2}\mu\nabla
w
q
(
k
+
1
)
=
w
q
(
k
)
−
2
1
μ
∇
梯度算子用之前的偏导代换
∇
=
d
d
w
q
(
k
)
J
(
w
q
(
k
)
)
\nabla=\frac{\bf d}{\rm{\bf{d}w_q(k)}}J(w_q(k))
∇
=
d
w
q
(
k
)
d
J
(
w
q
(
k
)
)
,
μ
\mu
μ
为收敛因子,
∇
=
R
x
w
q
(
k
)
−
r
x
d
=
E
[
x
(
k
)
x
H
(
k
)
]
w
q
−
E
[
x
(
k
)
d
q
∗
(
k
)
]
\nabla=\bf{R_x}w_q(k)-\bf{r_{xd}}=E[x(k)x^H(k)]w_q-E[x(k)d_q^*(k)]
∇
=
R
x
w
q
(
k
)
−
r
x
d
=
E
[
x
(
k
)
x
H
(
k
)
]
w
q
−
E
[
x
(
k
)
d
q
∗
(
k
)
]
需要用瞬时值来代替数学期望,得出k时刻下面的梯度估计值:
∇
^
(
k
)
=
x
(
k
)
[
x
H
(
k
)
w
q
−
d
q
∗
(
k
)
]
=
x
(
k
)
f
(
k
)
\hat{\nabla}(k)=x(k)[x^H(k)w_q-d_q^*(k)]=x(k)f(k)
∇
^
(
k
)
=
x
(
k
)
[
x
H
(
k
)
w
q
−
d
q
∗
(
k
)
]
=
x
(
k
)
f
(
k
)
而
f
(
k
)
=
x
H
(
k
)
w
q
−
d
q
∗
(
k
)
f(k)=x^H(k)w_q-d_q^*(k)
f
(
k
)
=
x
H
(
k
)
w
q
−
d
q
∗
(
k
)
代表阵列输出与第
q
q
q
个期望相应
d
q
(
k
)
d_q(k)
d
q
(
k
)
的瞬时误差。有人证明,这个
∇
^
(
k
)
\hat{\nabla}(k)
∇
^
(
k
)
是真实梯度的无偏估计。这就是LMS自适应算法
w
q
(
k
+
1
)
=
w
q
(
k
)
−
μ
x
(
k
)
f
(
k
)
w_q(k+1)=w_q(k)-\mu x(k)f(k)
w
q
(
k
+
1
)
=
w
q
(
k
)
−
μ
x
(
k
)
f
(
k
)
经典的自适应波束形成
最小方差无畸变响应 MVDR-Minimum Variance Distortion-less Response
线性约束最小方差 LCMV- Linearly Constrained Minimum Variance
广义旁瓣消除器 GSC-Generalized Side-lobe Canceller
Frost波束形成
BF 实质是通过对阵元加权进行空域滤波,来达到增强信号、抑制干扰的目的
例如:MVDR是基于最大信干比准则的自适应波束形成算法,自适应的使矩阵输出在期望方向上功率最小,同时信干比最大。-
w
o
p
t
=
R
−
1
a
(
θ
d
)
a
H
(
θ
d
)
R
−
1
a
(
θ
d
)
\bf{w_{opt}}=\frac{R^{-1}a(\theta_d)}{a^H(\theta_d)R^{-1}a(\theta_d)}
w
o
p
t
=
a
H
(
θ
d
)
R
−
1
a
(
θ
d
)
R
−
1
a
(
θ
d
)
R
=
E
[
x
(
t
)
x
H
(
t
)
]
\bf{R}=E[x(t)x^H(t)]
R
=
E
[
x
(
t
)
x
H
(
t
)
]
该算法需要求矩阵的逆,以及要知道期望信号的波达方向
波达方向DOA
波束形成器有一个假设条件, 知道波源入射角,那么如何知道这个入射角就是波达方向研究的重点。空间测向DOA是通过对阵列接收信号进行统计处理以实现对空间信号的方向参数估计.
典型的测向方法:
波束形成测向方法
Capon最小功率估计器
ML极大似然估计器
MUSIC 多重信号分类方法
ESPRIT旋转不变量信号参数估计方法
波束形成测向方法
回忆阵列输出向量X(t),如果权矢量为
w
B
(
θ
)
=
1
M
[
1
,
e
−
j
2
π
d
s
i
n
θ
λ
0
,
.
.
,
e
−
j
2
π
(
M
−
1
)
d
s
i
n
θ
λ
0
]
T
\bf{w_B}(\theta)=\frac{1}{\sqrt{M}}[1, e^{-j\frac{2\pi d sin\theta}{\lambda_0}},.., e^{-j\frac{2\pi(M-1) d sin\theta}{\lambda_0}}]^T
w
B
(
θ
)
=
M
1
[
1
,
e
−
j
λ
0
2
π
d
s
i
n
θ
,
.
.
,
e
−
j
λ
0
2
π
(
M
−
1
)
d
s
i
n
θ
]
T
波束形成器的平均功率为
P
B
(
θ
)
=
w
B
H
(
θ
)
R
X
w
B
(
θ
)
P_B(\theta)=\bf{w}_B^H(\theta)R_Xw_B(\theta)
P
B
(
θ
)
=
w
B
H
(
θ
)
R
X
w
B
(
θ
)
在空间 对
θ
\theta
θ
进行扫描,得到空间谱图,那么极大值所对应的角度认为是信号的入射角DOA。
