BP神经网络的非线性曲线拟合和预测(未完)
曲线拟合常用到polyfit(多项式拟合函数)、lsqcurvefit(非线性拟合函数)、BP神经网络
其中lsqcurvefit需要特定的函数表达式而BP神经网络不要
曲线拟合有个好用的软件 1stopt
1.简单实例
根据已知工资数值来预测工资走向
P=[566 632 745 755 769 789 985 1110 1313
1428 1782 1920 2150 2292 2601 3149 4338
5145 5809 6241 6854 7656 8772 10007
11374 12567 14332 16614 19228 22844
26404 29688 32074];
%样本数据
%用于生成训练数据
重点内容
n=0;
for i=1:30
for j=(n+1):(n+3)
a(i,j-n)=P(j);% 566 632 745
% 632 745 755
% 745 755 769 a是用于训练的数据(样本集)
end
n=n+1;
end
t(1,:)=P(4:33);
%目标集
p=a’;
%样本集
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t);
%归一化函数
net=newff([-1 1;-1 1;-1 1],[5,1],{‘tansig’,’purelin’},’traingd’);
%初始化神经网络
net.trainParam.Lr=0.01;
%训练速度
net.trainParam.epochs=50000;
%训练时间
net.trainParam.goal=0.001;
%训练精度
net=train(net,pn,tn);
%训练函数 NET,P,T,[Pi],[Ai]
%利用原始数据对BP网络仿真
an=sim(net,pn);
%调用Simulink模型
a=postmnmx(an,mint,maxt);
%反归一化
%数据对比
x=1981:2010;
new=a;
%将训练完的数据赋给a
figure(2);
%画图窗口
plot(x,new,’r-o’,x,t,’b–+’);
%画图
legend(‘网络输出平均工资’,’实际输出平均工资’);
%对两条曲线的标识(通常在右上角)
xlabel(‘年份’);
ylabel(‘平均工资/元’);
title(‘数据对比图’);
%评价指标mse
%e=t-an
%perf=mse(e)
%预测,分五次预测,这是第一年的,以此类推就可以了
pnew=[26404 29688 32074]’;
[pnewn,minpnew,maxnew]=premnmx(pnew);
anewn=sim(net,pnewn);
anew=postmnmx(anewn,mint,maxt);
anew
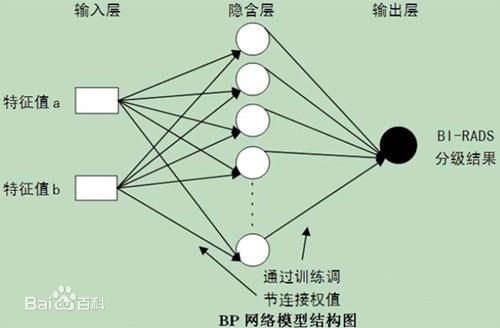
2.BP神经网络
1.流程
输入变量 输入目标值
归一化处理
创建神经网络
训练
调用sim
反归一化 -》输出拟合曲线
输入相应的值进行预测
2.特点与优点:
神经网络就是用向量乘法并广泛采用符号函数及各种逼近。并行、容错、可以硬件实现和自我学习特性。都是它的一般优点和特点。
3.BP(BackProgation)神经网络
按误差逆传播算法训练的多层前馈网络,能学习和存储大量的输入-输出模式映射关系。
4.传递函数
有两个,logsig(n)和tansig(n)
两个函数图像是否对应着 归一化【0,1】和归一化【-1,1】??
5.BP神经网络中
权值和阈值都是自动调整的不用预先设定。
6.newff函数
net=newff(PR,[S1,S2,…,Sn],{TF1,TF2,…,TFn},BTF,BLF,PF)
PR:输入向量的最小值和最大值
Si:第i层神经元个数
TFi:第i层传递函数
BTF:训练函数
BLF:权值/阈值学习函数
PF:性能函数
3.传入多参数来预测(有问题)
P=[
874 2 406;
900 2 398 ;
1165 3 480 ;
1087 2 404 ;
463 2 363 ;
815 3 447 ;
360 2 432 ;
277 2 504 ;
626 2 528 ;
645 2 520 ;
726 3 517 ;
394 3 437 ;
617 3 347 ;
524 3 505 ;
489 3 687 ;
577 3 495 ;
598 3 566 ;
475 2 466 ;
340 2 596 ;
421 2 547 ;
];
%样本数据
%用于生成训练数据
n=0;
for i=1:16
for j=(n+1):(n+4)
a(i,j-n)=P(j,1);
end
n=n+1;
end
t=P(5:20,1)’;
%目标集
,有转置!!
p=a(1:16,:)’;
%样本集,此处应该用a
,也有转置!!
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t);
%归一化函数
之前的转置和这里的归一化应该有点儿问题
net=newff([-1 1;-1 1;-1 1;-1 1],[5,1],{‘tansig’,’purelin’},’trainlm’);
%初始化神经网络
net.trainParam.Lr=0.01;
%训练速度
net.trainParam.epochs=500;
%训练时间
net.trainParam.goal=0.001;%训练精度
重点内容
net=train(net,pn,tn);
%训练函数 NET,P,T,[Pi],[Ai]
%利用原始数据对BP网络仿真
an=sim(net,pn);
%调用Simulink模型
a=postmnmx(an,mint,maxt);
%反归一化
%数据对比
x=1:16;
new=a;
%将训练完的数据赋给new
figure(2);
%画图窗口
plot(x,new,’r-o’,x,t,’b–+’);
%画图
legend(‘病毒感染预测输出’,’病毒感染实际输出’);
%对两条曲线的标识(通常在右上角)
xlabel(‘月份’);
ylabel(‘感染数(万)’);
title(‘病毒感染预测数据对比图’);
%评价指标mse
%e=t-an
%perf=mse(e)
%预测
% pnew=[22844 26404 29688]’;
% [pnewn,minpnew,maxnew]=premnmx(pnew);
% anewn=sim(net,pnewn);
% anew=postmnmx(anewn,mint,maxt);
% anew
%连续预测算法
pnew=[
598 3 566 ;
475 2 466 ;
340 2 596 ;
421 2 547 ;
];
%最后4个月病毒感染输出矩阵 不转置?
j=21;
tt=[360 550 466 414];
%真实数据用来检验误差
for i=1:4
%这里可以改预测次数1:n年
pnewn=tramnmx(pnew,minp,maxp);
%归一化
anewn=sim(net,pnewn);
%网络模型仿真
anew=postmnmx(anewn,mint,maxt);
%反归一化
fprintf(‘第%d月病毒感染预测值为:%g\n’,j,anew(:,1));
%预测值输出
number = abs((anew(:,1)-tt(i))/tt(i))*100;
%计算误差,获得误差的绝对值
number = strcat(num2str(number),’%’);
%转换为百分比
fprintf(‘第%d月误差为:%s\n’,j,number);
%误差输出
j=j+1;
%i=i+1;
%输入矩阵更新
pnew(1:3,1)=pnew(1:3,2);
pnew(1:3,2)=pnew(1:3,3);
pnew(1:3,3)=pnew(1:3,4);
pnew(1:3,4)=anew;
end
%真实数据
% 360 550 466 414
end
存在的问题:与一个输入参数比较,主要预测时出的结果有问题。会出现4个。
一个变量时,anew 1,anewn 1,pnew 4,pewne 4
三个变量时,anew 4,anewn 4,pnew 3×4,pewne 3×4