本篇文章内容如下:
1
)
m
序列的原理介绍
2
)
m
序列在
simulink
的产生
3
)
m
序列在
verilog
中的产生
正文:
一
m
序列的原理介绍
①伪随机信号(pn序列)是一种既有规律性,又有很好相关性的全频域信号形式。(其中相关性可以使用matlab中的xcorr函数进行计算。此处不展开说明)
②m序列(最长线性移位寄存器序列)是pn序列的特殊的一种,其特殊性在于:在反馈系数已知的情况下,m序列具有固定的周期(T=2n-1)和产生规律。m序列可由它的特征多项式直接计算产生出来。m序列的结果中,高电平数量仅仅比低电平数量多一个,(例如:10级m序列一个周期有1023个结果,其中高电平有512个,低电平有511个)即认为m序列的均值很小。
③pn序列产生原理:
如图1所示,n个移位寄存器和模二加法器(异或运算)形成闭环,每个加法器对应一个反馈系数,当反馈系数等于0的时候代表该寄存器不参与序列的产生。当反馈系数等于1的时候代表该寄存器参与序列的产生,为保证闭环首位反馈系数必须为零。
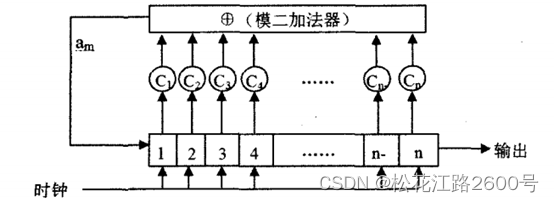
图1 pn序列原理图
可以使用特征多项式表示pn序列产生:
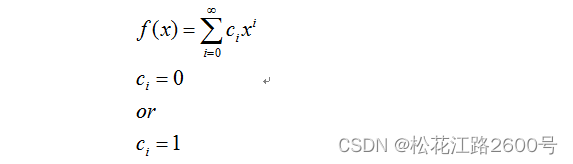
④当特征多项式满足以下条件的时候,其对应的多项式称之为本原多项式:
1)特征多项式法f(x)是不可约,即不能再分解出多项式
2)特征多项式法f(x)除不尽1+xp,其中p=1+n
3)特征多项式法f(x)能整除1+xq,其中q=2n-1
⑤每一个本原多项式对应一个m序列,本原多项式每一项系数对应每一个移位寄存器是否参与产生m序列,本原多项式的倒数(特殊长除法)的系数就是产生的m序列。
例如:4级m序列的多项式:f=x4+x+1。其倒数(注意:此处的长除法和常规长除法不同!):

图2
倒数q(x)=
x-4+ x-7+ x-8+ x-10+ x-12+ x-13+ x-14+ x-15
+x-19+…
对应m序列:100110101111000(15个码元,即周期为15)
⑥由于m序列的规律性,前人将每一级能够产生的m序列的情况进行汇总,使用时直接查阅即可(更高级数的m序列反馈系数可以自行百度),列表如下:
表1 m序列反馈系数汇总表

例如:以7级m序列反馈系数Ci=(211)8为例,首先将八进制的系数转化为二进制的系数即Ci=(010001001)2,由此我们可以得到各级反馈系数分别为:C0=1,C1=0,C2=0,C3=0,C4=1,C5=0,C6=0,C7=1,由此就很容易地构造出相应的m序列发生器。
二
m
序列在
simulink
的产生
通过PN sequence generator模块(simulink中固有的模块),改变其中多项式的系数就可以产生目标m序列。
例如:产生4级m序列的多项式:f=x4+x+1。将polynomial一项填写如图3所示。理论上对应m序列:100110101111000。下面对仿真结果(图4)进行对比。
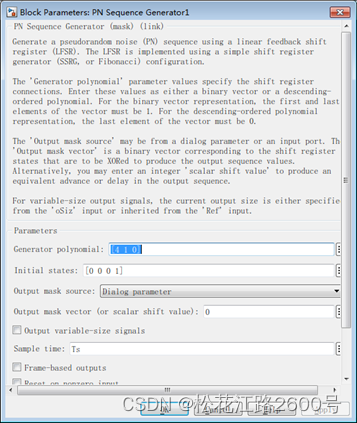
图3 仿真参数设置

图4 仿真结果
结论:实际产生的序列和理论序列完全一致。
三
m
序列在
verilog
中的产生
下面以10级m序列(一个周期产生1023个结果)的产生作为例子,在verilog中产生:
1)其中,m_seq是1023位结果,m_seq_long则是将m_seq增加头尾读取信号,便于在信号传输时候精准读取m序列结果。
2)通过改变代码中的poly和shift_reg的数量就可以实现不同级数m序列的产生。其中poly的选取和本原多项式一致。m序列的产生频率由使用者自定。
`timescale 1ns / 1ps
module m_seq_gen(
input clk,
input reset_n, //统一使用reset_n 作为复位键
output reg [1022:0] m_seq,
output reg [1087:0] m_seq_long ,//
output reg [9:0] shift_reg,
);
reg m_end ;
reg [31:0] n; //序列产生数量n
reg [9:0] POLY ; //
always@(posedge clk, negedge reset_n)//clk代表40MHZ ;
begin
if(!reset_n)
begin
shift_reg[9:0] <= 10'b11_1111_1111;
m_seq <= 1'b0;
POLY <= 10'b0000001001;
n <= 32'd0;
m_end <= 1'b1;
end
else
if(m_end == 1)
begin
m_seq_long <={32'b0000_0000_0000_0000_0000_0000_0000_0011,m_seq,1'b0,32'b0111_1111_1111_1111_1111_1111_1111_1111 };
shift_reg[9] <=
(shift_reg[0] & POLY[0])^
(shift_reg[1] & POLY[1])^
(shift_reg[2] & POLY[2])^
(shift_reg[3] & POLY[3])^
(shift_reg[4] & POLY[4])^
(shift_reg[5] & POLY[5])^
(shift_reg[6] & POLY[6])^
(shift_reg[7] & POLY[7])^
(shift_reg[8] & POLY[8])^
(shift_reg[9] & POLY[9]);//&按位与运算 等效于寄存器和反馈系数,^按位异或 等效于模二加法运算。
shift_reg[8:0] <= shift_reg[9:1] ;
if(n == 1022) //1022代表一个周期的结束,n代表序列的产生次数
begin
m_seq[n] <= shift_reg[0];
n <= 0;
m_end <= 1'b0;
end
else
begin
m_seq[n] <= shift_reg[0];
n <= n + 1'b1 ;
end
end
end
endmodule