课程目录索引
第一章 课程概述
.
第二章 控制设备
第2.2节 串行SPI接口控制PE4312数控衰减器
.
第三章 控制仪器
第3.2节 通过GPIB控制信号源
.
第3.3节 通过GPIB控制矢量网络分析仪
.
第3.4节 通过GPIB控制频谱仪
.
第四章 控制软件
第五章 综合案例一
第5.2节 应用工具包得到幅相加权
.
第5.3节 共用端口的SPI控制
.
第六章 综合案例二
第七章 综合案例三
第八章 课程总结
第5.2节 应用工具包得到幅相加权
5.2.1 Matlab的相控阵工具包
根据前一节的分析,为了能够最终完成对4×4共16组波控芯片(内部包含数控移相器和数控衰减器,SPI接口)的相位和衰减配置,首先要解决的问题就是如何得到所需配置的相位值矩阵和衰减值矩阵。
这个问题实际上可以转化成实现两个相互独立的函数:
-
移相值求解函数,输入工作频率f(单位Hz),波束指向俯仰角θ和方位角φ(单位deg),以及阵列单元间距dx与dy(单位mm)这三组量,得到相位值矩阵;
-
衰减值求解函数,输入窗函数类型和幅瓣抑制需求,得到衰减值矩阵。
注意在实际的工程应用中,这两个函数应该是通过C语言算法嵌入到组件内部的单片机、DSP中实现,但我们这里采用简陋但有效的解决方案,直接调用Matlab的工具包实现求解。
采用Matlab为R2019b(9.7.0.1190202)版本中的Sensor Array Analyzer 应用(Phased Array System Toolbox 4.2),为了更好通过方向图变化来观察现象,将以一个更大的16×16的阵列为例进行演示,选择基于全向天线 Isotropic的均匀矩形阵列URA(Uniform Rectangular Array),假定该阵列的工作频率为15GHz,为了满足±90°无栅瓣要求,单元间距dx=dy=10mm,由于扫描和加权过程相互独立,因此我们先不选择加权Taper选项,先观察波束扫描特性,设置如图1所示。
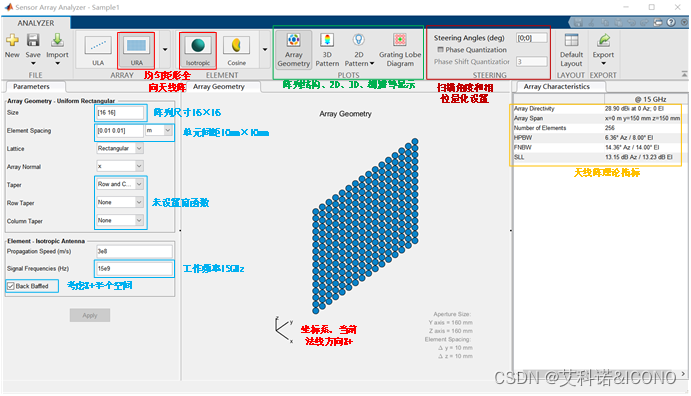
图 1 一个16×16的URA阵列实例
来观察相应的法向无扫描3D方向图和对应的二维UV方向图,如图2所示。
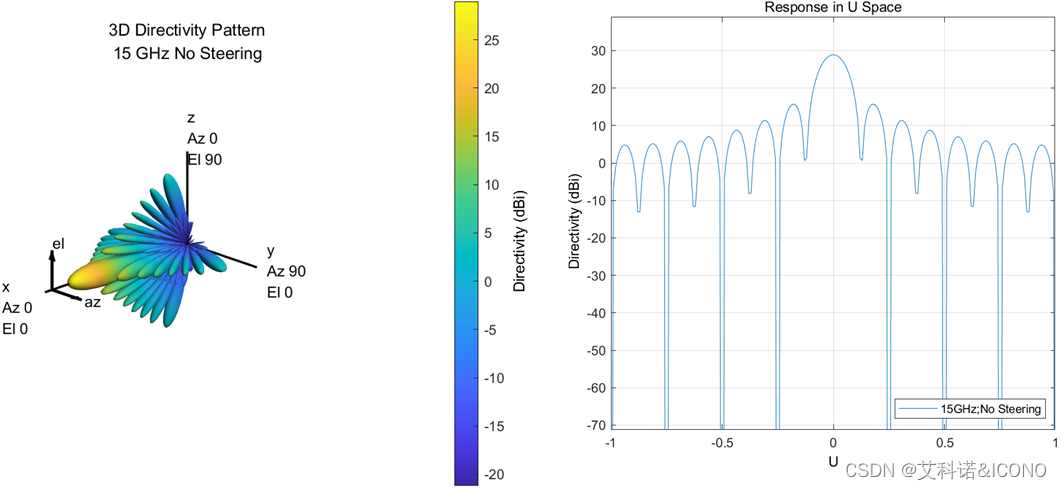
图 2 法向方向图(左)3D(右)UV
通过设置波束指向方位角(30°,0°)和俯仰角(0°,45°),可以观察相应方向图的变化。图3所示为方位角的扫描,可以观察到在坐标系Y轴和X轴平面进行扫描;图4所示为俯仰角的扫描,可以观察到在坐标系Z轴和X轴平面进行扫描。
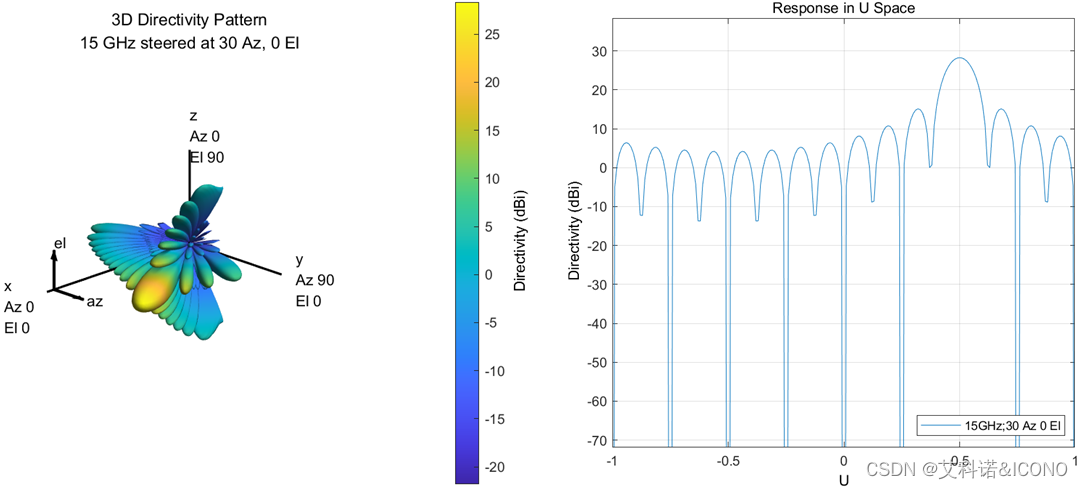
图 3 方位角扫描方向图
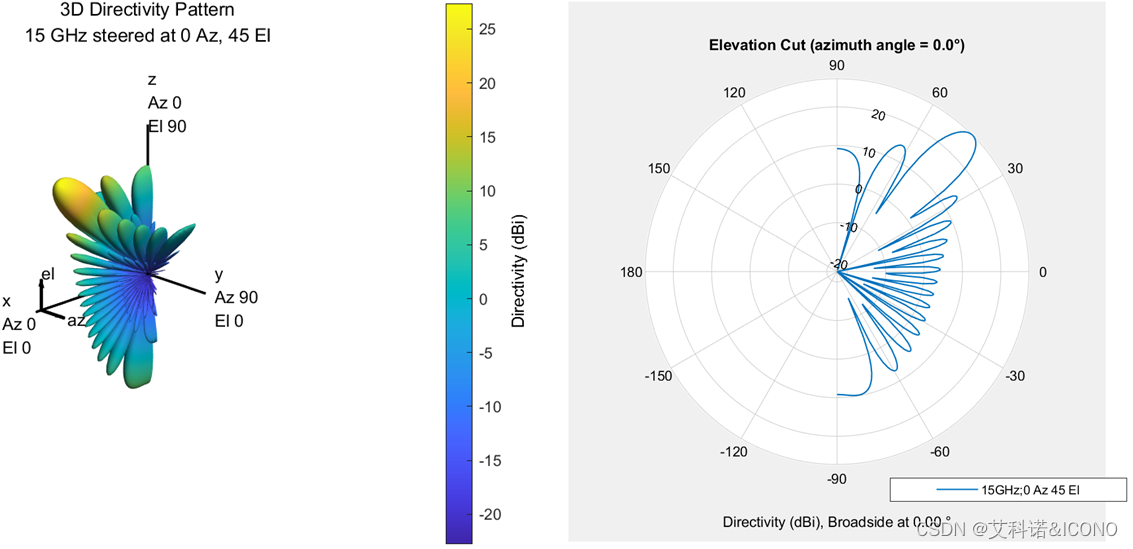
图 4 俯仰角扫描方向图
在观察了通过单元移相实现的波束空间扫描后,通过Taper来实现低幅瓣,在Row Taper和Column Taper的下拉菜单中,有Hamming、Chebyshev、Hann、Kaiser、Taylor和Custom选项(在写这部分的时候,其实我也并不太清楚它们的区别),选择Chebyshev并设置旁瓣衰减值为30dB(Sidelobe Attenuation),法向的三维方向图和二维方向图如图5所示。
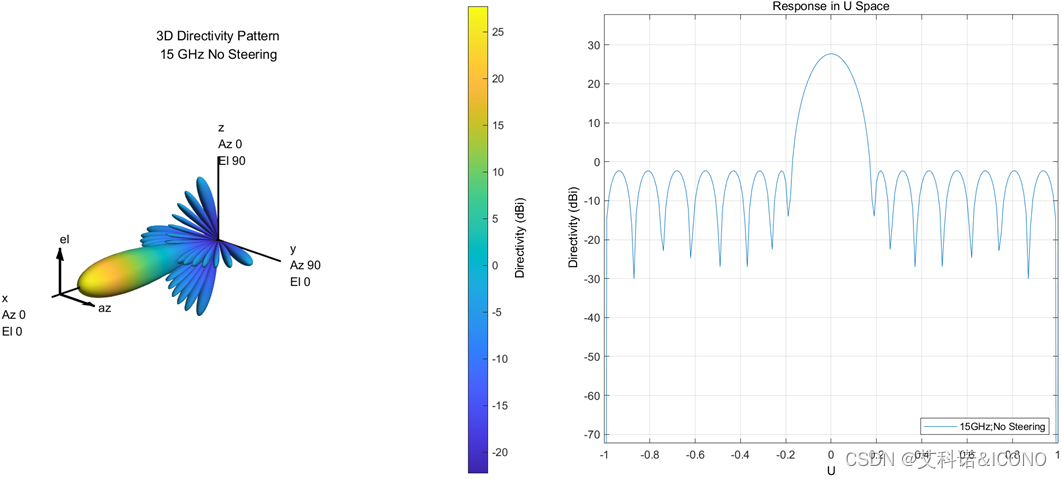
图 5 Taper后的法向方向图
此外注意观察右边阵列特性栏(Array Characteristics),Taper前后对比如图6所示。伴随着SLL也就是旁瓣抑制的提高,同时阵列方向性从28.9dBi降低到了27.72dBi,波束宽度也展宽了。这是实现低幅瓣的代价。

图 6 Taper前后的阵列指标对比(左)Taper前(右)Taper后
到这里,我们可以发现利用这个工具包,已经可以实现整个阵列天线的建模、扫描和加窗,但是要如何得到所需要的相位和衰减信息呢?接下来需要切换到界面后台的代码。
5.2.2 幅相转换为量化控制码
在图1界面的右上上角找到Export选项,下拉菜单中选择 Generate Matlab Script,就能够得到代码,我把它做了注释和重新组合,得到下面这个样子。
clear all; close all; clc;
%% 创建一个单元间距为10mm的16×16的URA阵列
Array = phased.URA('Size',[16 16],...
'Lattice','Rectangular','ArrayNormal','x');
Array.ElementSpacing = [0.01 0.01];
%% 该阵列的是由全向天线单元构成
Elem = phased.IsotropicAntennaElement;
Elem.BackBaffled = true;
Elem.FrequencyRange = [0 15000000000];
Array.Element = Elem;
%% 计算低幅瓣Taper
sll = 30;
rwind = chebwin(16, sll);
cwind = chebwin(16, sll);
taper = rwind*cwind.';
Array.Taper = taper.';
%% 计算扫描加权
SteeringAngles = [0;0]; % 设置波束扫描方向
Frequency = 15000000000; % 工作频率
PropagationSpeed = 300000000; % 光速
PhaseShiftBits = 0; % 相位量化
w = zeros(getNumElements(Array), length(Frequency));
SteerVector = phased.SteeringVector('SensorArray',Array, 'PropagationSpeed', PropagationSpeed, 'NumPhaseShifterBits', PhaseShiftBits(1));
for idx = 1:length(Frequency)
w(:, idx) = step(SteerVector, Frequency(idx), SteeringAngles(:, idx));
end
%% 绘制三维方向图1
Freq3D = Frequency;
format = 'polar';
Figure(1);
pattern(Array, Freq3D , 'PropagationSpeed', PropagationSpeed,...
'Type','directivity', 'CoordinateSystem', format,'weights', w(:,1));
前面为了引出这段代码,并帮助理解因此采用了工具包的界面来讲述,在后面的编程中不会用到这个工具包的界面,而将主要使用这段代码。
-
其中w变量,它以虚数的形式保存着每个天线单元的移相信息;
-
而Array.Taper中,则包含着幅度Taper的信息。
接下来要做的是将w与Array.Taper这两个16×16的矩阵转化成能够发给多功能芯片的数据格式。这里选用浙江铖昌科技有限公司的G4403模拟波束赋形芯片为例(我并没有实际使用过这款芯片,不过这类芯片的控制方法大同小异),其移相和衰减真值表如图7和图8所示。可以看到移相位数为6位,步进为5.625°。衰减位数也为6位,步进为0.5dB。
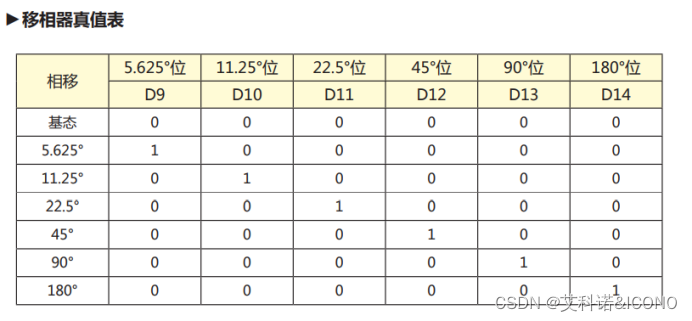
图 7 G4403移相器真值表
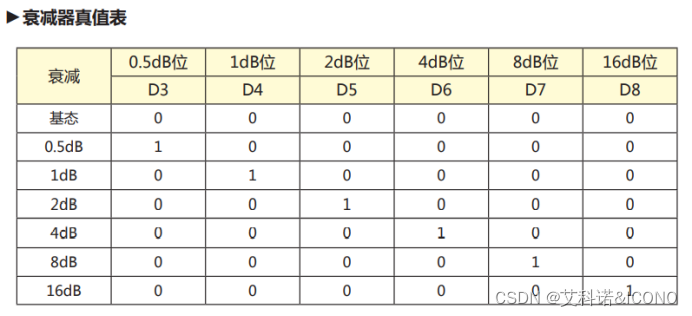
图8 G4403衰减器真值表
用下面的一段matlab代码整理w与Array.Taper的值。对于移相值,首先用matlab自带的phase函数提取w虚数的相位,后通过mod函数整理范围在0°~360°之间,最后除以最小量化步进5.625°。同样对于衰减值,首先由倍数值转化为分贝,后除以最小的衰减量化步进0.5dB。
%% 量化相位和幅度值
Phase_Shift = fix(mod(phase(w)*360/(2*pi),360)/5.625);
Att = fix(abs(10*log10(Array.Taper))/0.5);
注意我们这里得到的是10进制数,可以通过matlab中的dec2bin函数转化成2进制数进行检查。
5.2.3 量化控制码验证
为了验证转换的有效性,通过下面一段代码将量化后的相位和衰减值重新计算,绘制扫描3D方向图Figure2,拿Figure2与Figure1对比可以证明这种量化转换的正确性。
%% 量化相位和幅度值后的方向图2
Array.Taper = 10.^(-Att*0.5/10);
w_ = cos(Phase_Shift*5.625*2*pi/360)+sqrt(-1)*sin(Phase_Shift*5.625*2*pi/360);
figure(2);
pattern(Array, Freq3D , 'PropagationSpeed', PropagationSpeed,...
'Type','directivity', 'CoordinateSystem', format,'weights', w_(:,1));
如果我们增加移相器的最小步进到22.5°,增加衰减器的最小步进到2dB会发生什么,改动上述代码,绘制方向图3。
%% 增加相位步进和衰减步进后的方向图3
Phase_Shift = fix(mod(phase(w)*360/(2*pi),360)/22.5);
Att = fix(abs(10*log10(taper.'))/2);
Array.Taper = 10.^(-Att*2/10);
w_ = cos(Phase_Shift*22.5*2*pi/360)+sqrt(-1)*sin(Phase_Shift*22.5*2*pi/360);
figure(3);
pattern(Array, Freq3D , 'PropagationSpeed', PropagationSpeed,...
'Type','directivity', 'CoordinateSystem', format,'weights', w_(:,1));
前后三个3D方向图对比如图9所示。增加步进会恶化方向图,更进一步的实验可自行更改代码进行。
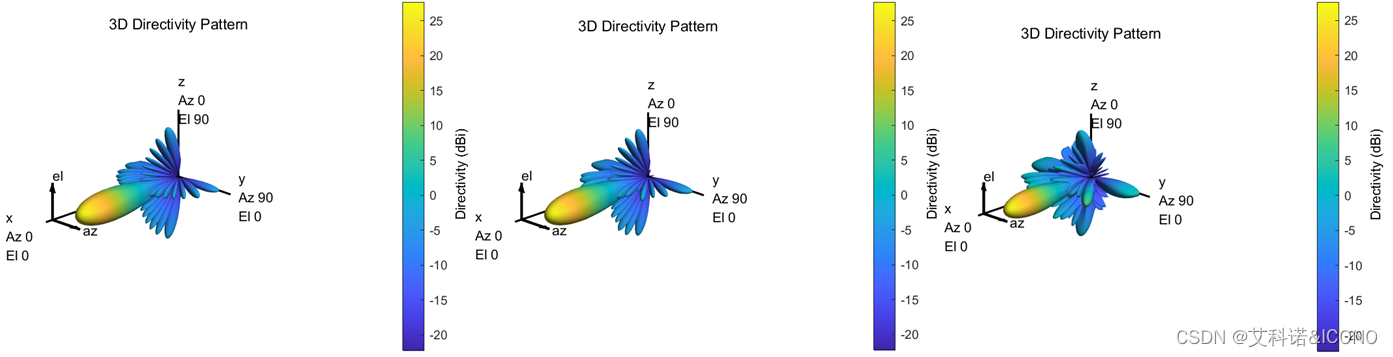
图9 (左)理想方向图;(中)6位量化方向图;(右)4位量化方向图
总结
到此,完成了我们本节的任务。简要回顾下,首先介绍了matlab中的相控阵工具箱,接下来通过建模导出后台代码,用后台代码得到我们所需要的相位和衰减值,并在量化后进行了验证。