[NOI2013]向量内积


图片摘自:https://www.cnblogs.com/Dragon-Light/p/6378185.html
3的情况写得不太对,只得了90,先贴着。


#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int maxn=1e5+10; int n,d,k,tot; int a[maxn][101],a3[maxn][101],b3[101][maxn],b[101][maxn],x[maxn],ans[maxn]; int tmp[101]; inline void find(int x) { int temp=0; for(int i=1;i<=n;i++) if(i!=x) { temp=0; for(int j=1;j<=d;j++) temp=(temp+a[i][j]*a[x][j])%k; if(temp==0) { if(i>x) swap(i,x); printf("%d %d",i,x); return; } } printf("-1 -1"); } int main() { scanf("%d%d%d",&n,&d,&k); for(int i=1;i<=n;i++) for(int j=1;j<=d;j++) scanf("%d",&a[i][j]),a[i][j]%=k; if(n<=1200) { for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) { long long tmp=0; for(int p=1;p<=d;p++) tmp=(tmp+(a[i][p]*a[j][p]))%k; if(tmp==0) { printf("%d %d",i,j); return 0; } } printf("-1 -1"); return 0; } else if(k==2) { for(int i=1;i<=n;i++) for(int j=1;j<=d;j++) b[j][i]=a[i][j]; int T=5; while(T--) { tot=0; memset(tmp,0,sizeof(tmp)); for(int j=1;j<=n;j++) x[j]=rand()%k,tot+=x[j]; tot%=k; for(int i=1;i<=d;i++) for(int j=1;j<=n;j++) tmp[i]=(tmp[i]+a[j][i]*x[j])%k; for(int i=1;i<=n;i++) { int temp=0; for(int j=1;j<=d;j++) temp=(temp+tmp[j]*b[j][i])%k; if(temp!=tot) { find(i); return 0; } } } printf("-1 -1"); } else { for(int i=1;i<=n;i++) for(int j=1;j<=d;j++) a3[i][j]=(a[i][j]*a[i][j])%k; for(int i=1;i<=n;i++) for(int j=1;j<=d;j++) b3[j][i]=a3[i][j]; int T=8; while(T--) { tot=0; memset(tmp,0,sizeof(tmp)); for(int j=1;j<=n;j++) x[j]=rand()%k,tot=(tot+x[j])%k; tot%=k; for(int i=1;i<=d;i++) for(int j=1;j<=n;j++) tmp[i]=(tmp[i]+a3[j][i]*x[j])%k; for(int i=1;i<=n;i++) { int temp=0; for(int j=1;j<=d;j++) temp=(temp+tmp[j]*b3[j][i])%k; if(temp!=tot) { find(i); return 0; } } } printf("-1 -1"); } return 0; }
View Code
[NOI2013]树的计数
B
F
S
在前的点的深度一定小于等于后面的点,所以
从Bfs序考虑比较容易,显然如果我们想好了如何给Bfs分层,就知道了答案。
分情况(只有序列相邻的两点才能判断是否分层):(记得要画图)
1、(必须不在同一层)对于bfs
连续
的ab两点,
假如a的bfs序小于b的bfs序,且a的dfs序大于b的
,那么他们之间肯定是要分层的,对答案贡献为1;
2、(必须在同一层)对于bfs
连续
的ab两点,
假如a的bfs序小于b的bfs序,且a的dfs序小于b的
,那么他们之间不能分层,贡献为0;
3、(在不在同一层都行)对于
dfs序
连续
的ab两点,
假如a的dfs序小于b的,且a的bfs序也小于b,
既可以与上一个点作为兄弟也可以作为儿子
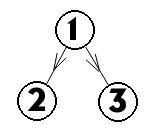
只能是2,3这样 ↑,贡献为0.5
4、第一个点要强制分层
CODE:


#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int maxn=2e5+10; int n,top; int Bfs[maxn],Dfs[maxn],nb[maxn],nd[maxn]; int fen[maxn],no[maxn],q[maxn]; double ans; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&Dfs[i]),nd[Dfs[i]]=i; for(int i=1;i<=n;i++) scanf("%d",&Bfs[i]),nb[Bfs[i]]=i; for(int i=1;i<n;i++) if(i==1 || nd[Bfs[i]]>nd[Bfs[i+1]]) fen[i]=1,no[i]=1; for(int i=1;i<=n;i++) fen[i]+=fen[i-1]; for(int i=1;i<n;i++) if(nb[Dfs[i]]<nb[Dfs[i+1]]) { if(fen[nb[Dfs[i]]-1]==fen[nb[Dfs[i+1]]-1]) q[++top]=nb[Dfs[i]]; else for(int j=nb[Dfs[i]];j<nb[Dfs[i+1]];j++) no[j]=1; } for(int i=1;i<=top;i++) if(no[q[i]]==0) ans+=0.5; ans+=fen[n]; printf("%.3lf",ans+1); return 0; }
View Code
转载于:https://www.cnblogs.com/linda-fcj/p/9141198.html