本次光线追踪系列从基础重新开始，主要参照

Ray Tracing in One Weekend

，具体实现代码框架见

https://github.com/RayTracing/raytracing.github.io/

。本文只是主要精炼光追相关理论，具体实现可参照原文。

电介质是水，玻璃和钻石等透明材料。当光线射到它们上时，它分裂为反射射线和折射（透射）射线。我们将通过在反射或折射之间随机选择，并且每次交互仅生成一条散射射线来解决这一问题。

本节将会实现折射向量和电介质材质的光线追踪，例如玻璃材质。

一、折射

对于折射，我们使用：



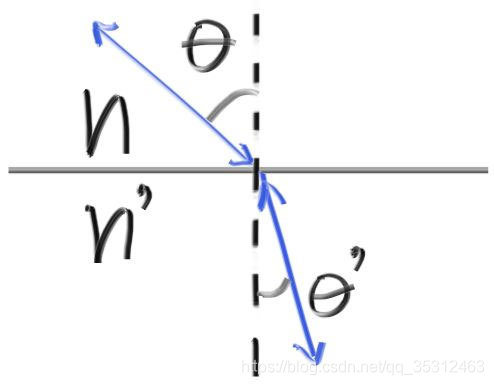
具体公式为：

其中，θ1,θ2 分别是入射角和折射角，η1,η2分别是两种介质的折射率。

已知入射光线向量I和法向量N，折射光线向量T的计算公式如下：



其中：



具体推导过程可参见原文。

写成代码如下：

bool refract(const vec3& v, const vec3& n, float ni_over_nt, vec3& refracted) {
    vec3 uv = unit_vector(v);
    float dt = dot(uv, n);
    float discriminant = 1.0 - ni_over_nt*ni_over_nt*(1-dt*dt);
    if (discriminant > 0) {
        refracted = ni_over_nt*(uv - n*dt) - n*sqrt(discriminant);
        return true;
    }
    else
        return false;
}

二、电介质材质

玻璃、水、钻石都是电介质，当光线通过它们内部，会发生折射（refraction），同时也会发生反射（reflection）。



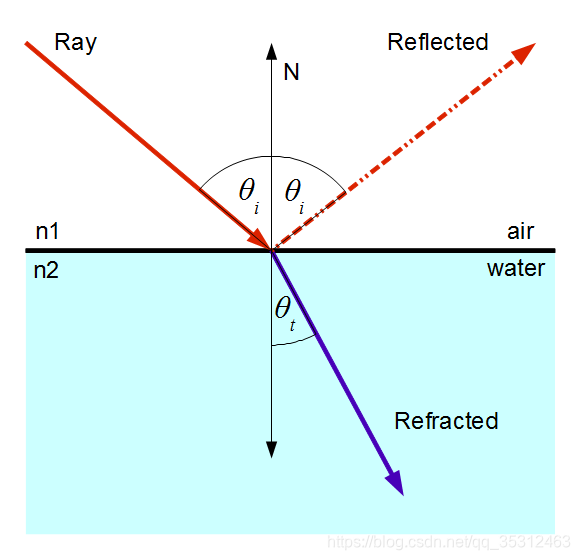
例如当我们远处看玻璃窗户的时候，基本就是透明的，但当我们贴着窗户看（视线和玻璃平面夹角很小）的时候，窗户能够像镜子一样反射一部分光。

如何计算反射和折射光强的比重呢？菲涅耳方程（Fresnel Formula）可以用来计算描述光在不同介质之间的反射比和透射比，但菲涅尔方程相当复杂，我们可以使用Fresnel-Schlick近似法求反射比的近似解(此处可参见之前PBR及之间的涅菲尔专题相关实现原理)：



代码实现如下：

float schlick(float cosine, float n1_over_n2) {
    float r0 = (1-n1_over_n2) / (1+n1_over_n2);
    r0 = r0*r0;
    return r0 + (1-r0)*pow((1 - cosine),5);
}

2.1 电介质类实现

如果是从里到外入射，即入射向量在法向量另外一侧的情况：

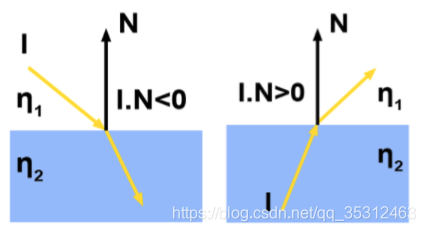
则要对法向量取反，并颠倒里外的折射率之比：

class dielectric : public material
{
public:
    dielectric(float ri) : ref_idx(ri) {} //n2/n1
    virtual bool scatter(const ray &r_in, const hit_record &rec, vec3 &attenuation, ray &scattered) const
    {
        vec3 outward_normal;
        vec3 reflected = reflect(r_in.direction(), rec.normal);
        float ni_over_nt;
        attenuation = vec3(1.0, 1.0, 1.0);
        vec3 refracted;

        float reflect_prob; //反射概率
        float cosine;

        if (dot(r_in.direction(), rec.normal) > 0) //从里到外，即入射向量在法向量另外一侧的情况
        {
            outward_normal = -rec.normal;   //对法向量取反
            ni_over_nt = ref_idx;           
            cosine = ref_idx * dot(r_in.direction(), rec.normal) / r_in.direction().length();
            //不知道为什么这里要乘一个ref_idx
        }
        else    //从外到里，即入射向量在法向量同一侧
        {
            outward_normal = rec.normal;    //法向量不变
            ni_over_nt = 1.0 / ref_idx;     
            cosine = -dot(r_in.direction(), rec.normal) / r_in.direction().length();
        }

        if (refract(r_in.direction(), outward_normal, ni_over_nt, refracted))
        {
            reflect_prob = schlick(cosine, ref_idx);
        }
        else    //若无折射，则全反射
        {
            reflect_prob = 1.0;
        }

        if (random_double() < reflect_prob)
        {
            scattered = ray(rec.p, reflected);
        }
        else
        {
            scattered = ray(rec.p, refracted);
        }

        return true;
    }

    float ref_idx;
};

场景使用三个电介质模型：

	list[0] = new sphere(vec3(0, 0, -1), 0.4, new dielectric(1.5));
	list[1] = new sphere(vec3(0, -100.5, -1), 100, new lambertian(vec3(0.0, 1.0, 1.0)));//new
	list[2] = new sphere(vec3(1, 0, -1), 0.3, new dielectric(0.5));    //new
	list[3] = new sphere(vec3(-1, 0, -1), 0.3, new dielectric(5.0));    //new