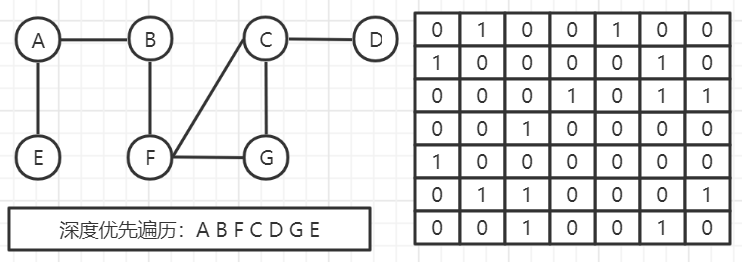
深度优先搜索

在这里插入图片描述

与广度优先搜索不同，深度优先搜索(Depth-First-Search，DFS)类似于树的先序遍历。如其名称中所暗含的意思一样，这种搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图。
它的基本思想如下：首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点
$w_1 w 1 ，再访问与 w 1 w_1 w 1 邻接且未被访问的任一顶点 w 2 w_2 w 2 …重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直至图中所有顶点均被访问过为止。$

代码实现(邻接矩阵法)

#include<stdio.h>
#include<malloc.h>
#define MaxVertenNum 100 //顶点数目的最大值
#define NodeNum 7 //顶点个数
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //存放顶点信息
typedef struct
{
	VertexType Vex[MaxVertenNum]; //顶点表
	EdgeType Edge[MaxVertenNum][MaxVertenNum]; //邻接矩阵
	int vexnum, edgenum; //图的当前顶点数和边数
}MGraph;

void InitG(MGraph& g) //初始化
{
	int i, j;
	for (i = 0; i < MaxVertenNum; i++)
	{
		g.Vex[i] = '\0';
	}
	for (i = 0; i < MaxVertenNum; i++)
		for (j = 0; j < MaxVertenNum; j++)
			g.Edge[i][j] = 0;
	g.vexnum = NodeNum;
}

void CreateVex(MGraph &g) //创建顶点信息
{
	VertexType ch;
	printf("输入图的顶点：");
	for (int i = 0; i < g.vexnum; i++)
	{
		scanf("%c", &ch);
		g.Vex[i] = ch;
	}
}

void CreateEdge(MGraph& g) //创建邻接矩阵信息
{
	EdgeType b;
	int i, j = 0;
	printf("输入邻接矩阵信息：\n");
	for (i = 0; i < g.vexnum; i++)
		for (j = 0; j < g.vexnum; j++)
		{
			scanf("%d", &b);
			g.Edge[i][j] = b;
		}
}

void Info(MGraph& g) //图的顶点数和边数
{
	int count = 0;
	for (int i = 0; i < g.vexnum; i++)
		for (int j = 0; j < g.vexnum; j++)
			if (g.Edge[i][j] == 1) count++;
	g.edgenum = count / 2;
}

int CountDegree(MGraph g, VertexType point) //统计每个顶点的度
{
	int j, k, count = 0;
	for (int i = 0; i < g.vexnum; i++)
		if (g.Vex[i] == point) j = i;
	for (int k = 0; k < g.vexnum; k++) if (g.Edge[j][k] == 1) count++;
	return count;
}

void PrintG(MGraph g) //输出各顶点的连接情况
{
	int i, j;
	for (i = 0; i < g.vexnum; i++)
	{
		for (j = 0; j < g.vexnum; j++)
			if (g.Edge[i][j] == 1) printf("%c->%c		", g.Vex[i], g.Vex[j]);
		printf("\n");
	}
}

int FirstNeighbor(MGraph g,VertexType x) //求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1。
{
	int i, j;
	for (i = 0; i < g.vexnum; i++)
		if (x == g.Vex[i]) j = i;
	if (j >= g.vexnum) return -1; //图中不存在值为x的顶点
	else
	{
		for (i = 0; i < g.vexnum; i++)
			if (g.Edge[j][i] == 1) return i; //返回顶点号
		if (i >= g.vexnum) return -1; //x没有邻接点
	}
}

int NextNeighbor(MGraph g, VertexType x, VertexType y)
{
	int i, j, k;
	for (i = 0; i < g.vexnum; i++)
	{
		if (g.Vex[i] == x) j = i;
		if (g.Vex[i] == y) k = i;
	}
	if (j >= g.vexnum || k >= g.vexnum) return false; //不存在顶点x或顶点y
	else
	{
		for (i = k+1; i < g.vexnum; i++)
		{
			if (g.Edge[j][i] == 1) return i; //返回顶点号
		}
		if (i >= g.vexnum) return -1; //x没有邻接点
	}
}

void PrintMatrix(MGraph g) //输出邻接矩阵
{
	int i, j;
	printf("输出邻接矩阵：\n");
	for (i = 0; i < g.vexnum; i++)
		printf("\t%c", g.Vex[i]);
	printf("\n");

	for (i = 0; i < g.vexnum; i++)
	{
		printf("%c", g.Vex[i]);
		for (j = 0; j < g.vexnum; j++)
			printf("\t%d", g.Edge[i][j]);
		printf("\n");
	}
	printf("\n");
}

bool visited[MaxVertenNum]; //访问标记数组
void DFS(MGraph g, VertexType ch) //从顶点出发，深度优先遍历图
{
	int i, j;
	for (i = 0; i < g.vexnum; i++)
		if (g.Vex[i] == ch) j = i;
	printf("%c ", ch); //访问顶点
	visited[j] = true; //设已访问标记
	for (i = FirstNeighbor(g, g.Vex[j]); i >= 0; i = NextNeighbor(g, g.Vex[j], g.Vex[i]))
		if (!visited[i]) DFS(g, g.Vex[i]); //尚未访问的邻接顶点
}

void DFSTraverse(MGraph g) //对图G进行深度优先遍历
{
	int i;
	for (i = 0; i < g.vexnum; i++) visited[i] = false; //初始化访问标记数据
	for (i = 0; i < g.vexnum; i++) //从0号顶点出发，深度优先遍历图G
		if (!visited[i]) DFS(g, g.Vex[i]);
}

int main()
{
	MGraph g;
	VertexType Vex[MaxVertenNum];
	EdgeType Edge[MaxVertenNum][MaxVertenNum];
	InitG(g);
	CreateVex(g);
	CreateEdge(g);

	Info(g);
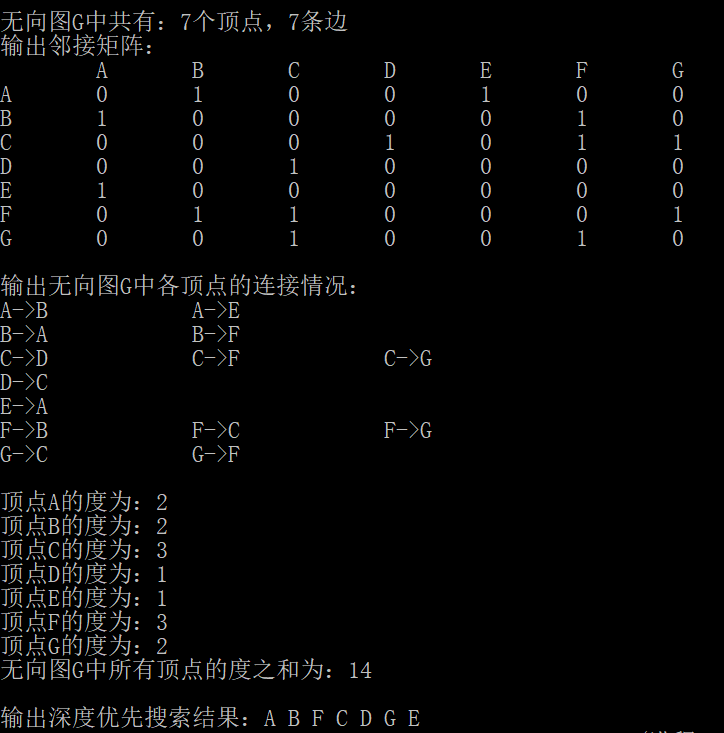
	printf("\n无向图G中共有：%d个顶点，%d条边\n", g.vexnum, g.edgenum);

	PrintMatrix(g);

	printf("输出无向图G中各顶点的连接情况：\n");
	PrintG(g);
	printf("\n");

	int sumdegree = 0, i;
	for (i = 0; i < g.vexnum; i++)
	{
		int degree;
		degree = CountDegree(g, g.Vex[i]);
		printf("顶点%c的度为：%d\n", g.Vex[i], degree);
		sumdegree = sumdegree + degree;
	}
	printf("无向图G中所有顶点的度之和为：%d\n", sumdegree);

	printf("\n输出深度优先搜索结果：");
	DFSTraverse(g);

	return 0;
}

运行结果

程序分析

空间复杂度：来自函数调用栈，最坏情况，递归深度为O(|V|)；最好情况，O(1)。
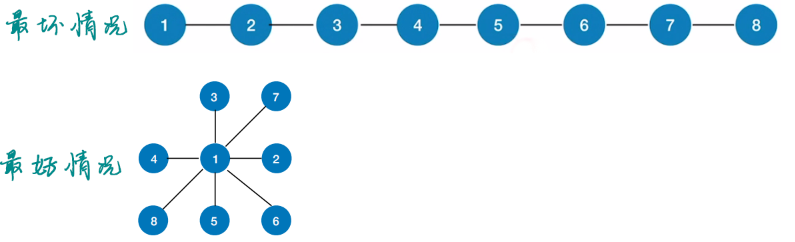
时间复杂度=访问各结点所需时间+探索各条边所需时间。
采用邻接矩阵存储方式时：访问|V|个顶点需要O(|V|)的时间，查找每个顶点的邻接点都需要O(|V|)的时间，而总共有|V|个顶点，因此

时间复杂度=O(|V|
$^2 2 ) 。$

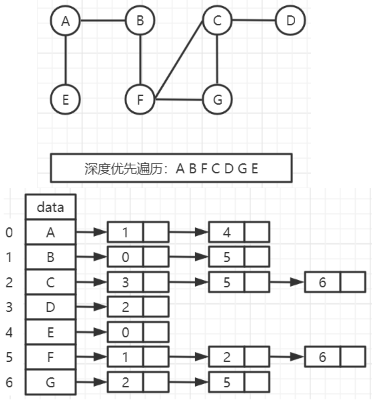
代码实现(邻接表法)

#include<stdio.h>
#include<malloc.h>
#define MaxVertexNum 100
#define NodeNum 7 //顶点数
typedef char VertexType;

//图的类型声明
typedef struct ArcNode
{
	int adjvex; //该边的邻接点编号
	struct ArcNode* nextarc; //指向下条边的指针
	//int weight; //该边的相关信息，如权值
}ArcNode; //边结点的类型

typedef struct VNode
{
	VertexType data; //顶点信息
	ArcNode* firstarc; //指向第一个边结点
}VNode;

typedef struct
{
	VNode adjlist[MaxVertexNum]; //邻接表的头结点数组
	int vexnum, edgenum; //图中的顶点数和边数
}AdjGraph; //完整的图邻接表类型

void InitG(AdjGraph& g)
{
	int i;
	for (i = 0; i < MaxVertexNum; i++)
	{
		g.adjlist[i].data = '\0';
		g.adjlist[i].firstarc = NULL;
	}
	g.vexnum = NodeNum;
}

void CreateVNde(AdjGraph& g)
{
	int i;
	char ch;
	printf("输入顶点信息：");
	for (i = 0; i < g.vexnum; i++)
	{
		scanf("%c", &ch);
		g.adjlist[i].data = ch;
		g.adjlist[i].firstarc = NULL;
	}
}

void CreateANode(AdjGraph& g, VertexType ch, int num)
{
	ArcNode* p, * r = g.adjlist[0].firstarc;
	int i, j, k;
	while (num--)
	{
		p = (ArcNode*)malloc(sizeof(ArcNode));
		p->nextarc = NULL;
		printf("输入顶点的编号：");
		scanf("%d", &i);
		for (j = 0; j < g.vexnum; j++)
			if (g.adjlist[j].data == ch) k = j;
		if (i != k)
		{
			p->adjvex = i;
			if (g.adjlist[k].firstarc == NULL)
			{
				g.adjlist[k].firstarc = p;
				r = p;
			}
			else
			{
				r->nextarc = p;
				r = p;
			}
		}
	}
}

int FirstNeighbor(AdjGraph& g, VertexType x) 
//求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回 - 1
{
	int i, j;
	for (i = 0; i < g.vexnum; i++)
		if (g.adjlist[i].data == x) j = i;
	if (j >= g.vexnum) return -1; //图中不存在x
	ArcNode* p = g.adjlist[j].firstarc;
	if (p == NULL) return -1; //若x没有邻接点
	else return p->adjvex; //返回顶点号
}

int NextNeighbor(AdjGraph& g, VertexType x, VertexType y) 
//求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回 - 1
{
	int i, j, k;
	for (i = 0; i < g.vexnum; i++)
	{
		if (g.adjlist[i].data == x) j = i;
		if (g.adjlist[i].data == y) k = i;
	}
	if (j >= g.vexnum || k >= g.vexnum) return -1; //不存在顶点x或顶点y
	else
	{
		ArcNode* p = g.adjlist[j].firstarc;
		while (p != NULL)
		{
			if (p->adjvex == k)
			{
				if (p->nextarc != NULL) return p->nextarc->adjvex;
				else return -1;
			}
			else p = p->nextarc;
		}
	}
}

void CountDegree(AdjGraph &g)
{
	ArcNode* p;
	int sumdegree = 0;
	printf("输出各顶点的度：\n");
	for (int i = 0; i < g.vexnum; i++)
	{
		p = g.adjlist[i].firstarc;
		int degree = 0;
		while (p != NULL)
		{
			degree++;
			p = p->nextarc;
		}
		sumdegree += degree;
		printf("顶点%c的度为：%d\n", g.adjlist[i].data, degree);
	}
	printf("无向图G中所有顶点的度之和为：%d", sumdegree);
	g.edgenum = sumdegree / 2;
}

void PrintG(AdjGraph g)
{
	int i;
	ArcNode* p;
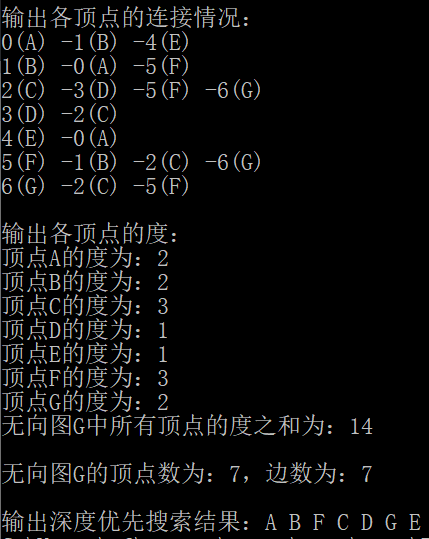
	printf("输出各顶点的连接情况：\n");
	for (i = 0; i < g.vexnum; i++)
	{
		p = g.adjlist[i].firstarc;
		printf("%d(%c) ", i, g.adjlist[i].data);
		while (p != NULL)
		{
			printf("-%d(%c) ", p->adjvex, g.adjlist[p->adjvex].data);
			p = p->nextarc;
		}
		printf("\n");
	}
	printf("\n");
}


bool visited[MaxVertexNum]; //访问标记数组
void DFS(AdjGraph g, VertexType ch)
{
	int i, j;
	for (i = 0; i < g.vexnum; i++)
		if (g.adjlist[i].data == ch) j = i;
	printf("%c ", ch); //访问顶点
	visited[j] = true; //设已访问标记
	for (i = FirstNeighbor(g,g.adjlist[j].data); i >= 0; i = NextNeighbor(g, g.adjlist[j].data, g.adjlist[i].data))
		if (!visited[i]) DFS(g, g.adjlist[i].data); //尚未访问的邻接顶点
}

void DFSTraverse(AdjGraph g) //对G进行深度优先遍历
{
	int i;
	for (i = 0; i < g.vexnum; i++) visited[i] = false; //初始化已访问标记数据
	for (i = 0; i < g.vexnum; i++) //从0号顶点开始遍历
		if (!visited[i]) DFS(g, g.adjlist[i].data);
}

int main()
{
	AdjGraph g;
	VertexType ch;
	int i, num;
	ArcNode* p;

	InitG(g);
	CreateVNde(g);
	printf("\n");
	for (i = 0; i < g.vexnum; i++)
	{
		printf("创建顶点%c的边结点\n", g.adjlist[i].data);
		printf("输入要创建的边结点的个数：");
		scanf("%d", &num);
		CreateANode(g, g.adjlist[i].data, num);
		printf("\n");
	}

	PrintG(g);

	CountDegree(g);
	printf("\n");
	printf("\n无向图G的顶点数为：%d，边数为：%d\n", g.vexnum, g.edgenum);

	printf("\n输出深度优先搜索结果：");
	DFSTraverse(g);

	return 0;
}

运行结果

程序分析

空间复杂度：来自函数调用栈，最坏情况，递归深度为O(|V|)；最好情况，O(1)。
时间复杂度=访问各结点所需时间+探索各条边所需时间。
采用邻接表存储方式时：访问|V|个顶点需要O(|V|)的时间，查找各个顶点的邻接点共需要O(|E|)的时间，

时间复杂度= O(|V|+|E|)

。

原文链接：https://blog.csdn.net/weixin_42071236/article/details/120077347

深度优先搜索

代码实现(邻接矩阵法)

运行结果

程序分析

代码实现(邻接表法)

运行结果

程序分析

你可能也喜欢