每日一题，坚持使我强大

今日份快乐：洛谷 P1219

传送门

明天份快乐：codeforces 5C (括号匹配)

传送门

题目大意

在 n * n 的棋盘上放置 n 个皇后，使得她们不能相互攻击，问一共有多少种方案，并输出前三组方案的具体坐标。

皇后会攻击和她在同一行，同一列和同一条对角线上的其他皇后，也就是说，任意两个皇后不能共线。

分析

先解释一下输出三组坐标的方法：拿一个简单的 4*4 的样例来看，如图



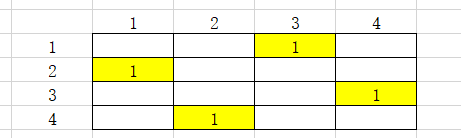
这是四皇后的一种方案，第一列的皇后的横坐标为 2 ，第二列的皇后的横坐标为 4 ，第三列的皇后的横坐标为 1 ，第一列的皇后的横坐标为 3。则这个方案皇后的坐标为输出为：2 4 1 3，也就是，

输出每列皇后的横坐标

。

八皇后问题是一个典型的搜索问题，我们先来补充一点基础的知识(国际象棋的黑白格 and 对角线和坐标的关系)，

干货

（

知识点传送门

）。

我们直接来讲搜索的过程，我们先在第一列的不同位置放置皇后：在第一列放置好一个皇后时，我们尝试在第二列不同的位置放置皇后，在第三列放置好以后，再尝试……直到第 n 列也可放置好皇后时，这就是一组可行的方案。

说一些细节的事情：

• one：要判断我们放的皇后是不是共线，我们可以对以前放置的皇后的所在的行和对角线(这里就用到了坐标与对角线的关系)进行标记。
• two：我们在不断的尝试放置皇后时，要回到上一层，肯定要取消掉当前点的标记。取消当前点的标记并返回上一层的这个过程就叫
  
  回溯
  
  ，回溯可以避免上一次的标记对下面搜索的影响。
  
  eg：在 4 * 4 的棋盘中，当我们标记完（2，3）时，发现第三列根本无法放置皇后，我们就要回到上一层的（1，1）。这时我们就要去掉（2，3）这个点的标记，到（1，1）去尝试向第二列的其他点放置皇后。
  
  

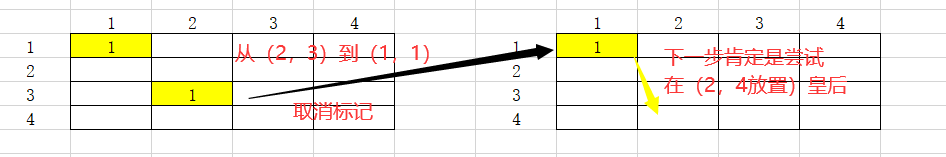
搜索的细节看代码

代码

#include <bits/stdc++.h>
using namespace std;

int hang[105] = {0};	// 标记行
int zhu[105]  = {0};	// 标记主对角线
int ci[105]  = {0};	// 标记次对角线
int res[20];		// 存每组的坐标
int num = 0;		// 输出坐标组数
int ans = 0;		// 方案总数
int n;

void pr(){		//输出前三组的坐标
	num++;
	for(int i = 1; i <= n; i++) cout << res[i] << " ";
	cout << endl;
}

void DFS(int x){ 			
	if(x > n){				// 找到如果走到第 n+1 列，说明前 n 列已经都放下了皇后 
		ans++;				// 方案数 +1 
		if(num < 3) pr();		// 看是不是前三组答案 
		return;
	}
	
	for(int y = 1; y <= n; y++){
		if(hang[y]) continue;				// 同一行	
		if(zhu[x - y + n]) continue;			// 同一条主对角线
		if(ci[x + y]) continue;				// 同一条次对角线 
		hang[y] = zhu[x - y + n] = ci[x + y] = 1;	// 标记这个点在的行和对角线 
		res[x] = y;					// 纪录这个点 
		DFS(x+1);					// 搜索 
		hang[y] = zhu[x - y + n] = ci[x + y] = 0;	// 回溯 
	}
}

int main() {

	ios::sync_with_stdio(false);
	
	cin >> n;
	
	DFS(1);		// 从第一列开始搜索
	
	cout << ans << endl;
	
    return 0;
}

欢迎大佬指错