1 欧式距离
欧氏距离(Euclidean distance)也称欧几里得度量、欧几里得度量,是一个通常采用的距离定义,它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离的就是两点之间的距离。
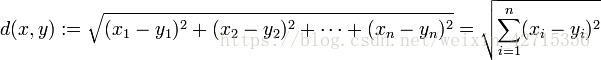
**缺点:**就大部分统计问题而言,欧氏距离是不能令人满意的。(每个坐标对欧氏距离的贡献是同等的。当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。它将样品的不同属性(即各指标或各变量)之间的差别等同看待,这一点有时不能满足实际要求。没有考虑到总体变异对距离远近的影响。
2 曼哈顿距离
曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基所创词汇,是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和
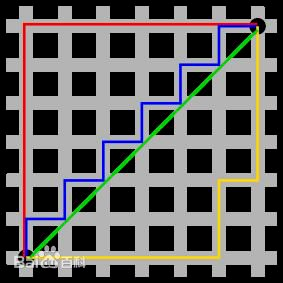
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。高纬度曼哈顿距离计算公式如下.
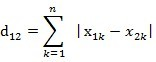
曼哈顿距离的一个优点是计算速度快
他的应用例如在西洋棋盘当中.
3 切比雪夫距离
两个高维度向量中,每个维度之差绝对值的最大值.例如两个i维的向量
x
1
(
x
11
,
x
12
.
.
.
.
x
1
n
)
,
x
2
(
x
21
,
x
22
,
.
.
.
x
2
n
)
x_1(x_{11},x_{12}….x_{1n}), x_2(x_{21},x_{22},…x_{2n})
x
1
(
x
1
1
,
x
1
2
.
.
.
.
x
1
n
)
,
x
2
(
x
2
1
,
x
2
2
,
.
.
.
x
2
n
)
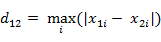
4 闵可夫斯基距离(Minkowski Distance)
闵氏距离不是一种距离,而是一组距离的定义。
(1) 闵氏距离的定义
两个n维变量
a
(
x
11
,
x
12
,
…
,
x
1
n
)
a(x_{11},x_{12},…,x_{1n})
a
(
x
1
1
,
x
1
2
,
…
,
x
1
n
)
与
b
(
x
21
,
x
22
,
…
,
x
2
n
)
b(x_{21},x_{22},…,x_{2n})
b
(
x
2
1
,
x
2
2
,
…
,
x
2
n
)
间的闵可夫斯基距离定义为:
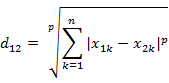
其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
(2)闵氏距离的缺点
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
举个例子:二维样本(身高,体重),其中身高范围是150~190, 而体重的范围是60 ~ 100,有三个样 本:a(180,50),b(190,50),c(180,60)。那么a与b之间的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之 间的闵氏距离,但是身高的10cm真的等价于体重的10kg么?因此用闵氏距离来衡量这些样本间的相似度很有问题。
简单说来,闵氏距离的缺点主要有两个:(1)将各个分量的量纲(scale),也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布(期望,方差等)可能是不同的
。
5 标准欧式距离
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路:既然数据各维分量的分布不一样,好吧!**那我先将各个分量都“标准 化”到均值、方差相等吧。**均值和方差标准化到多少呢?这里先复习点统计学知识吧,假设样本集X的均值(mean)为m,标准差(standard deviation)为s,那么X的“标准化变量”表示为:
X
∗
=
X
−
m
S
X^* = \frac{X-m}{S}
X
∗
=
S
X
−
m
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
经过简单的推导就可以得到两个n维向量
a
(
x
11
,
x
12
,
…
,
x
1
n
)
a(x_{11},x_{12},…,x_{1n})
a
(
x
1
1
,
x
1
2
,
…
,
x
1
n
)
与
b
(
x
21
,
x
22
,
…
,
x
2
n
)
b(x_{21},x_{22},…,x_{2n})
b
(
x
2
1
,
x
2
2
,
…
,
x
2
n
)
间的标准化欧氏距离的公式:
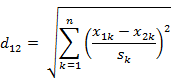
如果将方差的倒数看成是一个权重,这个公式可以看成是一种加权欧氏距离
6 马氏距离
有M个样本向量
X
1
X
m
X_1~X_m
X
1
X
m
,协方差矩阵记为S,均值记为向量
μ
\mu
μ
,则其中样本向量
X
到
μ
X 到\mu
X
到
μ
的马氏距离表示为:
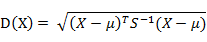
而其中向量
X
i
X_i
X
i
与
X
j
X_j
X
j
之间的马氏距离定义为:
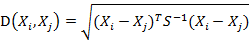
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了:
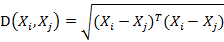
也就是欧氏距离了。
若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。
(2)马氏距离的优缺点:量纲无关,排除变量之间的相关性的干扰。
7 汉明距离
汉明距离的定义
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)。