前言

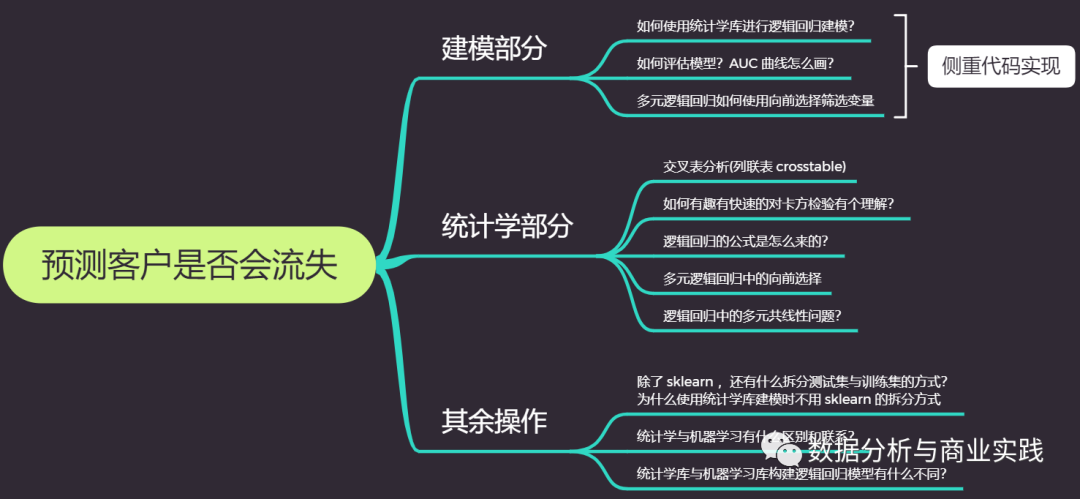
利用逻辑回归进行客户流失预警建模中涵盖了许多比较细的知识点，思维导图只展示了极小的一部分，相关知识点链接将穿插在文中。(源数据源代码空降文末获取)

数据探索

数据读入

churn = pd.read_csv('telecom_churn.csv', skipinitialspace=True)
churn.head() 
# 列比较多，显示不完

churn.info() # 发现数据都比较整洁

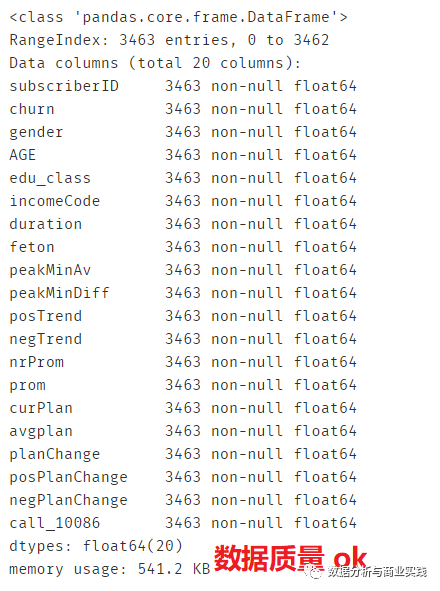
数据属性说明

数据探索

简洁版本，只是为了一元逻辑回归做的探索，毕竟实际情况中数据分析师们80%的时间可能都是用来清洗数据和结合具体业务来探索数据，所以探索数据方面并不是我们的侧重点。

churn 流失与否 是否与 posTrend 流量使用上升趋势有关 猜想：posTrend 为 1，即

流量使用有上升趋势时，更不容易流失

(用得越多越不容易流失)

交叉表分析

cross_table = pd.crosstab(index=churn.posTrend, columns=churn.churn, 
                          margins=True)
      # margins 就是为了在最后一行和最后一类后面添加个汇总的 all
cross_table

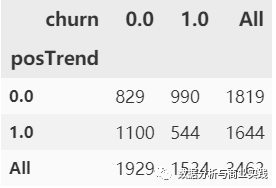
# 转化成百分比的形式
def perConvert(ser):
    return ser/float(ser[-1])

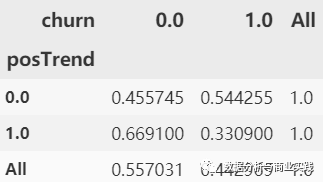
cross_table.apply(perConvert, axis='columns') 
    # axis=1 也可以写成 axis='columns', 表示对列使用这个函数
    
# 发现的确如我们所想，流量使用有上升趋势的时候，流失的概率会下降

卡方检验

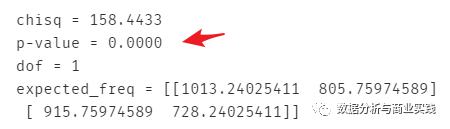
print("""chisq = %6.4f
p-value = %6.4f
dof = %i
expected_freq = %s""" % stats.chi2_contingency(observed=cross_table.iloc[:2, :2]))
# iloc 是因为 cross_table 添加了 margin 参数，也就是在最后一行和最后一列都显示 all，
 ## 卡方检验的时候我们只需要传入类别列即可，无需总列
# 发现检验结果还是比较显著的，说明 posTrend 这个变量有价值

建模流程

一元逻辑回归

拆分测试集与训练集

train = churn.sample(frac=0.7, random_state=1234).copy()
test = churn[~ churn.index.isin(train.index)].copy() 
# ~ 表示取反，isin 表示在不在，这个知识点 pandas 非常常用
print(f'训练集样本量：{len(train)}, 测试集样本量：{len(test)}')
# 训练集样本量：2424, 测试集样本量：1039

statsmodels 库进行逻辑回归

# glm: general linear model - 也就是逻辑回归的别称：广义线性回归
lg = smf.glm(formula='churn ~ duration', data=churn,
            family=sm.families.Binomial(sm.families.links.logit)).fit()
            ## family=sm .... logit 这一大行看似难，其实只要是统计学库进行逻辑回归建模，
             ## 都是这样建，families 族群为 Binomial，即伯努利分布(0-1 分布)
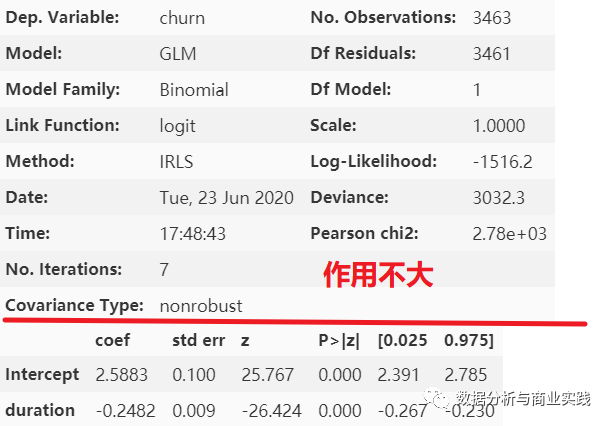
lg.summary()
#  下面的一大个表中，只有这些还稍微有点价值，发现两个变量都挺显著，
#     呈现一定的负相关关系，可以先简单理解为，每增加一个单位，流失的概率就下降一点
#           coef stderr   z     P>|z| [0.025 0.975]
# Intercept 3.0207 0.116 26.078 0.000 2.794 3.248
# duration -0.2488 0.010 -25.955 0.000 -0.268 -0.230

使用建模结果进行预测

# 预测流失的可能性
train['proba'] = lg.predict(train)
test['proba'] = lg.predict(test)

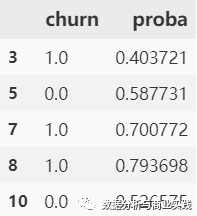
test[['churn', 'proba']].head() # 我们可以假设 proba > 0.5 就算流失，
# 即如果 churn=1，proba > 0.5，则表示预测正确，当然，这个 proba 需要根据业务实际情况来定

# 以 proba > 0.5 就设为流失作为预测结果
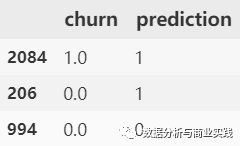
test['prediction'] = (test['proba'] > 0.5)*1 
        # 最后 *1 是为了把 True 和 False 转化成 1 和 0
test[['churn', 'prediction']].sample(3)

检验预测结果

# 计算一下模型预测的准度如何
acc = sum(test['prediction'] == test['churn']) / np.float(len(test))
print(f'The accuracy is: {acc}') 
## 精度不错：The accuracy is: 0.7651588065447545

# sklearn 包绘制 Python 专门用来评估逻辑回归模型精度的 ROC 曲线
import sklearn.metrics as metrics
## 测试集的 roc 曲线
fpr_test, tpr_test, th_test = metrics.roc_curve(test.churn, test.proba)
## 训练集的 roc 曲线
fpr_train, tpr_train, th_train = metrics.roc_curve(train.churn, train.proba)

plt.figure(figsize=[3, 3])
plt.plot(fpr_test, tpr_test, 'b--')
plt.plot(fpr_train, tpr_train, 'r--')
plt.title('ROC curve'); plt.show()
print(f'AUC = {metrics.auc(fpr_test, tpr_test)}')

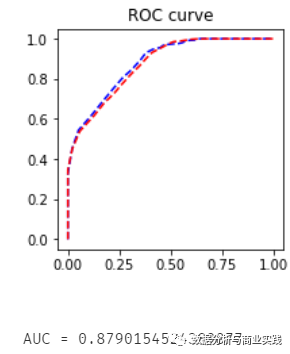
建模结果越靠近左上角越好，模型精度比较高。

多元逻辑回归

逐步向前法筛选变量

当然，这里的变量还不算特别特别多，还可以使用分层抽样，假设检验，方差分析等方法筛选，这里不用多解释了。逻辑回归的逐步向前法已有优秀前人的轮子，直接拿来用即可。篇幅原因就不完全展示了。文末获取源数据与含有详细注释的源代码

def forward_select(data, response):
  """略，文末获取源数据与含有详细注释的源代码"""

# 待放入的变量，除了 subsriberID 没用外，其他都可以放进去看下
candidates = churn.columns.tolist()[1:] 
data_for_select = train[candidates]
# 多元逻辑回归与多元线性回归的向前选择还是有些许不同的
lg_m1 = forward_select(data=data_for_select, response='churn')
lg_m1.summary()

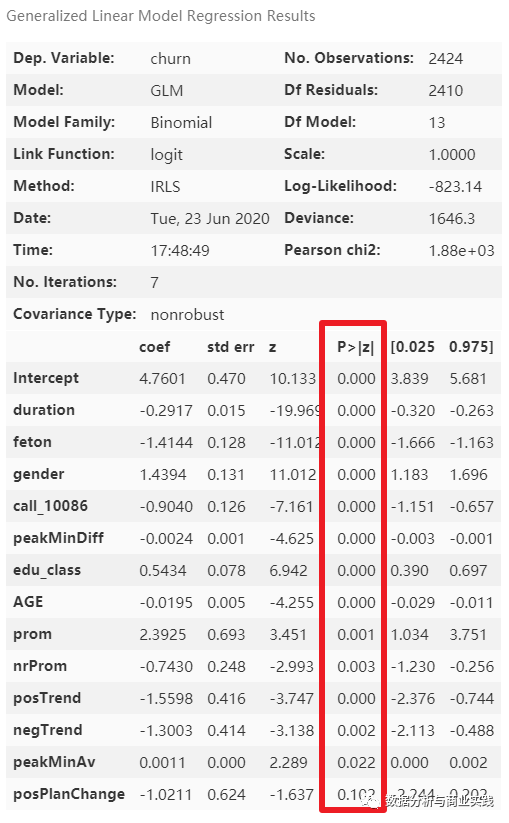
print(f'原来有 {len(candidates)} 个变量')
print(f'筛选剩下 {len(lg_m1.params.index.tolist())} 个(包含 intercept 截距项)。')

# 原来有 19 个变量,筛选剩下 14 个(包含 intercept 截距项)。

方差膨胀因子检测

多元逻辑回归中也会存在多元共线性的干扰，其具体含义可查看如下文章：

多元共线性检测 — 方差膨胀因子

def vif(df, col_i):
    from statsmodels.formula.api import ols
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)

after_select = lg_m1.params.index.tolist()[1:] # Intercept 不算
exog = train[after_select]

for i in exog.columns:
    print(i, '\t', vif(df=exog, col_i=i))
# 按照一般规则，大于10的就算全部超标，通常成对出现，只需要删除成对出现的一个即可。
 ## 这里我们挑成对出现中较大的删除

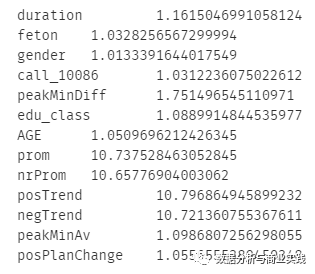
# 删除 prom，posTrend
drop = ['prom', 'posTrend']
final_left = [x for x in after_select if x not in drop]

# 再来一次方差膨胀因子检测
exog = train[final_left]
for i in exog.columns:
    print(i, '\t', vif(df=exog, col_i=i))

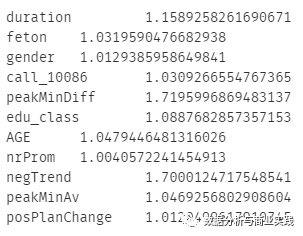
再次进行建模与模型精度的检验

重复一元逻辑回归的步骤即可。

本公众号后续将继续更新数据科学与商业实践中常见的案例

案例实战 | Python 实现 RFM 模型
一行代码实现异常值检验常用的两种方法
注：相关数据源和超详细的代码(python，Jupyter Notebook 版本 + 详细注释)已经整理好，在 “ 数据分析与商业实践 ” 公众号后台回复 “ 逻辑流失 ” 即可获取。