语义分析和中间代码生成

中间语言

在这里插入图片描述

后缀式

在这里插入图片描述

图表示法

在这里插入图片描述

三地址代码

在这里插入图片描述

赋值语句的翻译

在这里插入图片描述

下面给出一个以三地址代码为中间语言的赋值语句的S属性文法

那个 || 表示连接上不是表示或

比如 S->id := E 的语义规则表示 S的三地址代码是由E的三地址代码再连接上一个 gen函数返回值

gen返回的是一段三地址代码

E.place = newtemp

表示先产生一个临时变量用于存放之后的运算结果，然后存储到E.place中

在这里插入图片描述

lookup查找在符号表中是否出现

newtemp 是临时变量，用于存储以后的运算结果

E.place 放的是运算结果的名字 / 地址

最后 E -> id 表示的是 E的结果单元 E.place 就是变量 id的结果单元，单独一个变量，没有三地址代码，所以是 E.code = ’ ’

所以，他的语义动作就是调用 lookup函数，在符号表中查找变量标识符 id , 如果找到了,lookup就返回变量标识符的入口

数组元素引用的翻译

编译程序会对数组名和下标表达式列表进行分析和翻译，在目标程序或中间语言程序插入计算出要访问的数组元素的地址的代码

在这里插入图片描述

编译程序会生成两组计算数组元素地址的代码，一部分是红色的可变部分的代码，一部分是蓝色的不变部分的代码

不变部分所涉及的信息在数组声明的时候就确定了

Elist 表示表达式列表，放在 [ ]中，作为下标表达式列表

id[Elist] 叫做数组元素的引用，有时也叫做下表变量

在这里插入图片描述

Elist.ndim 表示处理到了第几维

在这里插入图片描述

带数组元素的赋值语句的翻译

在这里插入图片描述

L.place ’ [ ’ L.offset ’ [ ’ ’ := ’ E.place

这条语句赋值号的左边是一个变址访问，利用 L.place 记录的地址计算的不变部分和 L.offset记录的可变部分做变址访问，访问到的单元就是接受E.place 结果的数组元素

在这里插入图片描述

Elist.place 记录从左到右分析完的下标列表，计算出来的可变部分的前一阶段的值，这个值总是随着下标列表的不断识别分析，从左到右，逐步的做乘法加法，乘法加法累计计算出来，总是把 Elist 乘以这一维的个数，再加上这一维表达式的值，就这样像滚雪球一样把可变部分的值计算出来

最后把数组名表示符 id 的信息记录在 Elist.array 中

这就是数组元素分析，刚开始的语义动作

在这里插入图片描述

随着数组元素分析的进行，

假设我们现在处理到了第m 维

前面分析完的各种信息都在 Elist1 里面，现在第 m 维分析完了后内容到了 E

Elist1.place 就是前面 m-1 维的计算结果 ,是这一部分

在这里插入图片描述

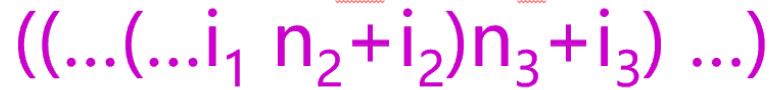
随着一维一维的分析，最终会分析完碰到右括号

Elist.array 记录了数组名，这个数组名就是那个首地址base

C 是数组声明时就确定了不变得常量部分(对应绿色部分)

在这里插入图片描述

类型转换

当程序中出现不同类型的值得运算时，编译器需要要么拒绝这种运算，要么产生有关类型转换的指令，使得最后目标代码中参与运算的数据类型是一致的

int* 表示整形的乘法

在这里插入图片描述

布尔表达式的翻译

i rop i 表示关系运算可以构成布尔表达式

rop 关系运算符，可以是 > , >= , <= , < , == ， <>（不等于）

在这里插入图片描述

在这里插入图片描述

数值表示法的翻译模式

在这里插入图片描述

在这里插入图片描述

emit 表示向输出文件发送一条指令

E1.place 里面放的是 E1 这一子表达式的运算结果的地址

带优化的布尔表达式翻译模式

在这里插入图片描述

E1.true = E.true 意思是 E1如果为真，那么就不要计算E2了，直接跳到 E为 true 的地方

E1为假，应该将来跳转执行到E2的代码，所以我们E1.false产生一个新标号，将来这个标号，就像 gen(E1.false ‘L’) 一样，要放到 E2的代码之前，标志着 E2 的开头，这样执行到如果 E1为 false ，程序就会跳转到这个标号这里

在这里插入图片描述

对于非运算，只要把 E1 和 E 的布尔属性翻转一下，无需改变其代码，就可以了

从根节点 E 开始，自上而下计算出整个语法树的布尔集成属性，每个节点都有一个（真标号，假标号）代表为真、假要跳转的地方

在这里插入图片描述

上图翻译是多遍扫描

建立语法树

计算各节点布尔值

自下而上生成代码

在这里插入图片描述

布尔表达式一边扫描翻译模式

那个 p 是四元式的标号，表示跳转到这个四元式

在这里插入图片描述

nextquard是输出序列中，下一个四元式的下标，将要放进输出序列的四元式的位置

一遍扫描最大的问题就是在其准备填入跳转时可能无法立即知道，需要分析完更大的语法单位才能回填

在这里插入图片描述

需要回填的分成两组，制作两个链表，一个是跳真的，一个是跳假的

实际上目前这个四元式，需要回填的那些，因为不知道要跳到哪，所以他第四个位置，跳转地址是空着的，我们就可以先利用起来，作为链表next指针用

最后的链尾放上0标志

同一个链表的中都是需要回填到同一个位置的

在这里插入图片描述

注意为了使我们的翻译模式能够和自下而上的语法分析结合起来，需要把语义动作放在产生式的右边，使得语义动作的执行时机能够统一到这规约完成的时候进行

对于 E – > E1 or E2 在扫描到or的时候，就知道 E1的fallist 的下一个地址位置就是 E2 的开头

所以在准备分析 E2前，需要有个语义动作，记录E2的地址

然后我们可以通过嵌入 ε 产生式，将那些嵌入在产生式中间的语义动作移动到产生式的后边

在这里插入图片描述

M.quard 记录了下一个将要生成的四元式的下标，也就是E2的第一个四元式的下标

之所以 esclispe 规约到 M 是为了获得一个执行语义动作的时机，把E2的第一个四元式的位置记录下来

我们使用的是自下而上的语法分析，当我们要设计翻译模式时，我们假设这个产生式已经分析完了

在这里插入图片描述

控制语句

在这里插入图片描述

if语句的属性文法

在这里插入图片描述

while语句的属性文法

S,begin 是综合属性

S.next 是继承属性

E.true E.false 都是继承属性

在这里插入图片描述

控制语句的属性计算示例

在这里插入图片描述

每个符号都给一个 (S.begin,S.next) 的标识或者是 (E.true, E.false)

对于S 只有是个循环语句的时候才会用到 S.begin ，不是循环这里填 –

在这里插入图片描述

一遍扫描翻译控制语句

在这里插入图片描述

L表示的是由分号分割的S的列表，也就是语句列表

M的语义动作就是记录下一个四元式的下标，把他记录到 M.quard属性里面

N的动作是产生 S1 和 S2之间的跳转指令的动作，使得执行完S1之后可以执行 if then else 的后面的语句，但是这个时候还不知道if then else后面的语句的地址是什么，所以我们需要产生一个回填链表，等到以后合适的时机回填，这个链表就只有一个四元式， emit(j,-,-,-)那个目的地址还不知道，等待以后回填

在这里插入图片描述

当分析碰到分号时，应该将分号前所有语句中，也就是说这个L当中的需要回填的四元式可以回填了，因为如果分号前还有一些四元式需要回填的，那么一定是去这些语句的后继语句的，而此时可以确定，这些所谓的后继语句就是马上要开始分析的分号后面的S的代码

在这里插入图片描述