1. 方阵的行列式

det(A)：求方阵A所对应的行列式的值

%A的逆的行列式等于A的行列式的倒数
>> format rat
>> A=[1,3,2;-3,2,1;4,1,2];
>> det(inv(A))
ans =
       1/11    
>> 1/det(A)
ans = 
       1/11

2. 矩阵的秩

矩阵线性无关的行数或列数称为矩阵的秩

rank(A)：求矩阵A的秩

e.g.求3~20阶魔法阵的秩
>> for n=3:20
r(n)=rank(magic(n));
%将秩存放在向量r中
end
>> bar(r)
%用r绘制直方图
>> grid on
%设置网格
>> axis([2,21,0,20])
%设置坐标轴范围

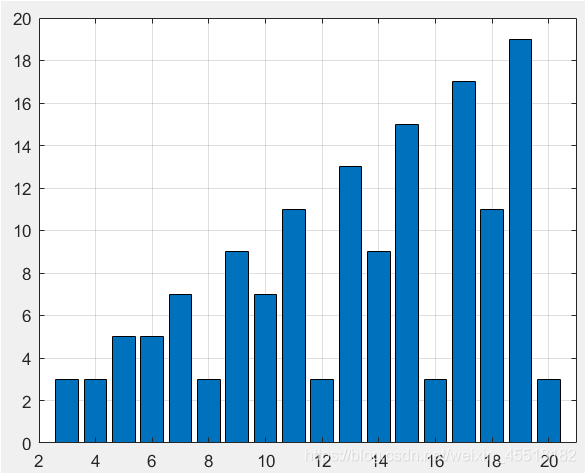
%奇数阶魔方阵秩为n，即奇数阶魔法阵为满秩矩阵



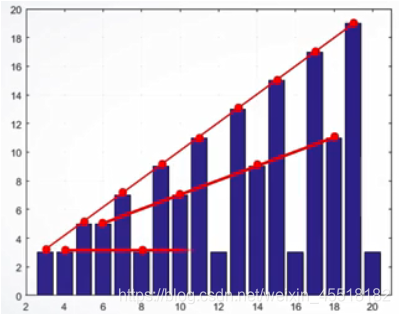
奇数阶魔方阵秩为n，即奇数阶魔方阵是满秩矩阵。

一重偶数阶魔方阵秩为n/2+2（n是2的倍数，但非4的倍数）；双重偶数阶魔方阵秩均为3（阶数是4的倍数）。

3. 矩阵的迹

即矩阵的对角线之和，也等于矩阵的特征值之和。

一般来说只有方阵才有特征值和特征向量。

trace(A)：求矩阵的迹

>> A=[1,3,2;-3,2,1;4,1,2];
>> b=trace(A)
b =
       5       
>> t=sum(diag(A))
t =
       5 
%e.g.用三种方法求矩阵的迹。
>> A=[1,3,2;-3,2,1;4,1,2];
>> trace(A)
ans =
       5       
>> sum(diag(A))
ans =
       5       
>> sum(eig(A))
ans =
       5       

补充：E＝eig(A)：求方阵A的全部特征值，构成列向量E

[V,D]=eig(A)：返回特征值构成的对角矩阵D，和矩阵V，其列为特征值对应的特征向量，A*V=V*D。

可见《4-矩阵的特征值和特征向量》

来自

https://blog.csdn.net/Intangilble/article/details/84313758?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1


来自

https://blog.csdn.net/u013457382/article/details/48270497

4. 矩阵和向量的范数

用来度量矩阵或向量在某种意义下的长度，范数一定是非负数。

5. 矩阵的条件数：描述矩阵性能的参数

矩阵A的条件数=A的范数*A的逆矩阵的范数。

条件数越接近于1，矩阵的性能越好，反之，矩阵的性能越差。


计算矩阵A的3种条件数的函数：


cond(A,1)：计算A的1-范数下的条件数

cond(A,2)或cond(A)：计算A的2-范数下的条件数

cond(A,inf)：计算A的∞-范数下的条件数


e.g.求2~10阶希尔伯特矩阵的条件数

>> for n=2:10
c(n)=cond(hilb(n));
end
>> format long
>> c'
%行矩阵转化为列矩阵
ans =
   1.0e+13 *
                   0
   0.000000000001928
   0.000000000052406
   0.000000001551374
   0.000000047660725
   0.000001495105864
   0.000047536735691
   0.001525757556663
   0.049315340455101
   1.602502816811318

随着阶数增加，希尔伯特矩阵的条件数不断增大，矩阵性能变差。