方差协方差以及协方差矩阵

协方差矩阵在统计学和机器学习中随处可见，一般而言，可视作

方差

和

协方差

两部分组成，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。本文旨在从几何角度介绍我们所熟知的协方差矩阵。

文章结构

方差和协方差的定义
从方差/协方差到协方差矩阵
多元正态分布与线性变换
协方差矩阵的特征值分解

1. 方差和协方差的定义

在统计学中，

方差

是用来度量

单个随机变量

的

离散程度

，而协方差则一般用来刻画

两个随机变量

的

相似程度

，其中，

方差

的计算公式为

$\sigma_x^2=\frac{1}{n-1}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2$

其中，
$n$
表示样本量，符号
$\bar{x}$
表示观测样本的均值，这个定义在初中阶段就已经开始接触了。

在此基础上，

协方差

的计算公式被定义为

$\sigma\left(x,y\right)=\frac{1}{n-1}\sum_{i=1}^{n}\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)$

在公式中，符号
$\bar{x},\bar{y}$
分别表示两个随机变量所对应的观测样本均值，据此，我们发现：方差
$\sigma_x^2$
可视作随机变量
$x$
关于其自身的协方差
$\sigma\left(x,x\right)$
.

2. 从方差/协方差到协方差矩阵

根据方差的定义，给定
$d$
个随机变量
$x_k,k=1,2,...,d$
，则这些

随机变量的方差

为

$\sigma({x_k},{x_k})=\frac{1}{n-1}\sum_{i=1}^n\left(x_{ki}-\bar{x}_k\right)^2,k=1,2,...,d$

其中，为方便书写，
$x_{ki}$
表示随机变量
$x_k$
中的第
$i$
个观测样本，
$n$
表示样本量，每个随机变量所对应的观测样本数量均为
$n$
。

对于这些随机变量，我们还可以根据协方差的定义，求出

两两之间的协方差

，即

$\sigma\left(x_m,x_k\right)=\frac{1}{n-1}\sum_{i=1}^n\left(x_{mi}-\bar{x}_m\right)\left(x_{ki}-\bar{x}_k\right)$

因此，

协方差矩阵

为

$\Sigma=\left[ \begin{array}{ccc}\sigma({x_1},{x_1}) & \cdots & \sigma\left(x_1,x_d\right) \\ \vdots & \ddots & \vdots \\ \sigma\left(x_d,x_1\right) & \cdots & \sigma({x_d},{x_d}) \\ \end{array} \right]\in\mathbb{R}^{d\times d}$

其中，对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，根据协方差的定义，我们可以认定：矩阵
$\Sigma$
为

对称矩阵

(symmetric matrix)，其大小为
$d\times d$
。

3. 多元正态分布与线性变换

假设一个向量
$\boldsymbol{x}$
服从均值向量为
$\boldsymbol{\mu}$
、协方差矩阵为
$\Sigma$
的多元正态分布(multi-variate Gaussian distribution)，则

$p\left(\boldsymbol{x}\right)=\left|2\pi\Sigma\right|^{-1/2}\exp\left(-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)^T\Sigma^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}\right)\right)$

令该分布的均值向量为
$\boldsymbol{\mu}=\boldsymbol{0}$
，由于指数项外面的系数
$\left|2\pi\Sigma\right|^{-1/2}$
通常作为常数，故可将多元正态分布简化为

$p\left(\boldsymbol{x}\right)\propto\exp\left(-\frac{1}{2}\boldsymbol{x}^T\Sigma^{-1}\boldsymbol{x}\right)$

再令
$\boldsymbol{x}=\left(y,z\right)^T$
，包含两个随机变量
$y$
和
$z$
，则协方差矩阵可写成如下形式：

$\Sigma=\left[ \begin{array}{cc}\sigma(y,y) & \sigma\left(y,z\right) \\ \sigma\left(z,y\right) & \sigma(z,z) \\ \end{array} \right]\in\mathbb{R}^{2\times 2}$

用

单位矩阵

(identity matrix)
$I$
作为协方差矩阵，随机变量
$y$
和
$z$
的

方差均为1

，则生成如干个随机数如图1所示。

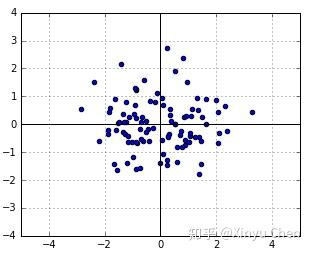
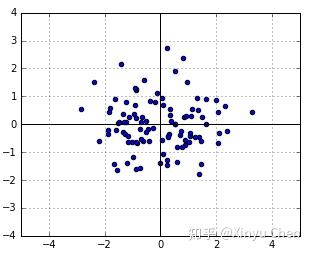
在生成的若干个随机数中，每个点的似然为

$\mathcal{L}\left(\boldsymbol{x}\right)\propto\exp\left(-\frac{1}{2}\boldsymbol{x}^T\boldsymbol{x}\right)$

对图1中的所有点考虑一个

线性变换

(linear transformation)：
$\boldsymbol{t}=A\boldsymbol{x}$
，我们能够得到图2.

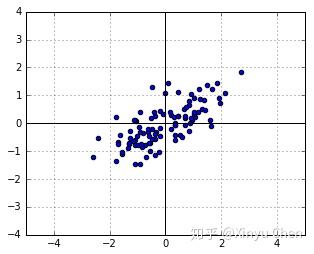
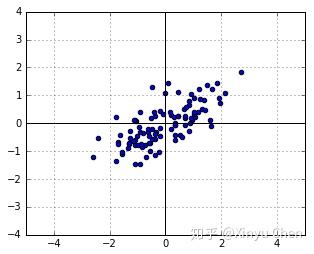
图2 经过线性变换的二元正态分布，先将图1的纵坐标压缩0.5倍，再将所有点逆时针旋转30°得到。

在线性变换中，矩阵
$A$
被称为

变换矩阵

(transformation matrix)，为了将图1中的点经过线性变换得到我们想要的图2，其实我们需要构造两个矩阵：

尺度矩阵

(scaling matrix)：

$S=\left[ \begin{array}{cc} s_y & 0 \\ 0 & s_z \\ \end{array} \right]$

旋转矩阵

(rotation matrix)

$R=\left[ \begin{array}{cc} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \\ \end{array} \right]$

其中，
$\theta$
为

顺时针旋转的度数

。

变换矩阵、尺度矩阵和旋转矩阵三者的关系式：

$A=RS$

在这个例子中，尺度矩阵为
$S=\left[ \begin{array}{cc} 1 & 0 \\ 0 & \frac{1}{2} \\ \end{array} \right]$
，旋转矩阵为
$R=\left[ \begin{array}{cc} \cos(-\frac{\pi}{6}) & -\sin(-\frac{\pi}{6}) \\ \sin(-\frac{\pi}{6}) & \cos(-\frac{\pi}{6}) \\ \end{array} \right]$
$=\left[ \begin{array}{cc} \frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \\ \end{array} \right]$
，故变换矩阵为

$A=RS=\left[ \begin{array}{cc} \frac{\sqrt{3}}{2} & \frac{1}{4} \\ -\frac{1}{2} & \frac{\sqrt{3}}{4} \\ \end{array} \right]$
.

另外，需要考虑的是，经过了线性变换，
$\boldsymbol{t}$

的分布是什么样子呢

？

将
$\boldsymbol{x}=A^{-1}\boldsymbol{t}$
带入前面给出的似然
$\mathcal{L}\left(\boldsymbol{x}\right)$
，有

$\mathcal{L}\left(\boldsymbol{t}\right)\propto\exp\left(-\frac{1}{2}\left(A^{-1}\boldsymbol{t}\right)^T\left(A^{-1}\boldsymbol{t}\right)\right)$

$=\exp\left(-\frac{1}{2}\boldsymbol{t}^T\left(AA^{T}\right)^{-1}\boldsymbol{t}\right)$

由此可以得到，多元正态分布的协方差矩阵为

$\Sigma=AA^{T}=\left[ \begin{array}{cc} \frac{\sqrt{3}}{2} & \frac{1}{4} \\ -\frac{1}{2} & \frac{\sqrt{3}}{4} \\ \end{array} \right]\left[ \begin{array}{cc} \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ \frac{1}{4} & \frac{\sqrt{3}}{4} \\ \end{array} \right]$
$=\left[ \begin{array}{cc} \frac{13}{16} & -\frac{3\sqrt{3}}{16} \\ -\frac{3\sqrt{3}}{16} & \frac{7}{16} \\ \end{array} \right]$
.

4. 协方差矩阵的特征值分解

回到我们已经学过的线性代数内容，对于任意对称矩阵
$\Sigma$
，存在一个

特征值分解(eigenvalue decomposition, EVD)

：

$\Sigma=U\Lambda U^T$

其中，
$U$
的每一列都是相互正交的特征向量，且是单位向量，满足
$U^TU=I$
，
$\Lambda$
对角线上的元素是从大到小排列的特征值，非对角线上的元素均为0。

当然，这条公式在这里也可以很容易地写成如下形式：

$\Sigma=\left(U\Lambda^{1/2}\right)\left(U\Lambda^{1/2}\right)^T=AA^T$

其中，
$A=U\Lambda^{1/2}$
，因此，通俗地说，

任意一个协方差矩阵都可以视为线性变换的结果

。

在上面的例子中，

特征向量构成的矩阵

为

$U=R=\left[ \begin{array}{cc} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \\ \end{array} \right]=\left[ \begin{array}{cc} \frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \\ \end{array} \right]$
.

特征值构成的矩阵

为

$\Lambda=SS^T=\left[ \begin{array}{cc} s_y^2 & 0 \\ 0 & s_z^2 \\ \end{array} \right]=\left[ \begin{array}{cc} 1 & 0 \\ 0 & \frac{1}{4} \\ \end{array} \right]$
.

到这里，我们发现：多元正态分布的概率密度是由

协方差矩阵的特征向量控制旋转(rotation)

，

特征值控制尺度(scale)

，除了协方差矩阵，

均值向量会控制概率密度的位置

，在图1和图2中，均值向量为
$\boldsymbol{0}$
，因此，概率密度的中心位于坐标原点。

文章结构

1. 方差和协方差的定义

2. 从方差/协方差到协方差矩阵

3. 多元正态分布与线性变换

4. 协方差矩阵的特征值分解

相关参考：

你可能也喜欢