二项式的定义

在数学概念中两个变量的相加，就是二项式。

二项式定理（binomial theorem）主要是讲解二项式整数次幂（或称次方）的代数展开。

$(x+y)^n$
是二项式（x+y）的n次方。

二项式的几何意义

二项式展开与规律性分析

$(x+y)^2=x^2+2xy+y^2$

$(x+y)^3=x^3+3x^2y+3xy^2+y3$

$(x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4$

$(x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5$

从以上可以发现下列规则：

（1）x和y的最高次幂的系数皆是1。

（2）x和y的次高次幂的系数皆是n。

（3）各项
$x^{n-k}y^k$
的指数和为n=n-k+k。

（4）各系数左右对称，由左右两边往中间变大。

Pascal三角形：

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

找出
$x^{n-k}y^k$
项的系数

组合数学（combination）。

$\frac{n!}{(n-k)!k!}=C_{k}^{n}=\binom{n}{r}$

$(x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5$

(1) 验证k=0
$x^5=\frac{5!}{5!0!}=1$

(2) 验证k=1
$x^4y=\frac{5!}{4!1!}=5$

(3) 验证k=2
$x^3y^2=\frac{5!}{3!2!}=10$

(4) 验证k=4
$xy^4=\frac{5!}{1!4!}=5$

(5) 验证k=5
$y^5=\frac{5!}{1!5!}=1$

二项式的通式

$(x+y)^n=\binom{n}{0}x^ny^0+\binom{n}{1}x^{n-1}y^1+\binom{n}{2}x^{n-2}y^2+...+\binom{n}{n-1}x^1y^{n-1}+\binom{n}{n}x^0y^n$

头系数计算是从n中取0个，计算方式如下：
$\binom{n}{0}=\frac{n!}{(n-0)!0!}=\frac{n!}{n!0!}=1$

尾系数计算是从n中取n个，计算方式如下：
$\binom{n}{n}=\frac{n!}{(n-n)!n!}=\frac{n!}{0!n!}=1$

中间系数验证：
$\binom{n}{k}=\binom{n}{n-k}$

二项式到多项式

如果在二项式内增加一个变量z，
$(x+y+z)^2$
，这是三项式。

$(x+y+z)^2=x^2+y^2+z^2+2xy+2yz+2xz$

$\frac{n!}{r1!r2!r3!}$

二项分布实验

成功概率是p，失败概率是1-p

$(p+(1-p))^n$

二项式公式，可以得到p（成功）和(1-p）（失败）出现的次数概率，称二项式分布概率。

将二项式概念应用在业务数据分析

业务员销售第1、2、3、年每拜访客户100次，可以销售国际证照考卷的张数公式，如下所示：

$y=7.5x-3.33$

斜率是7.5，这个斜率意义是每拜访100次，可以销售750张考卷。每拜访10次可以销售7.5张考卷。

每次拜访销售考卷的成功率是0.75。

每5次拜访销售0张考卷的概率

销售失败的概率：
$P(x=0)=1-0.75=0.25$

连续5次拜访皆是失败，概率用公式表示：
$P(x=0)=(0.25)^5$

>>> 0.25**5
0.0009765625
>>>

每5次拜访销售1张考卷的概率

拜访5次可以销售1次的机会：
$\binom{5}{1}$

成功销售1张的概率是0.75，在5次拜访中出现1次，相当于是1次方。

销售失败是4次，失败概率是0.25，相当于是4次方。

$P(x=1)=\binom{5}{1}*0.75^1*(1-0.75)^4$

整个计算结果如下：

>>> 5*0.75*(1-0.75)**4
0.0146484375
>>>

每5次拜访销售2张考卷的概率

拜访5次可以销售2次的机会：
$\binom{5}{2}$

成功销售1张的概率是0.75，在5次拜访中出现2次，相当于是2次方。

销售失败是3次，失败概率是0.25，相当于是3次方。

$P(x=2)=\binom{5}{2}*0.75^2*(1-0.75)^3=10*0.75^2*(1-0.75)^3$

整个计算结果如下：

>>> 10*0.75**2*(1-0.75)**3
0.087890625
>>>

每5次拜访销售0~2张考卷的概率

计算销售0~2张考卷的概率，将上述销售0张、销售1张、销售2张的概率结果相加就可以了。

整个计算结果如下：

>>> 0.0009765625+0.0146484375+0.087890625
0.103515625
>>>

列出拜访5次销售k张考卷的概率通式

拜访5次可以销售k张的机会：
$\binom{5}{k}$

成功销售1张的概率是0.75，在5次拜访中出现k次，是0.75的k次方。

销售失败是5-k次，失败概率是0.25，是0.25的5-k次方。

$P(x=k)=\binom{5}{k}*0.75^k*(1-0.75)^{5-k}$

二项式概率分布Python实践

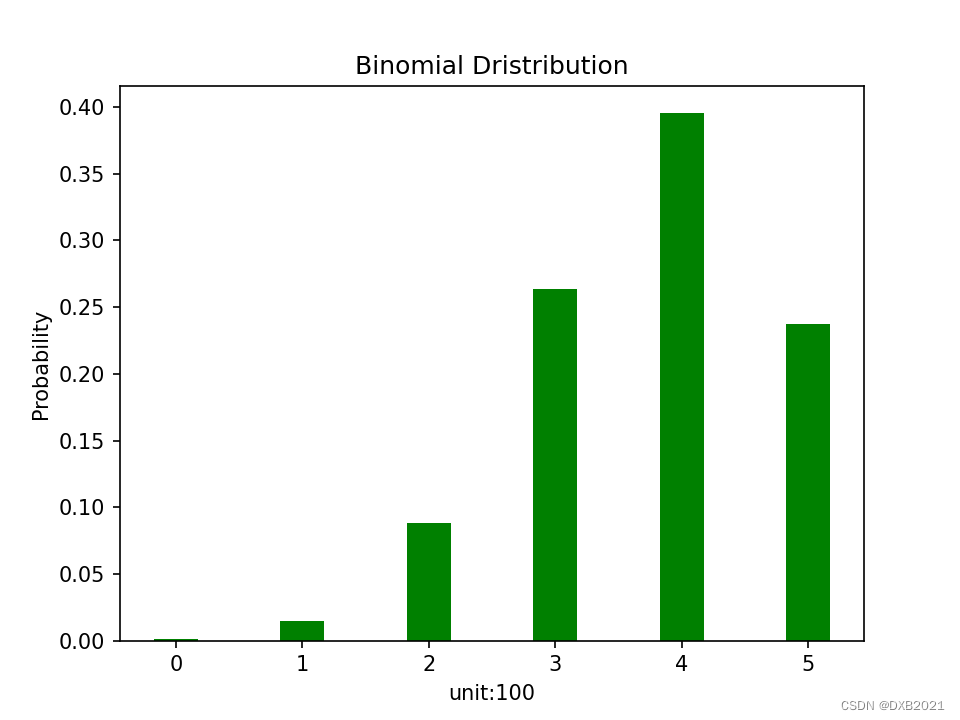
实践销售0~5张考卷的概率，同时使用直方图绘制此图表。

import matplotlib.pyplot as plt
import math 
def probability(k):
    num = (math.factorial(n))/(math.factorial(n-k)*math.factorial(k))
    pro = num * success**k * (1-success)**(n-k)
    return pro
    
n = 5                                           # 销售次数                       # 成功机率
success = 0.75                                  # 销售成功机率
fail = 1 - success                              # 销售失败机率
p = []                                          # 储存成功机率

for k in range(0,n+1):
    if k == 0:
        p.append(fail**n)                       # 连续n次失败机率
        continue
    if k == n:
        p.append(success**n)                    # 连续n次成功机率
        continue
    p.append(probability(k))                    # 计算其他次成功机率

for i in range(len(p)):
    print('销售 {} 单位成功机率 {}%'.format(i, p[i]*100))
        
x = [i for i in range(0, n+1)]                  # 直方图x轴坐标
width = 0.35                                    # 直方图宽度
plt.xticks(x)
plt.bar(x, p, width, color='g')                 # 绘制直方图
plt.ylabel('Probability')
plt.xlabel('unit:100')
plt.title('Binomial Dristribution')
plt.show()

执行结果：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
销售 0 单位成功机率 0.09765625%
销售 1 单位成功机率 1.46484375%
销售 2 单位成功机率 8.7890625%
销售 3 单位成功机率 26.3671875%
销售 4 单位成功机率 39.55078125%
销售 5 单位成功机率 23.73046875%

[Done] exited with code=0 in 11.632 seconds

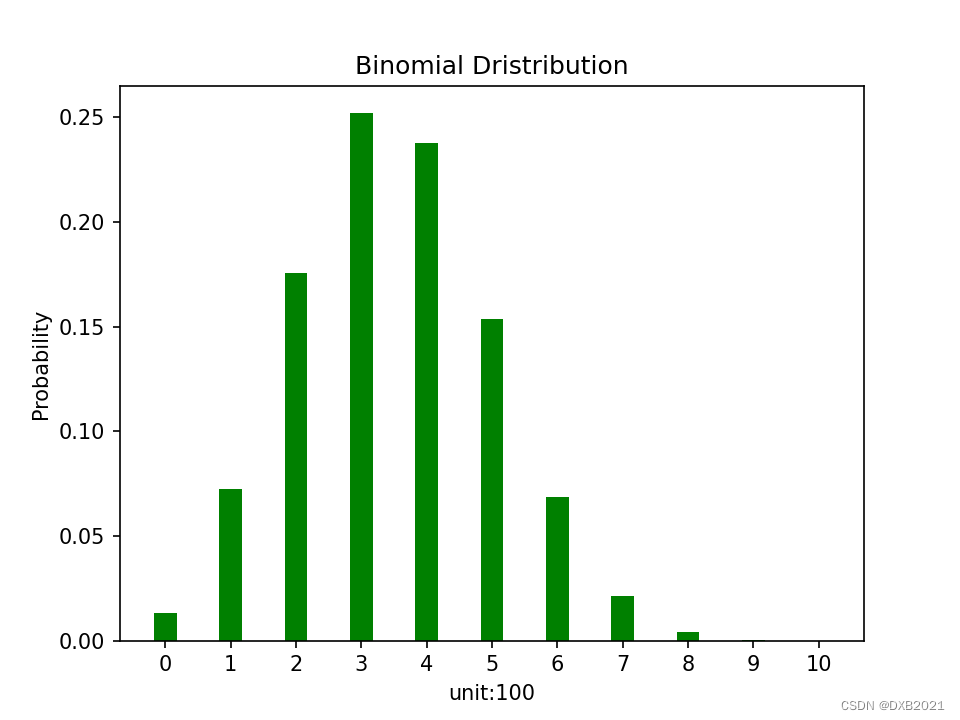
修改成功概率是0.35，然后n是10，计算可能销售0~10张考卷的概率，同时用图表列出结果。

import matplotlib.pyplot as plt
import math 
def probability(k):
    num = (math.factorial(n))/(math.factorial(n-k)*math.factorial(k))
    pro = num * success**k * (1-success)**(n-k)
    return pro
    
n = 10                                          # 销售次数                       # 成功机率
success = 0.35                                  # 销售成功机率
fail = 1 - success                              # 销售失败机率
p = []                                          # 储存成功机率

for k in range(0,n+1):
    if k == 0:
        p.append(fail**n)                       # 连续n次失败机率
        continue
    if k == n:
        p.append(success**n)                    # 连续n次成功机率
        continue
    p.append(probability(k))                    # 计算其他次成功机率

for i in range(len(p)):
    print('销售 {} 单位成功机率 {}%'.format(i, p[i]*100))
        
x = [i for i in range(0, n+1)]                  # 直方图x轴坐标
width = 0.35                                    # 直方图宽度
plt.xticks(x)
plt.bar(x, p, width, color='g')                 # 绘制直方图
plt.ylabel('Probability')
plt.xlabel('unit:100')
plt.title('Binomial Dristribution')
plt.show()

执行结果：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
销售 0 单位成功机率 1.3462743344628911%
销售 1 单位成功机率 7.24916949326172%
销售 2 单位成功机率 17.565295310595708%
销售 3 单位成功机率 25.221962497265626%
销售 4 单位成功机率 23.766849276269532%
销售 5 单位成功机率 15.35704107082031%
销售 6 单位成功机率 6.890979967675779%
销售 7 单位成功机率 2.120301528515624%
销售 8 单位成功机率 0.42813780864257794%
销售 9 单位成功机率 0.05123016513671872%
销售 10 单位成功机率 0.002758547353515623%

[Done] exited with code=0 in 9.087 seconds

原文链接：https://blog.csdn.net/DXB2021/article/details/127168909

二项式的定义

二项式的几何意义

二项式展开与规律性分析

找出 项的系数

二项式的通式

二项式到多项式

二项分布实验

将二项式概念应用在业务数据分析

每5次拜访销售0张考卷的概率

每5次拜访销售1张考卷的概率

每5次拜访销售2张考卷的概率

每5次拜访销售0~2张考卷的概率

列出拜访5次销售k张考卷的概率通式

二项式概率分布Python实践

你可能也喜欢

找出
$x^{n-k}y^k$
项的系数