这是题目:

下面我们开始设计算法:
这是一个最小曼哈顿问题,求解一条最短通路联通图中所有点,使图中任意两点之间是可达的。
下面是算法设计:
(1)采用贪心算法,在已经联通的节点中寻找到任意未联通节点中最短的一条通路,将这个点存入联通节点中,继续下一次循环。通过局部最优解来找到全局最优解。首先任意设定一个起始点,存入联通点集,通过查找起始点和其他所有未联通点集的距离找到最短的那条,并将对应的点存入联通点集。可知每次循环会添加一个联通点,那么遍历整个图只需要九次循环。最后将遍历完成的路径集合和点绘制成图即可。
(2)在已有的图的基础上,采用Djikstra算法,遍历每一个点设置成游客中心的情况,在每一个点成为游客中心的情况下,计算所有点到该游客中心的最短路径,比较这些最短路径,取其中的最大值,作为这个点成为游客中心到最远点的距离。比较十个点都成为游客中心时到各自最远点的距离。找到最短的距离,该距离对应的就是游客中心的位置。
下面是对应的matlab源码:
a=[0,33,51,52,38,61,61,49,53,51;
0,0,44,71,48,51,60,50,49,41;
0,0,0,66,43,58,62,34,35,55;
0,0,0,0,62,56,61,37,49,48;
0,0,0,0,0,55,52,40,28,49;
0,0,0,0,0,0,53,39,49,49;
0,0,0,0,0,0,0,55,50,56;
0,0,0,0,0,0,0,0,64,46;
0,0,0,0,0,0,0,0,0,48;
0,0,0,0,0,0,0,0,0,0];
[row,col]=size(a);
for i=1:row
for p=1:col
a(p,i)=a(i,p);%构建完整的邻接矩阵
end
end
visited=zeros(1,10);
unvisited=[1:10];
visited(1)=1;
unvisited(1)=0;
path=[];
for time=2:10
min=inf;
for m=1:10
p=visited(m);
for n=2:10
q=unvisited(n);
if p~=0&&q~=0&&a(p,q)<min&&a(p,q)~=0
min=a(p,q);%求出局部最优
t=[p,q];
end
end
end
path=[path,t];%将该路径存入path
visited(time)=t(2);
for b=1:10
if unvisited(b)==t(2)
unvisited(b)=0;
end
end
end
weights=[];
distance=0;
for h=1:2:18
weights=[weights,a(path(h),path(h+1))];
distance=distance+a(path(h),path(h+1));
end
path
distance
得到了相应的path数组如下:path =
1 2 1 5 5 9 9 3 3 8 8 4 8 6 2 10 9 7
distance =
335
在此基础上我们解决第二问
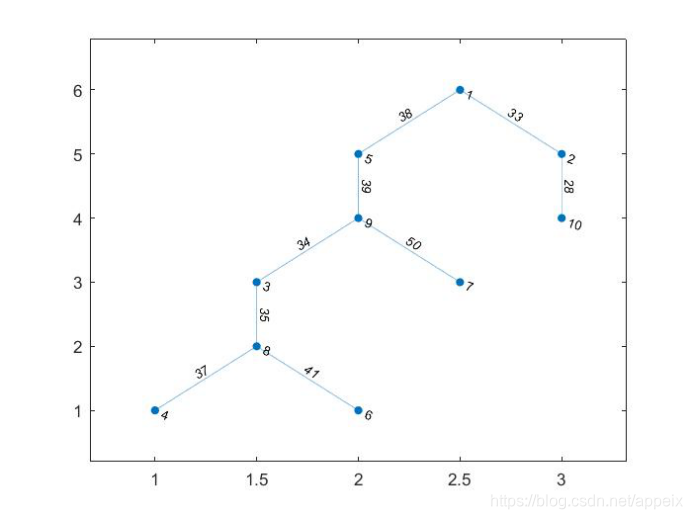
我们可以根据结果手动创建一个图(当然也可以编程实现,但是这还是会涉及到一些算法)
s=[1,1,2,3,3,4,5,6,7];
t=[2,5,10,8,9,8,9,8,9];
G= graph(s,t,weights);
plot(G,'EdgeLabel',G.Edges.Weight)
max=zeros(1,10);
for u=1:10
for v=1:10
[t,d]=shortestpath(G,u,v);%依次寻找每个节点到其余所有节点的最短路径
if d>max(u)
max(u)=d;%找到这些最短路径中最长的
end
end
end
max %这个数组代表了10个节点中,每个节点建游客中心时到该游中
%心最远节点的距离找出这些值中的最小值
得到了对应的连通图:
然后我们得到了max数组:max =
187 220 172 244 149 248 188 207 138 248
问题解决