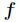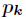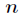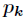前言: 通过拉格朗日乘数法可以将原来带约束的优化问题转换为无约束的优化问题。
拉格朗日乘数法(Lagrange Multiplier Method)之前听数学老师授课的时候就是一知半解,现在越发感觉拉格朗日乘数法应用的广泛性,所以特意抽时间学习了麻省理工学院的在线数学课程。新学到的知识一定要立刻记录下来,希望对各位博友有些许帮助。
1. 拉格朗日乘数法的基本思想
作为一种优化算法,拉格朗日乘子法主要用于解决约束优化问题,它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
如何将一个
含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题?拉格朗日乘数法从数学意义入手,通过引入拉格朗日乘子建立极值条件,对n个变量分别求偏导对应了n个方程,然后加上k个约束条件(对应k个拉格朗日乘子)一起构成包含了(n+k)变量的(n+k)个方程的方程组问题,这样就能根据求方程组的方法对其进行求解。
解决的问题模型为约束优化问题:
min/max a function f(x,y,z), where x,y,z are not independent and g(x,y,z)=0.
即:min/max f(x,y,z)
s.t. g(x,y,z)=0
2. 数学实例
首先,我们先以麻省理工学院数学课程的一个实例来作为介绍拉格朗日乘数法的引子。
【麻省理工学院数学课程实例】求双曲线xy=3上离远点最近的点。
解:
首先,我们根据问题的描述来提炼出问题对应的数学模型,即:
min f(x,y)=x
2
+y
2
(两点之间的欧氏距离应该还要进行开方,但是这并不影响最终的结果,所以进行了简化,去掉了平方)
s.t. xy=3.
根据上式我们可以知道这是一个典型的约束优化问题,其实我们在解这个问题时最简单的解法就是通过约束条件将其中的一个变量用另外一个变量进行替换,然后代入优化的函数就可以求出极值。我们在这里为了引出拉格朗日乘数法,所以我们采用拉格朗日乘数法的思想进行求解。
我们将x
2
+y
2
=c的曲线族画出来,如下图所示,当曲线族中的圆与xy=3曲线进行相切时,切点到原点的距离最短。也就是说,当f(x,y)=c的等高线和双曲线g(x,y)相切时,我们可以得到上述优化问题的一个极值(注意:如果不进一步计算,在这里我们并不知道是极大值还是极小值)。

现在原问题可以转化为求当f(x,y)和g(x,y)相切时,x,y的值是多少?
如果两个曲线相切,那么它们的切线相同,即法向量是相互平行的,▽f//▽g.
由▽f//▽g可以得到,▽f=λ*▽g。
这时,我们将原有的约束优化问题转化为了一种对偶的无约束的优化问题,如下所示:
原问题:
min f(x,y)=x
2
+y
2
对偶问题:
由▽f=λ*▽g得,
s.t. xy=3 f
x
=λ*g
x,
f
y
=λ*g
y,
xy=3.
约束优化问题 无约束方程组问题
通过求解右边的方程组我们可以获取原问题的解,即
2x=λ*y
2y=λ*x
xy=3
通过求解上式可得,λ=2或者是-2;当λ=2时,(x,y)=(sqrt(3), sqrt(3))或者(-sqrt(3), -sqrt(3)),而当λ=-2时,无解。所以原问题的解为(x,y)=(sqrt(3), sqrt(3))或者(-sqrt(3), -sqrt(3))。
通过举上述这个简单的例子就是为了体会拉格朗日乘数法的思想,即通过引入拉格朗日乘子(λ)将原来的约束优化问题转化为无约束的方程组问题。
3. 拉格朗日乘数法的基本形态
求函数
![]()
在满足
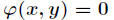
下的条件极值,可以转化为函数

的无条件极值问题。
我们可以画图来辅助思考。

绿线标出的是约束g(x,y)=c的点的轨迹。蓝线是f(x,y)的等高线。箭头表示斜率,和等高线的法线平行。
从图上可以直观地看到在最优解处,f和g的斜率平行。
▽[f(x,y)+λ(g(x,y)−1)]=0, λ≠0
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
F(x,y)=f(x,y)+λ(g(x,y)−c)
新方程F(x,y)在达到极值时与f(x,y)相等,因为F(x,y)达到极值时g(x,y)−c总等于零。
上述式子取得极小值时其导数为0,即▽f(x)+▽∑λ
i
g
i
(x)=0,也就是说f(x)和g(x)的梯度共线。
题目1:
给定椭球

求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题,即在条件
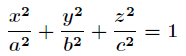
下,求

的最大值。
当然这个问题实际可以先根据条件消去

,然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用
拉格朗日乘数法
了。通过拉格朗日乘数法将问题转化为

对

求偏导得到

联立前面三个方程得到

和
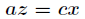
,带入第四个方程解之

带入解得最大体积为

拉格朗日乘数法对一般多元函数在多个附加条件下的条件极值问题也适用。
题目2:
题目:
求离散分布的最大熵。
分析:
因为离散分布的熵表示如下
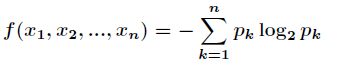
而约束条件为
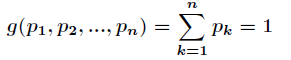
要求函数
的最大值,根据
拉格朗日乘数法
,设
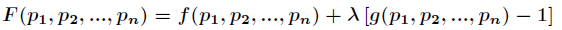
对所有的
求偏导数,得到
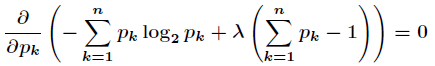
计算出这
个等式的微分,得到
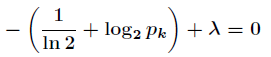
这说明所有的
都相等,最终解得
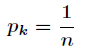
因此,使用
均匀分布
可得到最大熵的值。
4. 拉格朗日乘数法与KKT条件
我们上述讨论的问题均为等式约束优化问题,但等式约束并不足以描述人们面临的问题,不等式约束比等式约束更为常见,大部分实际问题的约束都是不超过多少时间,不超过多少人力,不超过多少成本等等。所以有几个科学家拓展了拉格朗日乘数法,增加了KKT条件之后便可以用拉格朗日乘数法来求解不等式约束的优化问题了。
首先,我们先介绍一下什么是KKT条件。
KKT条件是指在满足一些有规则的条件下, 一个非线性规划(Nonlinear Programming)问题能有最优化解法的一个必要和充分条件.
这是一个广义化拉格朗日乘数的成果. 一般地, 一个最优化数学模型的列标准形式参考开头的式子, 所谓 Karush-Kuhn-Tucker 最优化条件,就是指上式的最优点x
∗
必须满足下面的条件:
1). 约束条件满足g
i
(x
∗
)≤0,i=1,2,…,p, 以及,hj(x
∗
)=0,j=1,2,…,q
2). ∇f(x
∗
)+∑
i=1
μ
i
∇g
i
(x
∗
)+∑
j=1
λ
j
∇h
j
(x
∗
)=0, 其中∇为梯度算子;
3). λ
j
≠0且不等式约束条件满足μ
i
≥0,μ
i
g
i
(x
∗
)=0,i=1,2,…,p。
KKT条件第一项是说最优点x
∗
必须满足所有等式及不等式限制条件, 也就是说最优点必须是一个可行解, 这一点自然是毋庸置疑的. 第二项表明在最优点x
∗
, ∇f必须是∇g
i
和∇h
j
的线性組合, μ
i
和λ
j
都叫作拉格朗日乘子. 所不同的是不等式限制条件有方向性, 所以每一个μ
i
都必须大于或等于零, 而等式限制条件没有方向性,所以λ
j
没有符号的限制, 其符号要视等式限制条件的写法而定.
为了更容易理解,我们先举一个例子来说明一下KKT条件的由来。
l
e
t
L
(
x
,
μ
)
=
f
(
x
)
+
∑
k
=
1
μ
k
g
k
(
x
),
其中μ
k
≥0,g
k
(x)≤0
∵μ
k
≥0 g
k
(x)≤0 => μ
g
(x)≤0
∴max
μ
L(x,μ)=f(x) (2)
∴min
x
f(x)=min
x
max
μ
L(x,μ) (3)
max
μ
min
x
L
(
x
,
μ
)
=
max
μ
[
min
x
f
(
x
)
+
min
x
μ
g
(
x
)
]
=
max
μ
min
x
f
(
x
)
+
max
μ
min
x
μ
g
(
x
)
=
min
x
f
(
x
)
+
max
μ
min
x
μ
g
(
x
)
又
∵μ
k
≥0, g
k
(x)≤0
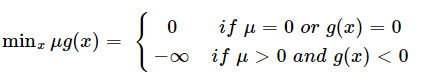
∴max
μ
min
x
μg(x)=0, 此时μ=0 or g(x)=0.
∴
max
μ
min
x
L
(
x
,
μ
)
=
min
x
f
(
x
)
+
max
μ
min
x
μ
g
(
x
)
=
min
x
f
(
x
)
(4)
此时
μ
=
0
o
r
g
(
x
)
=
0.
x
max
μ
L(x,μ)=max
μ
min
x
L(x,μ), 亦即

min
x
max
μ
L(x,μ)=max
μ
min
x
L(x,μ)=min
x
f(x)
我们把max
μ
min
x
L(x,μ)称为原问题min
x
max
μ
L(x,μ)的对偶问题,上式表明当满足一定条件时原问题、对偶的解、以及min
x
f(x)是相同的,且在最优解x
∗
处μ=0 or g(x
∗
)=0。把x
∗
代入(2)得max
μ
L(x
∗
,μ)=f(x
∗
),由(4)得max
μ
min
x
L(x,μ)=f(x
∗
),所以L(x
∗
,μ)=min
x
L(x,μ),这说明x
∗
也是L(x,μ)的极值点,即
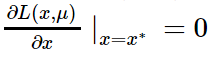
最后总结一下:

KKT条件是拉格朗日乘子法的泛化,如果我们把等式约束和不等式约束一并纳入进来则表现为:
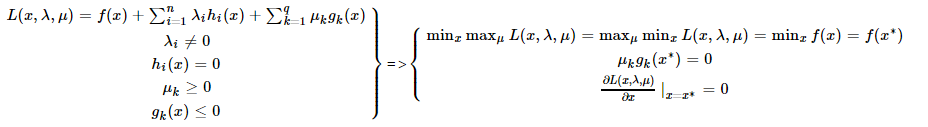
注:x,λ,μ都是向量。
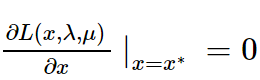
表明f(x)在极值点x
∗
处的梯度是各个h
i
(x
∗
)和g
k
(x
∗
)梯度的线性组合。
其他参考资料
简易解说拉格朗日对偶
拉格朗日对偶