大家好,我是哪吒,一个热爱编码的Java工程师,本着“欲速则不达,欲达则欲速”的学习态度,在程序猿这条不归路上不断成长,所谓成长,不过是用时间慢慢擦亮你的眼睛,少时看重的,年长后却视若鸿毛,少时看轻的,年长后却视若泰山,成长之路,亦是渐渐放下执念,内心归于平静的旅程。
也许,我们永远都不会知道自己能走到何方,遇见何人,最后会变成什么样的人,但一定要记住,能让自己登高的,永远不是别人的肩膀,而是挑灯夜战的自己,人生的道路刚刚启程,当你累了倦了也不要迷茫,回头看一看,你早已不再是那个年少轻狂的少年。
目录
2、将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再讲堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
3、重新调整结构,使其继续满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
一、前言
数组的搜索比较方便,可以直接用下标,但删除和插入就比较麻烦;
链表与之相反,删除和插入元素很快,但查找比较慢;
此时,二叉树应运而生,二叉树既有链表的好处,也有数组的好处,在处理大批量的动态数据时比较好用,是一种折中的选择。
文件系统和数据库系统一般都是采用树(特别是B树)的数据结构数据,主要为排序和检索的效率。
二叉树是一种最基本最典型的排序树,用于教学和研究树的特性,本身很少在实际中进行应用,因为缺点太明显,就像冒泡排序一样,因为效率问题并不实用,但也是我们必须会的。
二、二叉树缺点
1、顺序存储可能会浪费空间(在非完全二叉树的时候),但是读取某个指定的结点的时候效率比较高O(0);
2、链式存储相对于二叉树,浪费空间较少,但是读取某个结点的时候效率偏低O(nlogn)。
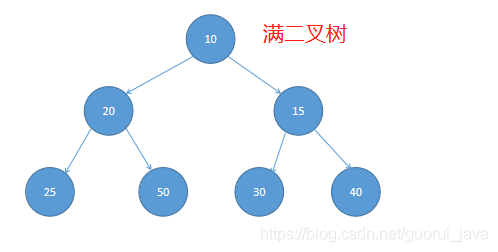
满二叉树:
在一颗二叉树中,如果所有分支结点都有左子结点和右子结点,并且叶结点都集中在二叉树的最底层,这样的二叉树称为满二叉树。
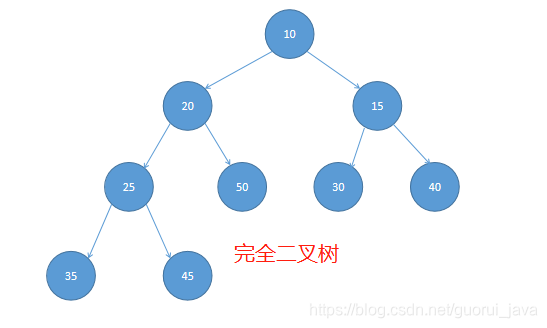
完全二叉树:
若二叉树中最多只有最下面两层的结点,而且相差只有1级,并且最下面一层的叶结点都依次排列在该层的最左边位置,则这样的二叉树称为完全二叉树。
三、遍历与结点删除
二叉树是一种非常重要的数据结构,非常多的数据结构都是基于二叉树的基础演变而来的。对于二叉树有深度遍历和广度遍历,深度遍历有前序、中序以及后序三种遍历方法,广度遍历即我们寻常所说的层次遍历。由于树的定义本身就是递归定义,因此采用递归的方法实现树的三种遍历。
对于一段代码来说,可读性有时候要比代码本身的效率要重要的多。
1、四种基本的遍历思想
- 前序遍历:根结点 –>左子树–>右子树;
- 中序遍历:左子树 –>根结点–>右子树;
- 后续遍历:左子树 –>右子树–>根结点;
- 层次遍历:仅仅需按成次遍历即可;
2、自定义二叉树
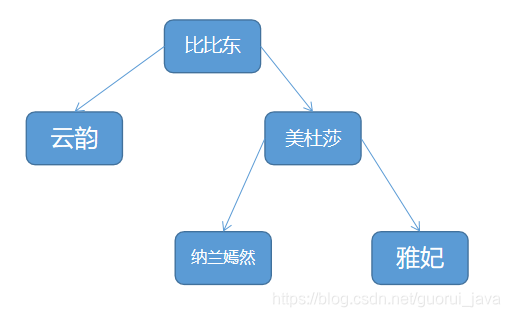
3、代码实现
(1)girlNode
package com.guor.tree;
public class GirlNode {
private int no;
private String name;
private GirlNode left; //默认null
private GirlNode right; //默认null
//1、如果leftType == 0表示指向的是左子树,如果 leftType == 1则表示指向的是前驱结点
//2、如果rightType == 0表示指向的是右子树,如果 rightType == 1则表示指向的是后继结点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public GirlNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public GirlNode getLeft() {
return left;
}
public void setLeft(GirlNode left) {
this.left = left;
}
public GirlNode getRight() {
return right;
}
public void setRight(GirlNode right) {
this.right = right;
}
@Override
public String toString() {
return "GirlNode [no=" + no + ", name=" + name + "]";
}
//前序遍历
public void preOrder() {
System.out.println(this);//先输出父节点
//递归向左子树前序遍历
if(this.left != null) {
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.preOrder();
}
}
//中序遍历
public void midOrder() {
//递归向左子树中序遍历
if(this.left != null) {
this.left.midOrder();
}
System.out.println(this);//输出父节点
//递归向右子树前序遍历
if(this.right != null) {
this.right.midOrder();
}
}
//后序遍历
public void postOrder() {
//递归向左子树后序遍历
if(this.left != null) {
this.left.postOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);//输出父节点
}
//递归删除结点
//1.如果删除的节点是叶子节点,则删除该节点
//2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) {
//思路
/*
* 1. 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点.
2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
3. 如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
4. 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
5. 如果第4步也没有删除结点,则应当向右子树进行递归删除.
*/
//2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4.我们就需要向左子树进行递归删除
if(this.left != null) {
this.left.delNode(no);
}
//5.则应当向右子树进行递归删除
if(this.right != null) {
this.right.delNode(no);
}
}
}
(2)二叉树测试
package com.guor.tree;
public class BinaryTreeTest {
public static void main(String[] args) {
//创建一个二叉树
BinaryTree binaryTree = new BinaryTree();
//创建结点
HeroNode root = new HeroNode(1, "比比东");
HeroNode node2 = new HeroNode(2, "云韵");
HeroNode node3 = new HeroNode(3, "美杜莎");
HeroNode node4 = new HeroNode(4, "纳兰嫣然");
HeroNode node5 = new HeroNode(5, "雅妃");
root.setLeft(node2);
root.setRight(node3);
node3.setLeft(node4);
node3.setRight(node5);
binaryTree.setRoot(root);
System.out.println("前序遍历");
binaryTree.preOrder();
System.out.println("中序遍历");
binaryTree.midOrder();
System.out.println("后序遍历");
binaryTree.postOrder();
binaryTree.delNode(3);
System.out.println("删除结点3,前序遍历");
binaryTree.preOrder();
}
}
//定义BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public HeroNode getRoot() {
return root;
}
public void setRoot(HeroNode root) {
this.root = root;
}
//前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,不能遍历");
}
}
//中序遍历
public void midOrder() {
if(this.root != null) {
this.root.midOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//删除结点
public void delNode(int no) {
if(root != null) {
//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if(root.getNo() == no) {
root = null;
} else {
//递归删除
root.delNode(no);
}
}else{
System.out.println("空树,不能删除~");
}
}
}
(3)控制台输出
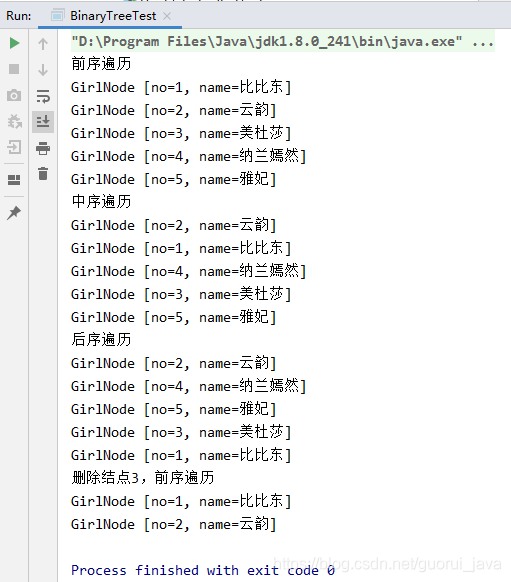
四、先看一个问题
将数列{1,3,6,8,10,14}构建成一颗二叉树。
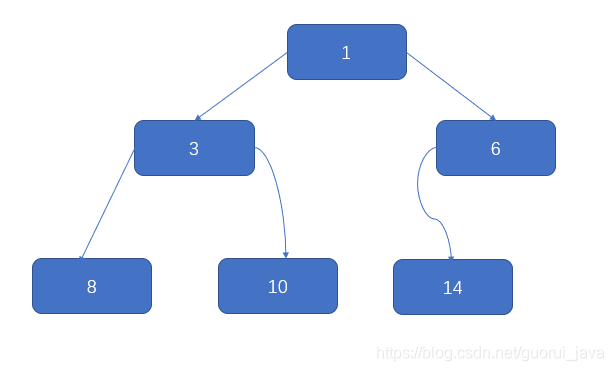
问题分析:
- 当我们对上面的二叉树进行中序遍历时,数列为{8,3,10,1,6,14}。
- 但是6,8,10,14这几个节点的左右指针,并没有完全的利用上。
- 如果我们希望充分的利用各个节点的左右指针,让各个节点可以指向自己的前后节点,要怎么办?
- 解决方案 –> 线索化二叉树
五、线索化二叉树
1、n个节点的二叉树链表总含有n+1(公式2n-(n-1)=n+1)个空指针域。利用二叉树表中的空指针域,存放指向该节点在某种遍历次序下的前驱和后继节点的指针(这种附加的指针称为“线索”)
2、这种加上了线索的二叉树称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
3、一个节点的前一个节点,称为前驱节点
4、一个节点的后一个节点,称为后继节点
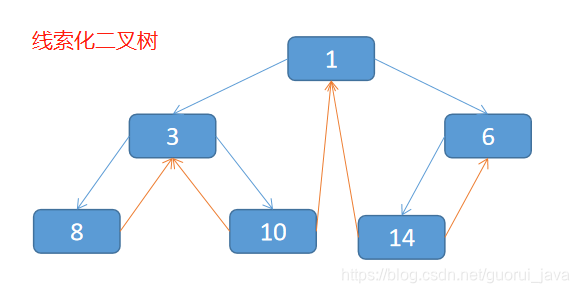
说明:当线索化二叉树后,Node节点的属性left和right,有如下情况:
- left指向的是左子树,也可能指向的前驱节点,比如①节点left指向的左子树,而⑩节点的left指向的就是前驱节点。
- right指向的是右子树,也可能是指向后继节点,比如①节点right指向的是右子树,而⑩节点的right指向的是后继节点。
六、线索化二叉树代码实例
1、线索化二叉树
package com.guor.tree;
//定义ThreadBinaryTree,实现了线索化功能的二叉树
public class ThreadedBinaryTree {
private HeroNode root;
//为了实现线索化,需要创建指向当前结点的前驱结点的指针
//在递归进行线索化时,pre总是保留前一个结点
private HeroNode pre = null;
public HeroNode getRoot() {
return root;
}
public void setRoot(HeroNode root) {
this.root = root;
}
//重载threadedNodes方法
public void threadedNodes(){
this.threadedNodes(root);
}
/**
* 编写对二叉树进行中序线索化的方法
* @param node 当前需要线索化的结点
*/
public void threadedNodes(HeroNode node){
//如果node==null,不能线索化
if(node == null){
return;
}
//1、先线索化左子树
threadedNodes(node.getLeft());
//2、线索化当前结点
//处理当前结点的前驱结点
//以8为例来理解
//8结点的.left = null,8结点的.leftType = 1
if(node.getLeft() == null){
//让当前结点的左指针指向前驱结点
node.setLeft(pre);
//修改当前结点的左指针的类型,指向前驱结点
node.setLeftType(1);
}
//处理后继结点
if(pre != null && pre.getRight() == null){
//让当前结点的右指针指向当前结点
pre.setRight(node);
//修改当前结点的右指针的类型=
pre.setRightType(1);
}
//每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
//3、线索化右子树
threadedNodes(node.getRight());
}
//前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,不能遍历");
}
}
//中序遍历
public void midOrder() {
if(this.root != null) {
this.root.midOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//删除结点
public void delNode(int no) {
if(root != null) {
//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if(root.getNo() == no) {
root = null;
} else {
//递归删除
root.delNode(no);
}
}else{
System.out.println("空树,不能删除~");
}
}
}
2、测试
package com.guor.tree;
public class ThreadedBinaryTreeTest {
public static void main(String[] args) {
//测试中序线索二叉树的功能
HeroNode root = new HeroNode(1,"比比东");
HeroNode node2 = new HeroNode(3,"云韵");
HeroNode node3 = new HeroNode(6,"纳兰嫣然");
HeroNode node4 = new HeroNode(8,"雅妃");
HeroNode node5 = new HeroNode(10,"千仞雪");
HeroNode node6 = new HeroNode(14,"美杜莎");
//二叉树,后面我们要递归创建,现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
//测试中序线索化
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
threadedBinaryTree.threadedNodes();
//以10号节点测试
HeroNode leftNode = node5.getLeft();
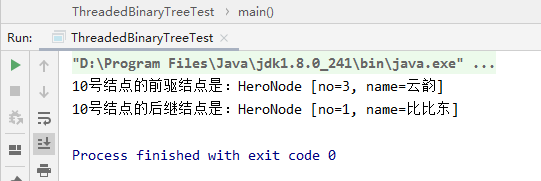
System.out.println("10号结点的前驱结点是:"+leftNode);//应该是3号
HeroNode rightNode = node5.getRight();
System.out.println("10号结点的后继结点是:"+rightNode);//应该是1号
}
}
3、控制台输出
七、遍历线索化二叉树
说明:对前面的中序线索化的二叉树,进行遍历
分析:因为线索化后,各个结点指向有变化,因此原来的遍历方式不能使用,这时需要使用心得方式遍历线索化二叉树,各个结点可以通过线型方式遍历,因此无需使用递归方式,这样也提高了遍历的效率。遍历的次序应当和中序遍历保持一致。
1、代码实例
/**
* 遍历线索化二叉树的方法
*/
public void threadedList(){
//定义一个变量,存储当前遍历的结点,从root开始
HeroNode node = root;
while (node != null){
//循环找到leftType == 1的结点,第一个找到就是8结点
//后面随着遍历而变化,因为当leftType==1时,说明该结点是按照线索化处理后的有效结点
while(node.getLeftType() == 0){
node = node.getLeft();
}
//打印当前结点
System.out.println(node);
//如果当前结点的右指针指向的是后继结点,就一直输出
while(node.getRightType() == 1){
//获取当前结点的后继结点
node = node.getRight();
System.out.println(node);
}
//替换这个遍历的结点
node = node.getRight();
}
}
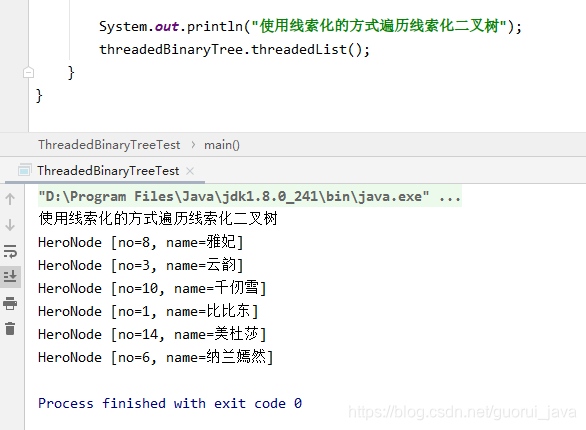
2、控制台输出
八、大顶堆和小顶堆图解说明
1、堆排序基本介绍
-
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为
线性对数阶
,它也是不稳定排序。 - 堆是具有以下特性的完全二叉树:每个结点的值都大于或等于其左右子结点的值,称为大顶堆,注意:没有要求结点的左子结点值和右子结点值的大小关系。
- 每个结点的值都小于或等于其左右子结点的值,称为小顶堆。
2、大顶堆举例说明
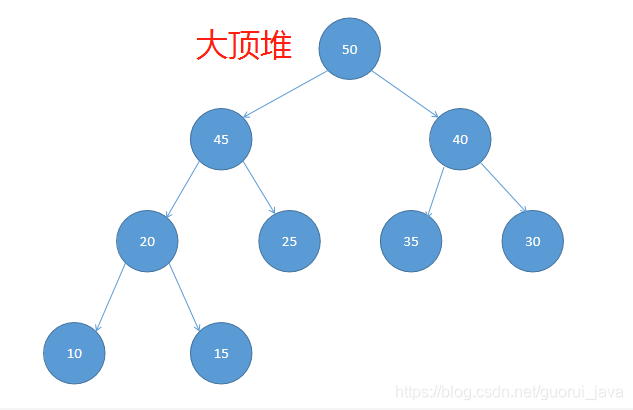
我们对堆中的结点按层进行编号,映射到数组中就是下面这一个样子
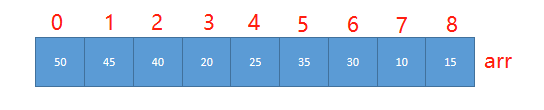
大顶堆特点:
arr[i]>=ar[2*i+1]&&arr[i]>=arr[2*i+2]//i对应第几个结点,i从0开始编号
3、小顶堆距离说明
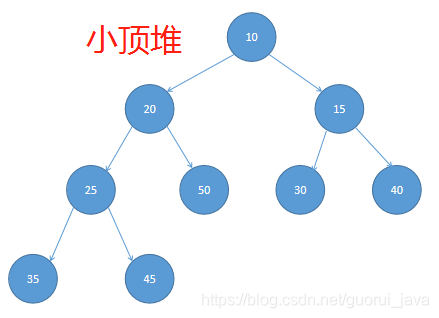
小顶堆特点:
arr[i]<=arr[2*i+1]&&arr[i]<=arr[2*i+2]//i对应第几个结点,i从0开始编号
4、一般升序采用大顶堆,降序采用小顶堆
九、堆排序基本思想
- 将待排序序列构成一个大顶堆
- 此时,整个序列的最大值就是堆顶的根节点
- 将其与末尾元素进行交换,此时末尾就为最大值
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
九、堆排序思路和步骤解析
1、将无序二叉树调整为大顶堆
(1)原始的数组[4,6,8,5,9]
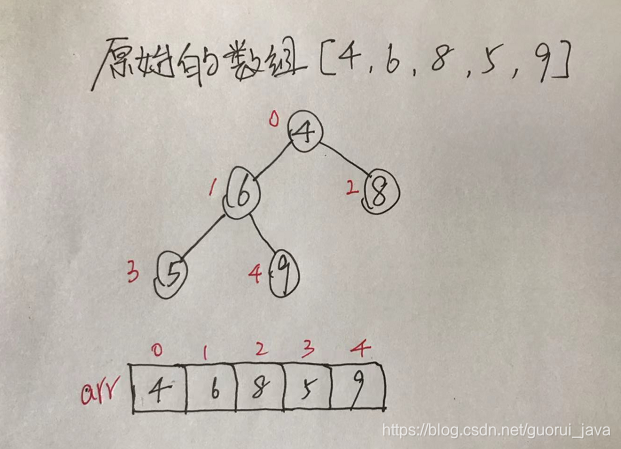
(2)此时从最后一个非叶子结点开始(第一个非叶子结点arr.length/2-1=5/2-1=1,也就是6结点),从左至右,从上至下进行调整。
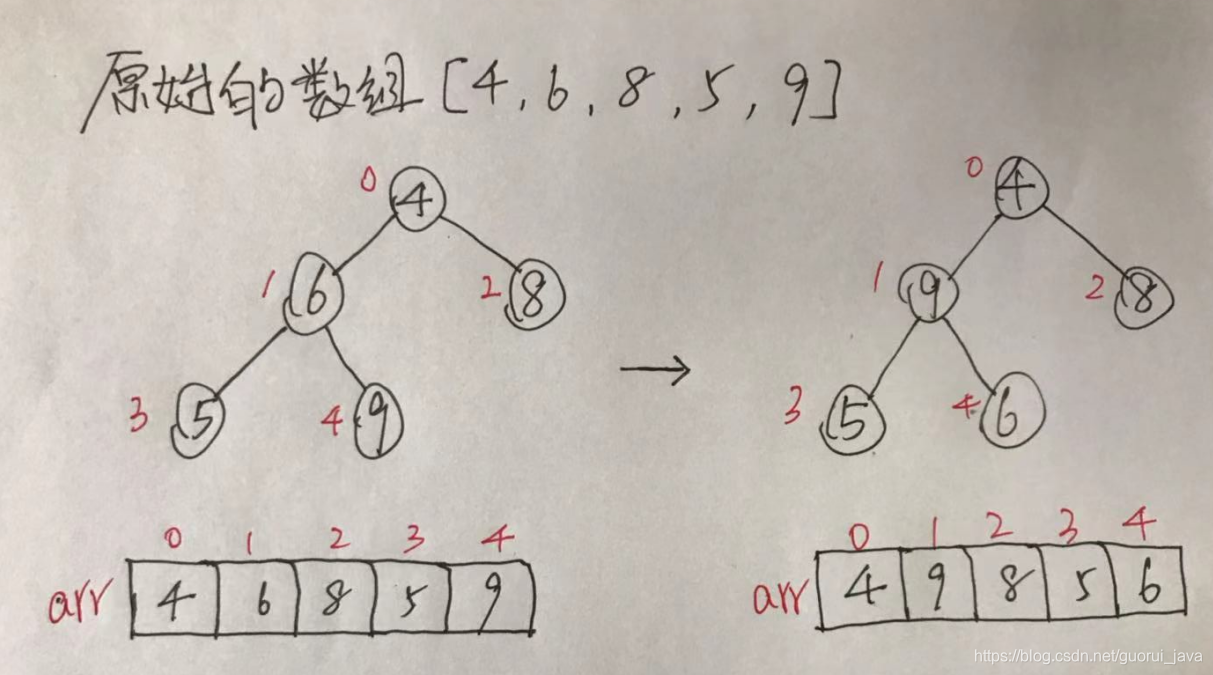
(3)再找到第二个非叶子结点,由于[4,9,8]中9最大,所以4和9交换。
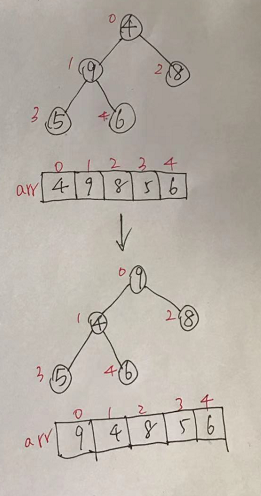
4、此时,交换之后导致[4,5,6]结构混乱了,继续调整,交换4和6。
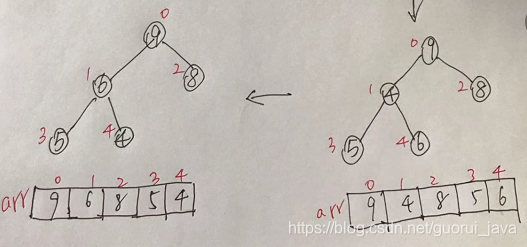
此时,我们就讲一个无序结构的二叉树调整为了一个大顶堆。
2、将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再讲堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
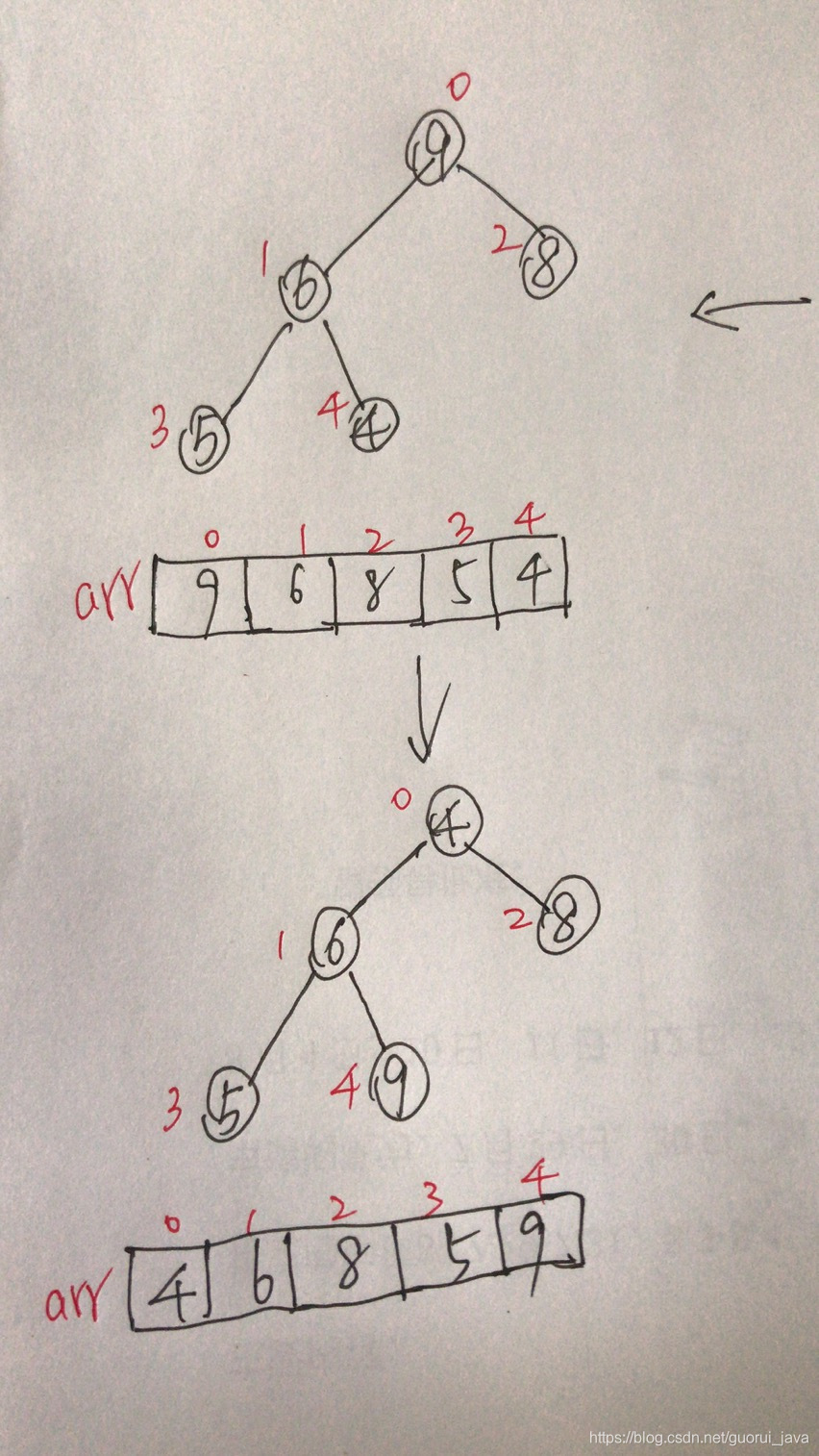
3、重新调整结构,使其继续满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
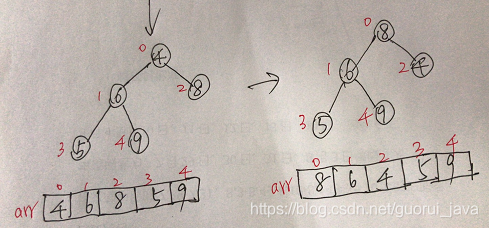
再将堆顶的8与末尾元素5交换,得到第二大元素8
然后继续进行调整,交换,最后变成:
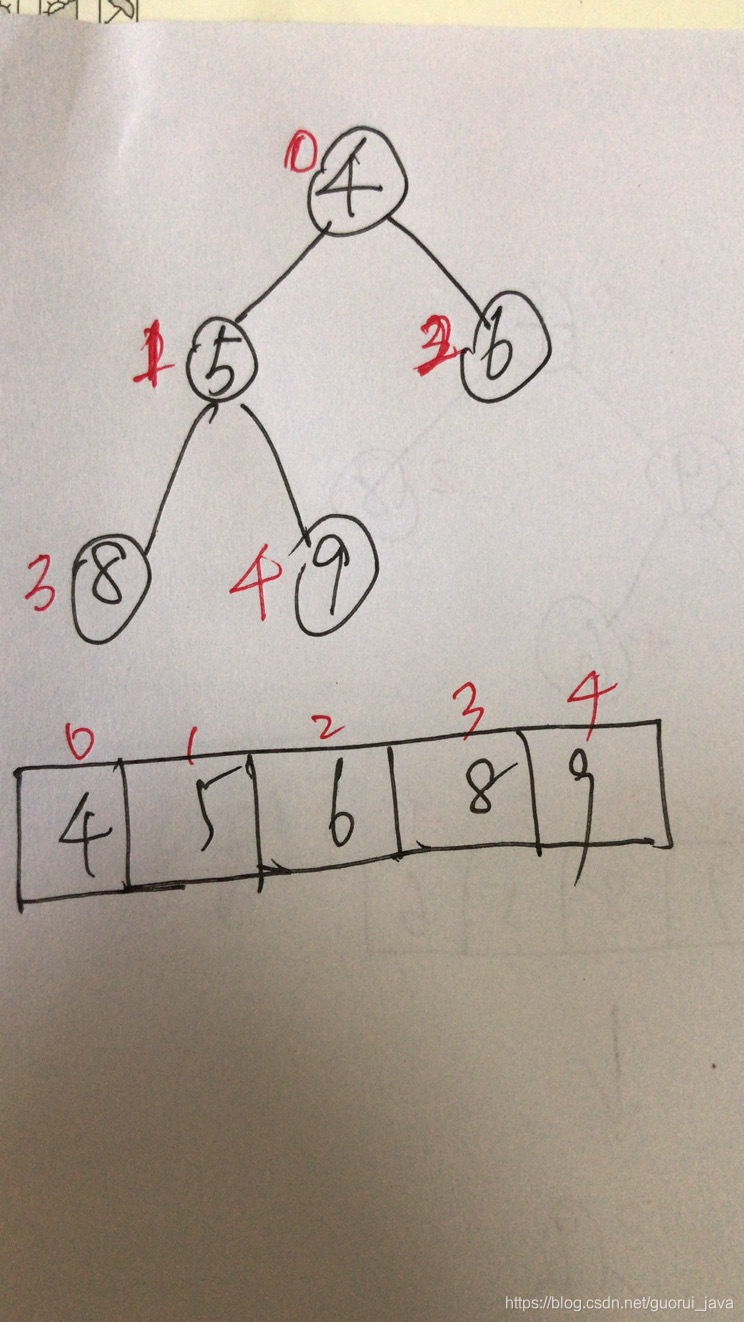
简单总结一下堆排序的基本思路:
- 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素交换至数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
十、堆排序代码实例
1、堆排序代码
package com.guor.tree;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
//要求将数组进行升序排序
int arr[] = {4,6,8,5,9};
heapSort(arr);
}
public static void heapSort(int arr[]){
int temp = 0;
System.out.println("堆排序。");
//分步完成
//adjustHeap(arr,1,arr.length);
//System.out.println("第一次调整:"+ Arrays.toString(arr));//{4,9,8,5,6}
//adjustHeap(arr,0,arr.length);
//System.out.println("第二次调整:"+ Arrays.toString(arr));//{9,6,8,5,4}
//完成最终代码
//将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
//arr.length/2-1为叶子结点个数
for(int i = arr.length/2-1;i>=0;i--){
adjustHeap(arr, i, arr.length);
}
System.out.println("调整为大顶堆:"+ Arrays.toString(arr));//大顶堆{9,6,8,5,4}
//第二步:将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再讲堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
//第三步:重新调整结构,使其继续满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
for(int j = arr.length - 1;j > 0; j--){
//交换
temp=arr[j];
arr[j]= arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
System.out.println("最终有序序列:"+ Arrays.toString(arr));//大顶堆{4,5,6,8,9}
}
/**
* 功能:完成将以i为叶子节点的树调整为大顶堆
* @demo int arr[] = {4,6,8,5,9};i = 1 --> adjustHeap --> {4,9,8,5,6}
* 如果再调用adjustHeap,传入i=0 --> 大顶堆{9,6,8,5,4}
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中的索引
* @param length 表示对多少个元素进行继续调整,length逐渐减少
*/
public static void adjustHeap(int arr[], int i, int length){
//取出当前元素的值,保存为临时变量
int temp = arr[i];
//1、k = i * 2 + 1 ,k是i结点的左子结点
for(int k = i * 2 + 1; k < length; k = k * 2 + 1){
//左子结点的值小于右子结点的值
if(k+1<length && arr[k] < arr[k+1]){
k++;//k指向右子结点
}
//如果子结点大于父节点
if(arr[k] > temp){
arr[i] = arr[k];//将较大的值赋给当前结点
i = k;//i指向k,继续循环比较
}else{
break;
}
}
//当for循环结束后,我们已经将以i为父节点的树的最大值,放在了最顶,完成局部大顶堆
arr[i] = temp;//将temp值放到调整后的位置
}
}
2、堆排序控制台输出
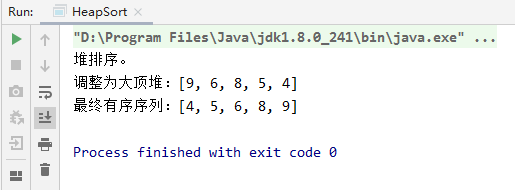
3、堆排序性能测试
因为堆排序的时间复杂度是线性对数阶,所以堆排序是非常快的,性能相当强悍,拿1000万条数据进行排序测试一下,let‘s go!
public static void main(String[] args) {
//模拟测试1000万条数据
int[] arr = new int[10000000];
for(int i = 0; i< 10000000; i++){
arr[i] = (int)(Math.random() * 10000000);
}
long start = new Date().getTime();
heapSort(arr);
long end = new Date().getTime();
System.out.println("1000万条数据,堆排序耗时:"+(end-start)+"ms");
}
4、性能测试控制台输出
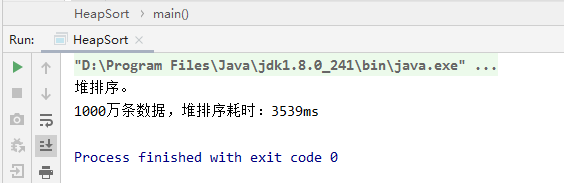
十一、赫夫曼树
1、基本介绍
(1)给定n个权值作为n个叶子结点,构造一颗二叉树,若该树的带权路径长度wpl达到最小,称这样的二叉树为最优二叉树,也称为赫夫曼树。
(2)赫夫曼树是带权路径长度最短的树,权重较大的结点离根较近。
2、赫夫曼树几个重要概念和举例说明
(1)路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
(2)结点的权及带权路径长度
若将树中结点赋给一个有着某种意义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
(3)树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,为WPL(weighted path length),权重越大的结点离根结点越近的二叉树才是最优二叉树。
(4)WPL最小的就是赫夫曼树。
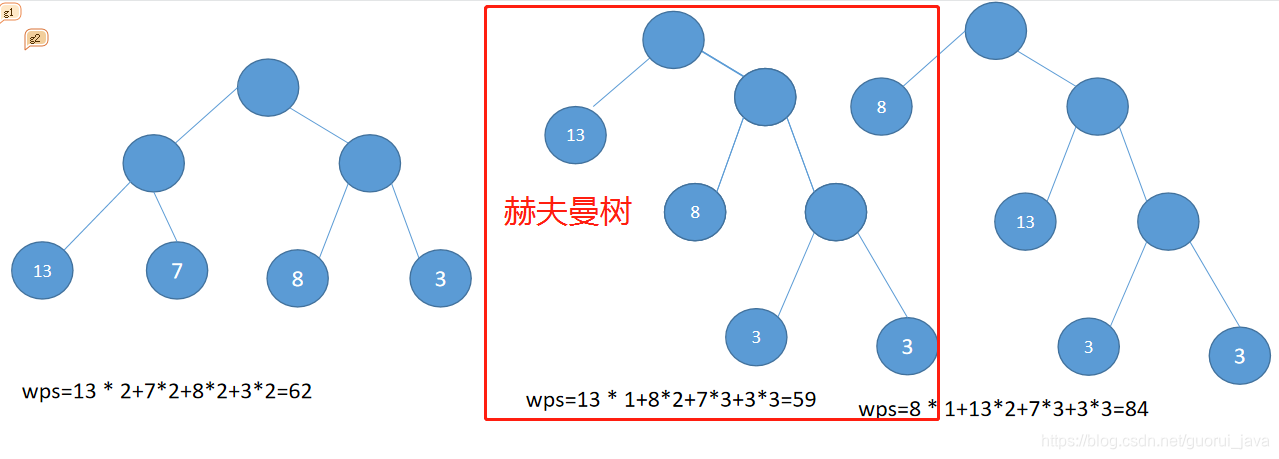
3、赫夫曼树创建思路
- 从小到大进行排序,将每一个数据,每个数据都是一个结点,每个结点可以看成是一颗最简单的二叉树
- 取出根结点权重最小的两颗二叉树
- 组成一颗新的二叉树,该新的二叉树的根结点的权值是前面两颗二叉树根结点权值的和
- 再将这颗新的二叉树,以根结点的权值大小再次排序,不断重复1-2-3-4的步骤,直到数列中,所有的数据都被处理,就得到一颗赫夫曼树
4、赫夫曼树代码实例
(1)Node
package com.guor.huffmantree;
public class Node implements Comparable<Node>{
int value;//结点权值
Node left;//指向左子结点
Node right;//指向右子结点
public Node(int value){
this.value = value;
}
@Override
public String toString(){
return "Node [value="+value+"]";
}
@Override
public int compareTo(Node o) {
//表示从小到大排序
return this.value - o.value;
}
//写一个前序遍历
public void preOrder(){
System.out.println(this);
if(this.left != null){
this.left.preOrder();
}
if(this.right != null){
this.right.preOrder();
}
}
}
(2)创建赫夫曼树HuffmanTree
package com.guor.huffmantree;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
public static void main(String[] args) {
int[] arr = {13,7,8,3,29,6,1};
Node root = createHuffmanTree(arr);
//测试
preOrder(root);
}
//编写一个前序遍历的方法
public static void preOrder(Node root){
if(root != null){
root.preOrder();
}else {
System.out.println("空树不能遍历.");
}
}
//创建赫夫曼树的方法
public static Node createHuffmanTree(int[] arr){
List<Node> nodeList = new ArrayList<>();
for(int value : arr){
nodeList.add(new Node(value));
}
//处理的过程是一个循环的过程
while (nodeList.size() > 1){
//从小到大排序
Collections.sort(nodeList);
System.out.println("nodes="+nodeList);
//取出根结点权值最小的两颗二叉树
//1、取出权值最小的结点
Node leftNode = nodeList.get(0);
//2、取出权值第二小的结点
Node rightNode = nodeList.get(1);
//3、构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//4、从list中删除处理过的二叉树
nodeList.remove(leftNode);
nodeList.remove(rightNode);
//5、将parent加入list
nodeList.add(parent);
}
//返回赫夫曼树的root结点
return nodeList.get(0);
}
}
(3)控制台输出
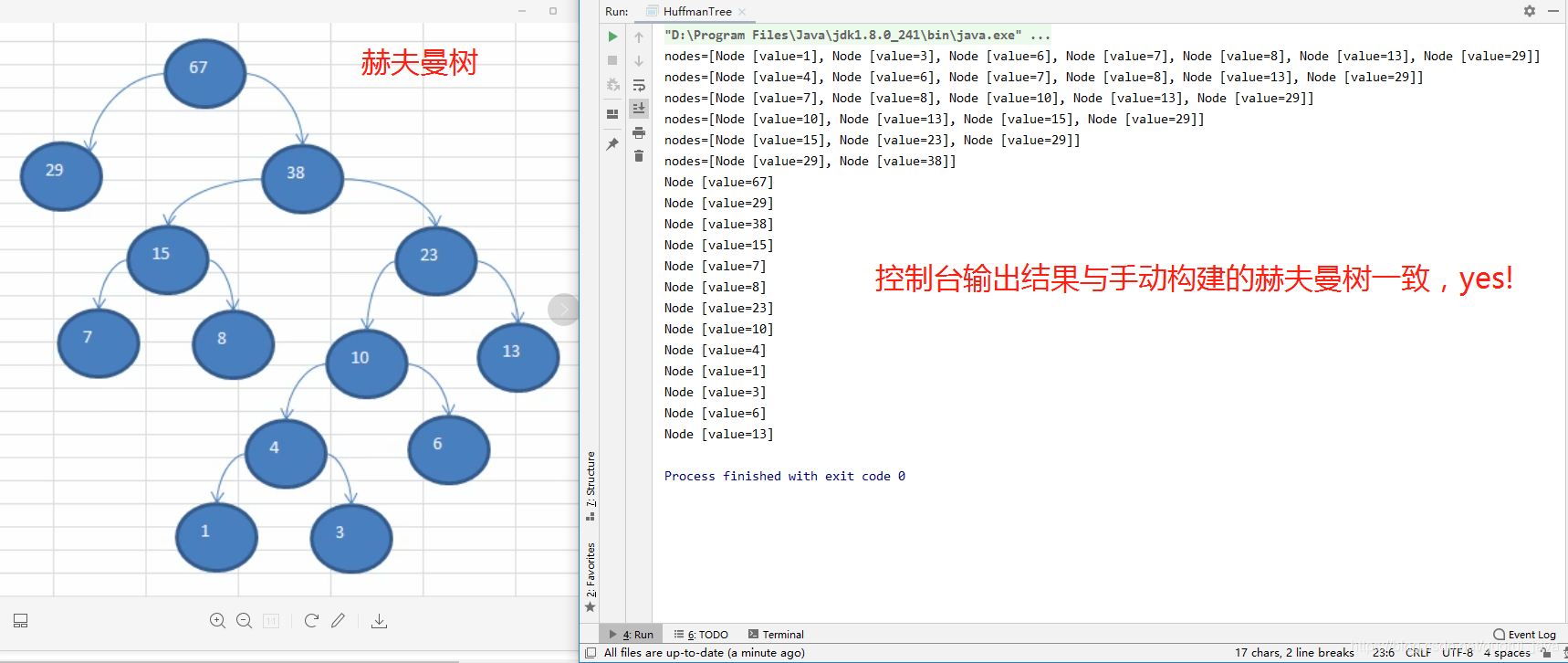
往期精彩内容: