在这里非常感谢这位博主的文章,是他的代码让我理解清楚了很多:
(56条消息) 堆排序C语言实现(源代码)_桃花er的博客-CSDN博客_堆排序c语言代码
堆排序就是将一个数组利用大根堆、小根堆(完全二叉树)的思想来对数组排序。
大根堆:父节点的值大于等于子节点;
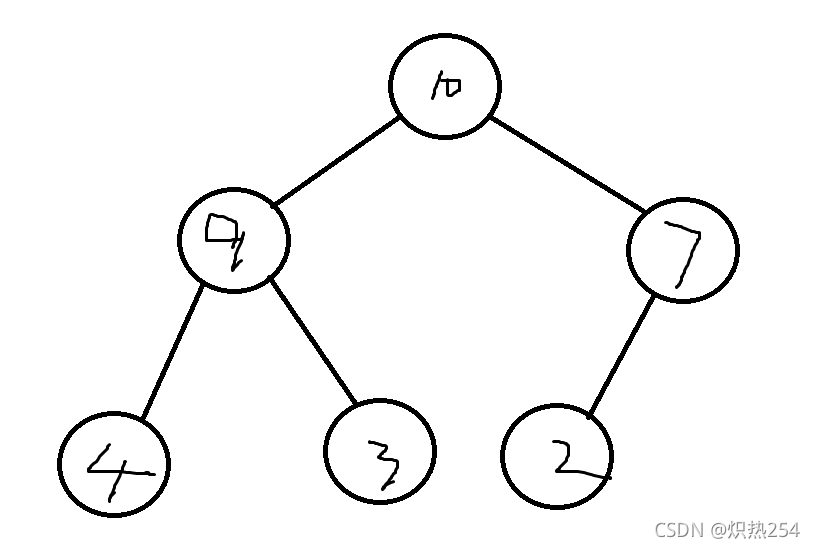
小根堆:父节点的值小于或等于子结点
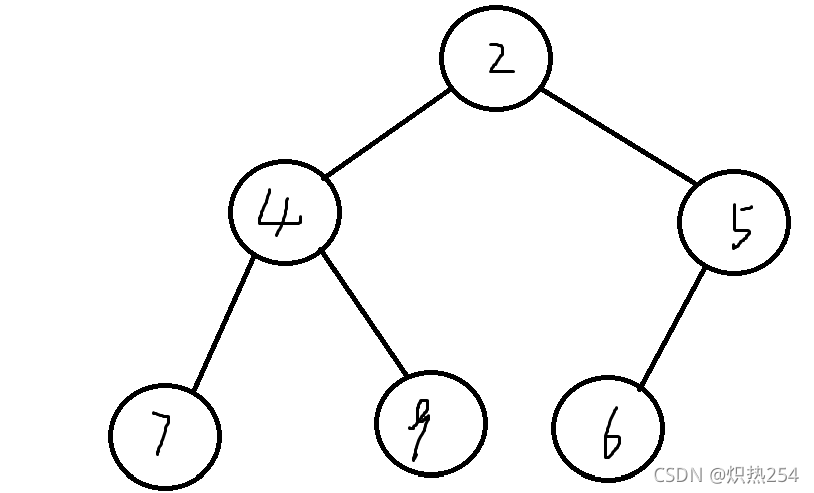
因为完全二叉树的编号正好可以和数组的编号一一对应,这就将对数组的排序转化到了对二叉树的排序。
因此我们就可以将一个任意的数组生成一个完全二叉树
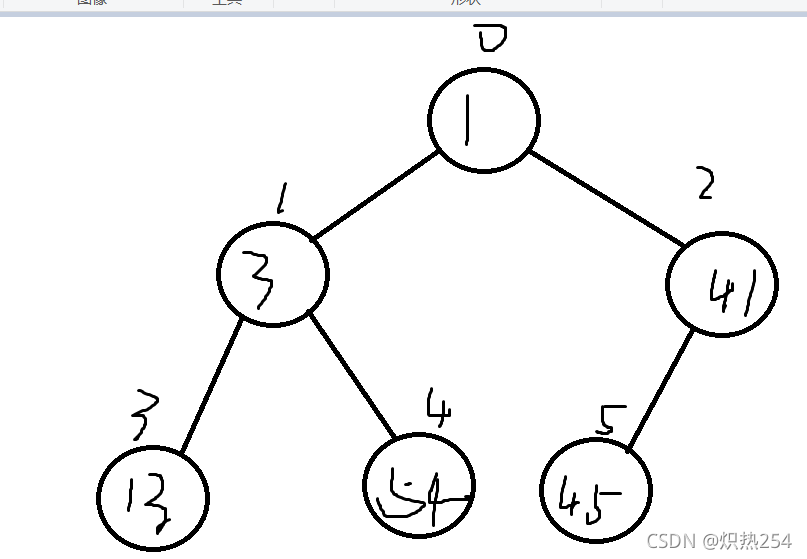
利用小根堆或者大根堆的定义,可以看出他是阐述的关于父节点以及子节点之间的关系。因此在进行排序的时候,二叉树中的叶子节点就不用考虑,而是考虑内部结点以及根节点。在比较的过程中,我们先沿着左孩子区域先比较,后面在比较右孩子(这个比较顺序可以颠倒过来的)
序号最大的一个内部节点下标为:(二叉树中编号最大的叶子节点-1)/2;上图中则有(5-1)2=2;我们就应从2号结点开始,依次对编号为2、1、0的内部节点及其根节点进行排序(此处需要一个循环)。
我以大根堆为例。
首先是二号结点,
此时我们将根节点的编号标记成max(max=2),一旦找到比根节点大的值,我们用max将其坐标记录下来
;由于41<45,交换max,此时max=5,没有右孩子,结束对他的判断;对于1号结点(max=1):3<13,交换(max=3);之后在将最大值与右孩子比较,13<54;继续交换(max=4);
只要max指向了叶子结点,下面就没有孩子,就不用在进行之前的判断
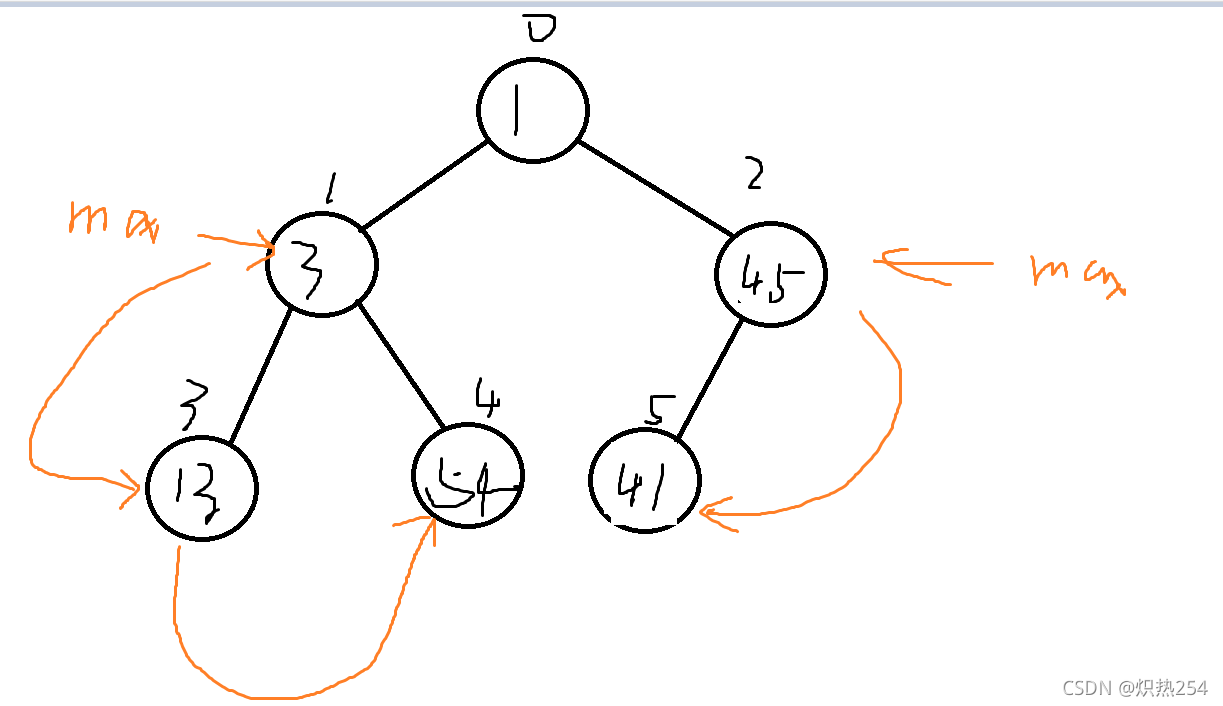
之后再将父节点与孩子中的最大值进行替换(替换条件:max的编号部位父节点)
之后比较根节点处,同样的方法可以得到:此时的max由指向根节点,发生交换后,指向1号结点
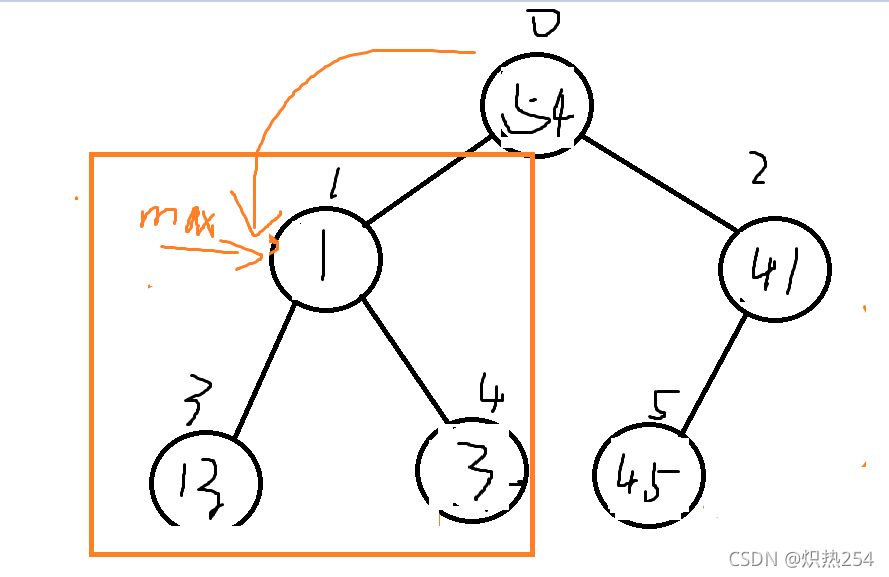
此时由max指向的区域内不满足大跟堆的定义,
继续重复一下之前的操作,直到满足大跟堆的大小关系(递归思想)
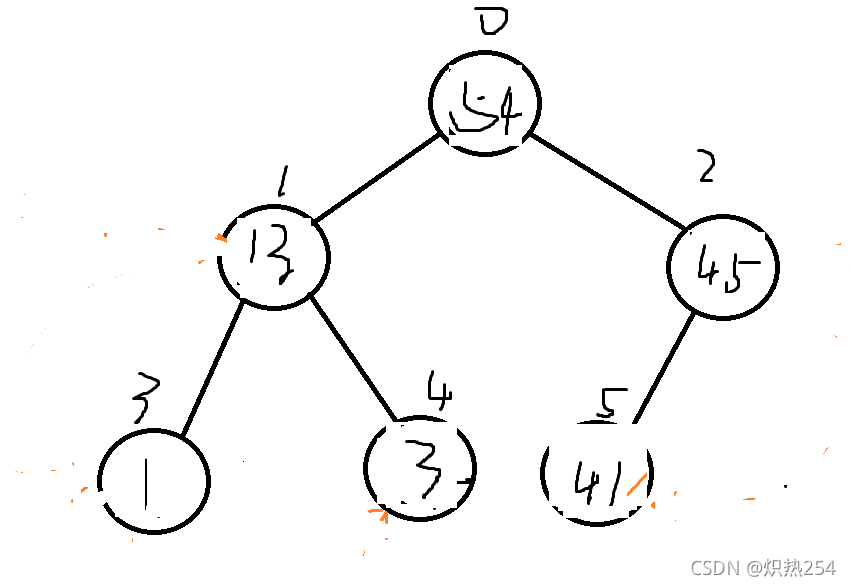
则就可以形成代码:(这个只是针对一个结点进行的操作)
int heapify(int arr[], int n,int i)//n代表元素个数,i代表修改的结点位置
{
if (i >= n)
{
return;
}
int c1 = 2 * i+1;//左孩子编号
int c2 = 2 * i + 2;//右孩子编号
int max = i;
if (c1< n && (arr[c1] >arr[max]))//比较左孩子
{
max = c1;
}
if (c2 < n && arr[c2] > arr[max])//比较右孩子
{
max = c2;
}//以上的两个循环只是为了在父节点,子节点中找出最大的那个值
if (i != max)
{
swap(arr, i, max);//交换,交换后,就要继续判断max作为父节点的子树中是否也需要替换
heapify(arr, n, max);
}
return 1;
}
其中n表示这个函数能够最大操作的结点数
。后面我们还需要对叶子结点之外的进行操作,所以需要设计一个循环,这样就形成了一个大根堆
int build_heap(int arr[], int n)//n代表元素元素,
{
int last = n - 1;
int par = (last - 1) / 2;//编号最大的内部节点
for (par; par >= 0; par--)
{
heapify(arr, n, par);
}
return 1;
}
注意其中的n值决定了要修改的父节点的地方,比如n=5,那么久从2号结点开始;n=4,那么就修改1号结点。结合前面的n的作用:
n表示这个函数能够最大操作的结点数
后面按照升序的原则,位置编号很大的放置值比较大的元素。我们就可以将生成的大根堆的根节点放置在最后一个元素的地方,交换二者的位置。结合前面n的值,此时我们就可以发现,当我们将最大元素放在叶子节点的时候,
我们将修改的元素数量减少1,就可以不用对刚放入的最大元素进行进行修改
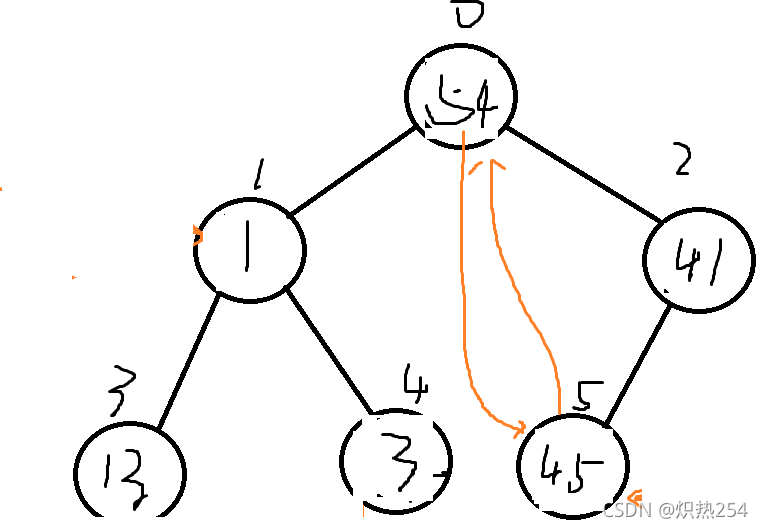
则有代码:
int heap_sort(int arr[], int n)
{
int last = n - 1;
build_heap(arr, n);
for (last; last >= 0; last--)
{
swap(arr, 0, last);
heapify(arr, last, 0);//对不包括大数的剩余结点进行堆化
}
}之后就有
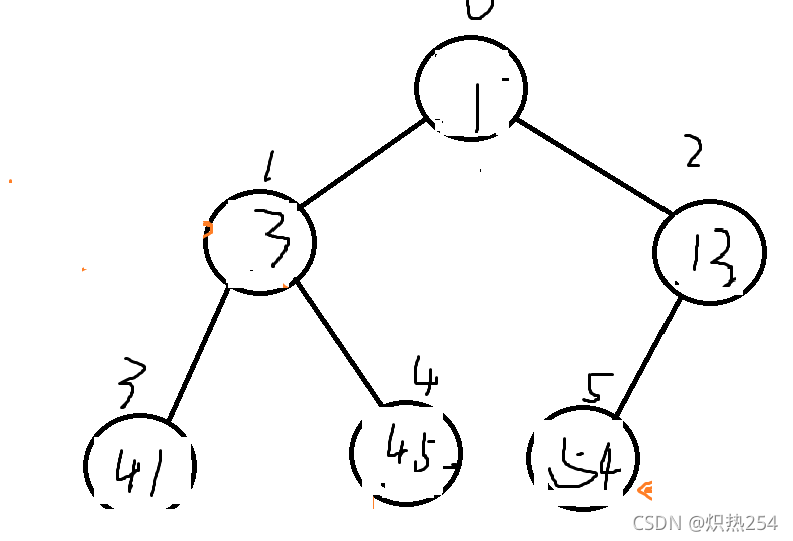
之后这样的按照二叉树的位置序号,依次输出这些值。
要记住:这些只是利用大根堆的思想来排序,实际应该操作的地方是在数组中
全部源码如下:
#include <stdio.h>
void swap(int arr[], int x, int y)
{
int temp = arr[x];
arr[x] = arr[y];
arr[y]=temp;
}
int heapify(int arr[], int n,int i)//n代表元素个数,i代表修改的结点位置
{
if (i >= n)
{
return;
}
int c1 = 2 * i+1;
int c2 = 2 * i + 2;
int max = i;
if (c1< n && (arr[c1] >arr[max]))//通过比较各个结点之间的大小关系,就可以生成对应的根堆,从而实现数组的正逆序
{
max = c1;
}
if (c2 < n && arr[c2] > arr[max])
{
max = c2;
}//以上的两个循环只是为了在父节点,子节点中找出最大的那个值
if (i != max)
{
swap(arr, i, max);//交换,交换后,就要继续看子节点中是否满足
heapify(arr, n, max);
}
return 1;
}
int build_heap(int arr[], int n)//n代表元素元素,
{
int last = n - 1;
int par = (last - 1) / 2;
for (par; par >= 0; par--)
{
heapify(arr, n, par);
}
return 1;
}
int heap_sort(int arr[], int n)
{
int last = n - 1;
build_heap(arr, n);
for (last; last >= 0; last--)//last能够对应到最后一个元素的下标,同样也能够对应到n-1个元素
{
swap(arr, 0, last);
heapify(arr, last, 0);
}
}
void Print(int* arr, int x)
{
int i = 0;
for (i; i < x; i++)
{
printf("%4d", *(arr + i));
}
}
int main()
{
int arr[] = { 1,3,41,13,54,65 };
int len = sizeof(arr) / sizeof(arr[0]);
Print(arr, len);
printf("\n");
heap_sort(arr, len);
Print(arr, len);
return 0;
}
推荐一个Up主的视频: