数据结构——图的最短路径算法(Dijkstra&Floyd)

#include<iostream>
#include<time.h>
#include<Windows.h>
#include< queue>
using namespace std;
#define NUM 100
#define TURE 1
#define FLASE 0
#define INAVAIL -1
#pragma warning(disable:4996)
typedef struct link
{
	int index;
	int distance;
	struct link *next;
}*Node, node;
typedef struct Link
{
	char word;
	Node first;
}*Head, head;
typedef struct g
{
	head linktable[NUM];
	int n, e;
}*Map, map;
typedef struct dj
{
	int dis[NUM];
	int pre[NUM];
	int avail[NUM];
}*DJtable, djtable;
typedef struct fl
{
	int Distance[NUM][NUM];
	int Midnode[NUM][NUM];
}*FLtable,fltable;
void Allocatemap(Map &G);//给图指针分配一块图的专属区域
void Parmmap(Map G);//传入邻接表参数
void Createmap(Map G);//创建邻接表表头
int Locatev(Map G, char x);//确定关系顶点的位置
void Relatemap(Map G);//创建图的关系链
void Printmap(Map G);//打印图的邻接表
void DJcreatetable(Map G,DJtable &T,char outset);//初始化迪杰斯特拉算法的最短路径表
int DJfindminsize(Map G, DJtable T);//根据迪杰斯特拉算法寻找表中未被确认最优点中的最短路径并将其归入最优点
void DJfindminpath(Map G, DJtable T,char outset);//根据迪杰斯特拉算法寻找各点的最优路径
void DJprinttable(Map G, DJtable T);//根据迪杰斯特拉算法打印最短路径表
void DJsearchpath(Map G, DJtable T, int outset, int end);//根据迪杰斯特拉算法的最短路径表寻找规定两点间的最短路径
void DJprintpath(Map G, DJtable T, int outset, int end);//在迪杰斯特拉算法的基础上打印两点间最短路径及其距离
void FLcreatetable(Map G, FLtable &T);//初始化弗洛伊德算法的最短路径表
void FLfindminpath(Map G, FLtable T);//根据弗洛伊德算法改善最短路径表
void FLprinttable(Map G, FLtable T);//根据弗洛伊德算法打印距离表和中间节点表两个二维数组
void FLprintpath(Map G, FLtable T, int outset, int end);//在弗洛伊德算法的基础上打印两点间最短路径及其距离
int main()
{
	Map G;
	DJtable DJT ;
	FLtable FLT;
	char outset,end;
	Allocatemap(G);
	Parmmap(G);
	Createmap(G);
	Relatemap(G);
	Printmap(G);
	cout << "请输入您要查找最短路径的终点和起点：";
	cin >> outset >> end;
	DJcreatetable(G,DJT,outset);
	DJfindminpath(G, DJT, outset);
	DJprinttable(G, DJT);
	DJprintpath(G, DJT, Locatev(G, outset), Locatev(G, end));
	FLcreatetable(G, FLT);
	FLfindminpath(G, FLT);
	FLprinttable(G, FLT);
	FLprintpath(G, FLT, Locatev(G, outset), Locatev(G, end));
	return 0;
}
void Allocatemap(Map &G)//给图指针分配一块图的专属区域
{
	G = new map;
}
void Parmmap(Map G)//传入邻接表参数
{
	cout << "请输入图的基本参数，即图的顶点数和边数：";
	cin >> G->n;
	cin >> G->e;
}
void Createmap(Map G)//创建邻接表表头
{
	char a[NUM];
	cout << "请输入顶点的具体数据：";
	cin >> a;
	for (int i = 0; i < G->n; i++)
	{
		G->linktable[i].word = a[i];
		G->linktable[i].first = NULL;
	}
}
int Locatev(Map G, char x)//确定关系顶点的位置
{
	int i;
	for (i = 0; i < G->n; i++)
	{
		if (G->linktable[i].word == x) return i;
	}
	return -1;
}
void Relatemap(Map G)//创建图的关系链
{
	int j = 0, k = 0;
	char a, b;
	int c = 0;
	cout << "请输入图的关系以及相应带权：" << endl;
	for (int i = 0; i < G->e; i++)
	{
		cin >> a >> b >> c;
		j = Locatev(G, a);
		k = Locatev(G, b);
		Node p = new node;
		p->index = k;
		p->distance = c;
		p->next = G->linktable[j].first;
		G->linktable[j].first = p;
	}
}
void Printmap(Map G)//打印图的邻接表
{
	cout << "图的邻接表为：" << endl;
	for (int i = 0; i < G->n; i++)
	{
		Node p = G->linktable[i].first;
		cout << G->linktable[i].word << "--->";
		while (p)
		{
			cout << G->linktable[p->index].word << "  ";
			cout << p->distance;
			p = p->next;
			if (p)cout << "-->";

		}
		cout << endl;
	}
}
void DJcreatetable(Map G, DJtable &T,char outset)//初始化迪杰斯特拉算法的最短路径表
{
	int begin = Locatev(G, outset);
	T = new djtable;
	for (int i = 0; i < G->n; i++)
	{
		T->dis[i] = INT_MAX;
	}
	T->dis[begin] = 0;
	for (int i = 0; i < G->n; i++)
	{ 
	T->pre[i] = 0;
	}
	T->pre[begin] = -1;
	for (int i = 0; i < G->n; i++)
	{ 
	T->avail[i] = { 0 };
	}
	T->avail[begin] = TRUE;
}
int DJfindminsize(Map G, DJtable T)//根据迪杰斯特拉算法寻找表中未被确认最优点中的最短路径并将其归入最优点
{
	int min;
	for (int i = 0; i < G->n; i++)
	{
		if (T->avail[i] == FALSE)
		{
			min = i;
			break;
		}
	}
	for (int i = 0; i < G->n; i++)
	{
		if (T->avail[i] == FALSE&& T->dis[i] < T->dis[min])
			min = i;
	}
	T->avail[min] = TRUE;
	return min;
}
void DJfindminpath(Map G, DJtable T,char outset)//根据迪杰斯特拉算法寻找各点的最优路径
{
	int newavail = Locatev(G,outset);
	if(!G->linktable[newavail].first)return ;
	for (int i = 1; i < G->n; i++)
	{
		Node p = G->linktable[newavail].first;
		if (!p)break;
		while (p)
		{
			if (T->dis[p->index] > p->distance + T->dis[newavail])
			{
				T->dis[p->index] = p->distance + T->dis[newavail];
				T->pre[p->index] = newavail;
			}
			p=p->next;
		}
		newavail = DJfindminsize(G, T);
	}
}
void DJprinttable(Map G, DJtable T)//根据迪杰斯特拉算法打印最短路径表
{
	cout << "迪杰斯特拉算法最短路径表为：" << endl;
	for (int i = 0; i < G->n; i++)
	{
		if (i != 0)cout << "    ";
		cout << G->linktable[i].word;
	}
	cout << endl;
	for (int j = 0; j < G->n; j++)
	{
		if (j != 0&&T->dis[j-1]>=10)cout << "   ";
		else if (j != 0)cout << "    ";
		cout << T->dis[j];
	}
	cout << endl;
	for (int k = 0; k < G->n; k++)
	{
		if (k != 0 && k - 1 == 0)cout << "   ";
		else if (k != 0)cout << "    ";
		cout << T->pre[k];
	}
	cout << endl;
	for (int l = 0; l < G->n; l++)
	{
		if (l != 0)cout << "    ";
		cout << T->avail[l];
	}
	cout << endl;
}
void DJsearchpath(Map G, DJtable T,int outset,int end)//根据迪杰斯特拉算法的最短路径表寻找规定两点间的最短路径
{
	if (T->dis[end] == INT_MAX)
	{
		cout << "无最短路径";
		return ;
	}
	if (end == outset)cout << G->linktable[outset].word;
	else 
	{
		DJsearchpath(G, T, outset,T->pre[end]);
		cout << "->" << G->linktable[end].word;
	}
}
void DJprintpath(Map G, DJtable T, int outset, int end)//在迪杰斯特拉算法的基础上打印两点间最短路径及其距离
{
	cout <<"根据迪杰斯特拉算法得出"<<G->linktable[outset].word << "点到" << G->linktable[end].word << "点的最短路径为：";
	DJsearchpath(G, T, outset, end);
	cout << endl << "最短路径的距离为：";
	if (T->dis[end] == INT_MAX)cout << "∞"<<endl;
	else cout<<T->dis[end]<<endl;
}
void FLcreatetable(Map G, FLtable &T)//初始化弗洛伊德算法的最短路径表
{
	T = new fltable;
	for (int i = 0; i < G->n; i++)
	{
		for (int j = 0; j < G->n; j++)
		{
			Node p = G->linktable[i].first;
			if (i == j)
			{
				T->Distance[i][j] = INAVAIL;
				T->Midnode[i][j] = INAVAIL;
			}
			else
			{
				while (p)
				{
					if (p->index == j)
					{
						T->Distance[i][j] = p->distance;
						break;
					}
					p = p->next;
				}
				if (!p)T->Distance[i][j] = INT_MAX;
				T->Midnode[i][j] = j;
			}	
		}
	}
}
void FLfindminpath(Map G, FLtable T)//根据弗洛伊德算法改善最短路径表
{
	for (int k = 0; k < G->n; k++)
	{
		for (int i = 0; i < G->n; i++)
		{
			for (int j = 0; j < G->n; j++)
			{
					if (i == k)break;
					else if (i == j || j == k || T->Distance[i][k] == INT_MAX || T->Distance[k][j] == INT_MAX)continue;
					else if (T->Distance[i][j] > T->Distance[i][k] + T->Distance[k][j])
					{
						T->Distance[i][j] = T->Distance[i][k] + T->Distance[k][j];
						T->Midnode[i][j] = T->Midnode[i][k];
				    }
			}
		}
	}
}
void FLprinttable(Map G, FLtable T)//根据弗洛伊德算法打印距离表和中间节点表两个二维数组
{
	cout << "弗洛伊德算法各点间最短路径表为：" << endl;
	for (int i = 0; i < G->n; i++)
	{
		if (i == 0)cout << "   ";
		cout << G->linktable[i].word << "  ";
	}
	cout << endl;
	for (int i = 0; i < G->n; i++)
	{
		cout << G->linktable[i].word << "  ";
		for (int j = 0; j < G->n; j++)
		{
			if (j != 0)cout << " ";
			if (T->Distance[i][j] != INT_MAX && T->Distance[i][j] < 10 && T->Distance[i][j] >= 0)cout << " " << T->Distance[i][j];
			else if (T->Distance[i][j] == INT_MAX)cout << "∞";
			else cout << T->Distance[i][j];
		}
		cout << endl;
	}
	for (int i = 0; i < G->n; i++)
	{
		if (i == 0)cout << "   ";
		cout << G->linktable[i].word << "  ";
	}
	cout << endl;
	cout << "弗洛伊德算法各点中间结点表为：" << endl;
	for (int i = 0; i < G->n; i++)
	{
		cout << G->linktable[i].word << "  ";
		for (int j = 0; j < G->n; j++)
		{
			if (j != 0)cout << "  ";
			cout << T->Midnode[i][j];
		}
		cout << endl;
	}
}
void FLprintpath(Map G, FLtable T,int outset,int end)//在弗洛伊德算法的基础上打印两点间最短路径及其距离
{
	int DIS = T->Distance[outset][end];
	cout <<"根据弗洛伊德算法得出"<<G->linktable[outset].word << "点到" << G->linktable[end].word << "点的最短路径为：";
	if (DIS== INT_MAX)
	{
		cout << "无最短路径";
		cout << endl << "最短路径的距离为：∞"<<endl;
		return;
	}
	while (1)
	{
		if (outset == end)break;
		cout << G->linktable[outset].word << "->";
		outset = T->Midnode[outset][end];
	}
	cout << G->linktable[outset].word;
	cout << endl << "最短路径的距离为：" << DIS<<endl;
}
在这里插入图片描述

上图左图是有向图演示示例的逻辑结构图，右图是对应图的邻接表

【小结】：①迪杰斯特拉算法求解图的最短路径核心思想就是贪心算法，在每一次寻找存在的相邻结点后，都会确定一个此时的最优结点，直到所有结点都被确认为最优点为止。此算法常被用于解决单源路径最短问题，时间复杂度为O(n^2)。

②弗洛伊德算法求解图的最短路径核心思想就是动态规划，即不断的寻找两个结点之间是否存在中间节点可以使路径更短，经过不断的更新迭代，得到所有结点之间最短路径的最优解。此算法常被用于解决多源路径最短问题，也称之为3for算法，时间复杂度为O(n^3)。

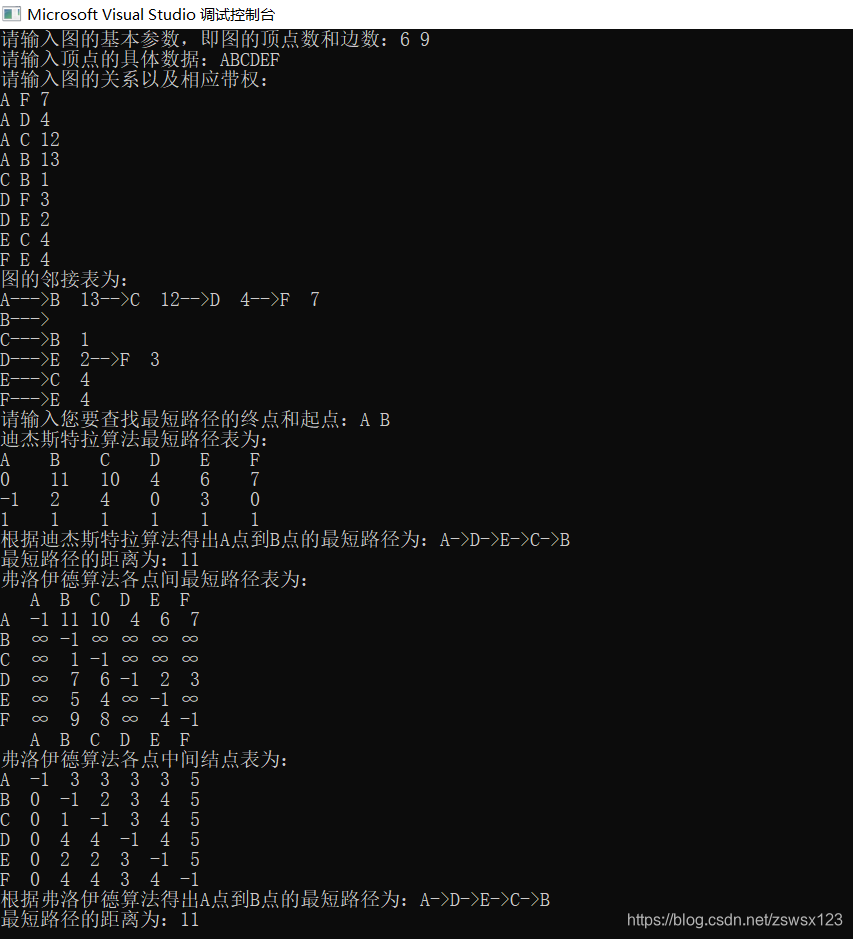
下图是对应代码的运行结果

在这里插入图片描述
原文链接：https://blog.csdn.net/zswsx123/article/details/115579217
你可能也喜欢
