堆排序,首先要理解堆的概念,
堆是由树组成,首先需要涉及到的概念就是,树,二叉树,完全二叉树。,大根堆,小根堆,
可根据别的网站搜索或者
https://www.jb51.net/article/216519.htm
访问可知上述的答案:
然后 大根堆:所有的孩子节点没有自己大的的完全二叉树:
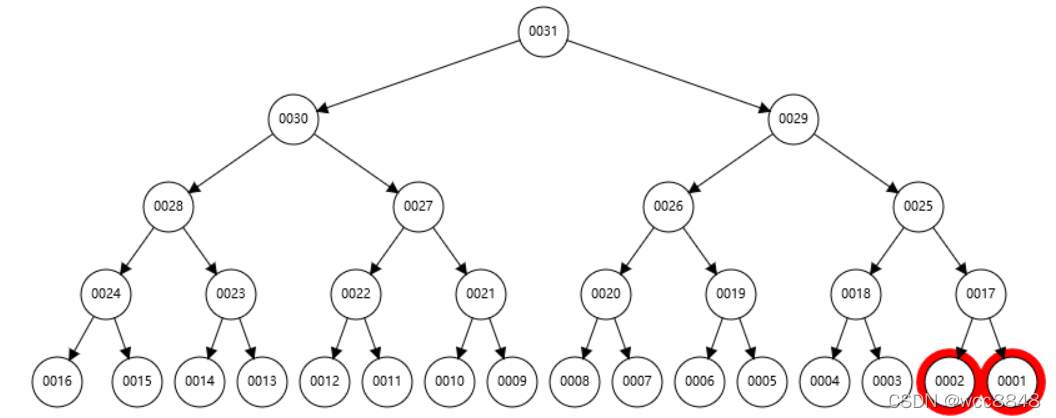
小根堆:
所有的孩子节点都比自己大的完全二叉树:
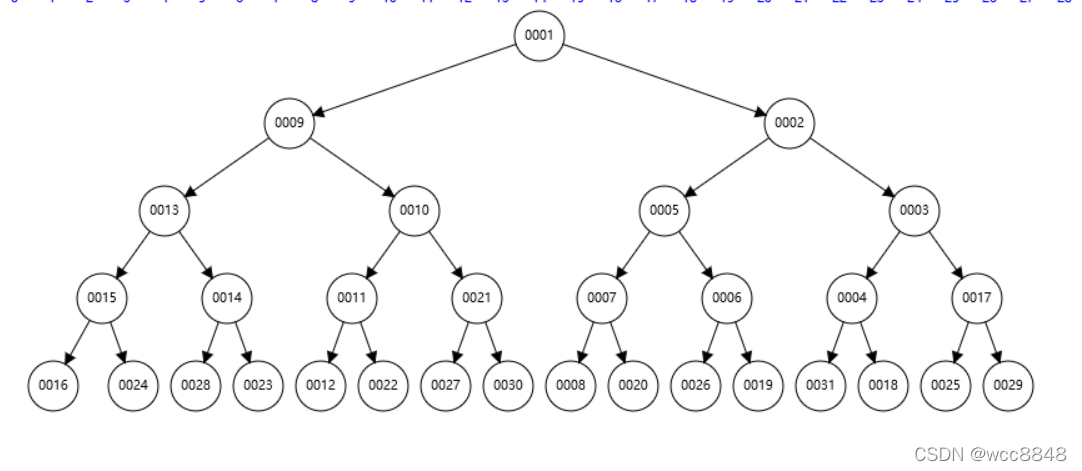
然后了解堆的自我调整:
#构建一个堆 #1.建立堆 #2.得到堆顶元素,为最大元素 #3.去掉堆顶,将堆最后一个元素放到堆顶,此时可以通过一次调整重新使堆有序 #4.堆顶元素为第二大元素 #5.重复步骤3,直到堆变空
建立堆
def sift(li,low,high):
'''
:param li: 列表
:param low: 堆的根结点位置
:param high:堆的最后一个元素的位置,
:return:
'''
i = low #最开始指向根节点
j = 2*i+1 #j开始是左孩子
temp = li[low]##存储堆顶元素
while j <= high: #只要j位置有数
if j+1<=high and li[j+1]>li[j]:#边界的判定条件,如果右孩子比较大
j =j+1 #j指向右孩子
if li[j]>temp:大于堆顶元素
li[i] = li[j]交换
i = j
j = 2*i+1
else:##如果temp放入i的地方
li[i] =temp#把temp放入某一节领导的位置
break
else:
li[i] =temp##把temp放到叶子节点上
然后进行排序:
def heap_sort(li):
n = len(li)
for i in range((n-2)//2,-1,-1):
#i表示建堆的时候调整的部分的根下表
sift(li ,i,n-1)
##建堆就完成了
for i in (n-1,-1,-1):##当前堆的最后一个元素
li[0],li[i] = li[i],li[0]
sift(li,0,i-1)##i-1是新的high
版权声明:本文为wcc8848原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。