字符串匹配的算法想必大家都见得多了。之前在看《算法设计与分析基础》一书的时候,书中介绍了BoyerMoore算法和大名鼎鼎的KMP算法,当时只是用Swift实现了一遍。今天在尝试用Python编写KMP的时候,无意中看到Sunday算法,该算法的编写比BoyerMoore简单,也比BoyerMoore快,更是胜过KMP,这里就把这三种方法总结一下。
KMP算法
关于KMP算法,我是直接看的
阮一峰
的博客然后实现的。该博客中对于KMP算法有一个深入浅出的讲解。这里还是借阮一峰的博文简单说一下KMP算法。
Python代码Github地址
首先,如果我们试图匹配一个长字符串”BBC ABCDAB ABCDABCDABDE”和一个短字符串”ABCDABD”。

首先长字符串的B和短字符串的A不匹配,短字符串后移一位。

B和A还是不匹配,搜索词继续后移。直到字符串有一个字符与搜索词的第一个字符相同为止。然后继续匹配,这时候我们可以看到下面的匹配表:

此时发现长字符串的” “和短字符串的D不同,这时候我们如果还是把短字符串直接后移一位,效率就会非常低。此时我们应该注意到,前面的六个字符ABCDAB已经匹配上了,同时因为AB在这六个字符中出现了两次,我们能否把前面的AB直接后移到后面的这个AB处呢?

我们把短字符串后移了4个位置,那么这四个位置是怎么求出来的呢?我们可以注意到,在前一张图中,我们已经匹配了六个字符,而最后两位匹配字符和短字符串的前两个字符相等,这样我们就会有6-4=2。根据这一规律,我们可以构建一个移位表,表中的每个字符对应数值等于
目前已经匹配长度-部分匹配值
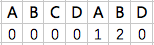
部分匹配值就是短字符串的“前缀”和“后缀”的共同长度,其表如下所示:
比如我们来看字符串AB,AB的前缀为A,后缀为B两者不相等,所以共有元素为0
字符串ABCDA的前缀有[A, AB, ABC, ABCD],后缀有[BCDA, CDA, DA, A],共有的部分是A,所有部分匹配值是1,同样可以求得ABCDAD的共有部分是AB,部分匹配值为2。
构建部分匹配值表的代码如下:
def matchTable(aList):
length = len(aList)
table = [0]*length
index = 1
while index < length:
sameLen = 0
while aList[:sameLen+1] == aList[index:index+sameLen+1]:
sameLen += 1
table[index+sameLen-1] = sameLen
if sameLen != 0:
index += sameLen
else:
index += 1
return table
我们可以测试一下字符串
'abcdabcdaabbaac'
,得到的部分匹配值表为[0, 0, 0, 0, 1, 2, 3, 4, 5, 1, 2, 0, 1, 1, 0]。
有了部分匹配值表,接下来的工作就非常简单了,每次从头到尾扫描,如果第一个字符就不匹配,直接后移一位,如果前缀存在字符匹配,但最终字符不匹配,那么就是用公式目前已匹配值-查表得到的部分匹配值,就是字符串需要后移的长度。直至搜索到结尾。
整体代码如下:
def kmp(str1, str2):
if str1 == None or str2 == None or len(str1) < len(str2):
return False
index = 0 # index为str2对应于每次开始的位置
len1, len2 = len(str1), len(str2)
moveTable = matchTable(list(str2))
pAppear = []
while index <= len1 - len2:
tmpIndex = 0 # tmpIndex为str2中字符走到的位置
while tmpIndex < len2 and str1[index+tmpIndex] == str2[tmpIndex]:
tmpIndex += 1
if tmpIndex == len2:
pAppear.append(index)
index += len2
continue
elif tmpIndex > 0:
index += tmpIndex - moveTable[tmpIndex-1]
else:
index += 1
return pAppear if pAppear else False
# 生成KMP匹配表, 该表和next表不一样
def matchTable(aList):
length = len(aList)
table = [0]*length
index = 1
while index < length:
sameLen = 0
while aList[:sameLen+1] == aList[index:index+sameLen+1]:
sameLen += 1
table[index+sameLen-1] = sameLen
if sameLen != 0:
index += sameLen
else:
index += 1
return table我对KMP算法进行了简单的修改,不只是输出是否存在字符串,而且存在多个相同子字符串的话,输出每一个相同子字符串的首字符位置。但是对于查找aaaaa中的aa的话,只会输出[0, 2]。主要是个人理解的问题,你也可以修改一下相关代码,使得在aaaaa中查找aa的话,输出的是[0, 1, 2, 3]。
BoyerMoore算法
BoyerMoore算法是Horspool算法的改进版本。BM算法的代码比KMP的算法复杂,但是运行速度快于KMP算法。BM算法的关键在于构建一个坏符号移动表和一个好后缀移动表。
Python代码GitHub
还是看一个
阮一峰
大神的博客。。。那叫一个深入浅出!
先上一个总表:

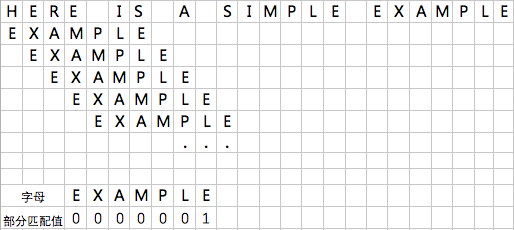
首先是字符串与搜索词头部对其,从尾部开始比较。这是一个很聪明在的做法,因为如果尾部不匹配,那么只需要一次比较即可,就指到前7个字符肯定不是要找的结果。我们看到S和E不匹配,S就被称为坏字符,而且S不在EXAMPLE中,那么整个字串就可以直接移到S的后面。
然后是第二行的EXAMPLE,E和P不相同,这时候我们就不能直接把字符后移到P的后面,因为P这个字符也出现在EXAMPLE中了。P作为一个坏字符,这里把字符串后移两位,让两个P对齐,继续开始比较。那我们如何确定每个坏字符对应后移多少位呢?我们假设短字串的长度为m,坏字符表字符对应:
1. 短字串的长度(如果坏字符c不包含在短字串的前m-1个字符中)
2. 短字串m-1个字符中最右边的c到模式最后一个字符的距离(在其他情况下)
3.
移动距离 = 坏字符表中对应数字 – 当前已匹配后缀长度
具体到这个例子中,EXAMPLE对应的坏字符表为654321。比如如果EXAMPLE的最后面一个E对应的一个坏字符是L,那么我们只需要把字符串后移一位,如果最后一个E对应的坏字符是P,我们把字符串后移2位。这里需要特别注意的是,移动的距离等于最右边的c到
最后一个字符
的距离,而不是到最后的距离。而其他不出现在字符串中的字符,移动长度都为字符串的长度,比如上面举到的例子S,移动距离就是7-0 = 7。
坏字符表代码如下:
def badCharTable(pattern):
table = {}
length = len(pattern)
alphaBet = list(map(chr, range(32, 127))) # 利用map生成一个原始移动表, 对应字符为从SPACE到~, 使用UTF-8对应表
for i in alphaBet:
table[i] = length
# 更改pattern中存在字符的对应移动距离
for j in range(length-1):
table[pattern[j]] = length - 1 - j
return table
说完了坏字符表,再看一下好后缀表。当第三次匹配的时候,我们可以看到对于EXAMPLE,从后往前我们的MPLE都匹配上了,只是到A的时候匹配失败,这时候,我们称MPLE是一个好后缀(good suffix),注意,MPLE,PLE,LE和E都是好后缀。
当I与A不匹配的时候,I是坏字符,根据坏字符规则,I在坏字符表中对应7,当前已匹配4个字符,那么应该后移7-4=3个字符。就像上图第三行所示。
那是否有更好的移动方法呢?这里就需要引入
好后缀规则
的概念。
后移位数 = 好后缀的位置 – 搜索词中的上一次出现位置
举例来说,如果字符串“ABCDAB”的后一个“AB”是“好后缀”。那么它的位置是5(从0开始计算,取最后的“B”的值),在“搜索词中的上一次出现位置”是1(第一个”B”的位置),所以后移 5 – 1 = 4位,前一个”AB”移到后一个”AB”的位置。
再举一个例子,如果字符串“ABCDEF”的“EF”是好后缀,则“EF”的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 – (-1) = 6位,即整个字符串移到”F”的后一位。
这个规则有三个注意点:
(1)“好后缀”的位置以最后一个字符为准。假定“ABCDEF”的“EF”是好后缀,则它的位置以“F”为准,即5(从0开始计算)。
(2)如果“好后缀”在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,“EF”在“ABCDEF”之中只出现一次,则它的上一次出现位置为-1(即未出现)。
(3)如果”好后缀”有多个,则除了最长的那个”好后缀”,其他”好后缀”的上一次出现位置必须在头部。比如,假定“BABCDAB”的“好后缀”是“DAB”、“AB”、“B”,请问这时”好后缀”的上一次出现位置是什么?回答是,此时采用的好后缀是“B”,它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个”好后缀”只出现一次,则可以把搜索词改写成如下形式进行位置计算“(DA)BABCDAB”,即虚拟加入最前面的“DA”。
回到上文的这个例子。此时,所有的“好后缀”(MPLE、PLE、LE、E)之中,只有“E”在“EXAMPLE”还出现在头部,所以后移 6 – 0 = 6位。
我们可以看到,坏字符规则这能移动3位,好后缀规则如第四行,可以后移6位,所以取6位。总结起来就是,
1. 当从后往前匹配长度为0的时候,采用坏字符移动距离
2. 当匹配长度大于0的时候,取坏字符规则和好后缀移动规则的最大值。
比如上面移动6位后,E和P不匹配,匹配长度为0,按照坏字符移动规则,移动2位。
BM整体代码如下:
def BoyerMoore(original, pattern):
if original == None or pattern == None or len(original) < len(pattern):
return None
len1, len2 = len(original), len(pattern)
pAppear = []
# 查找一个字符使用蛮力法即可
if len2 == 1:
for i in range(len1):
if original[i] == pattern[0]:
pAppear.append(i)
else:
badTable = badCharTable(pattern)
goodTable = goodSuffixTable(pattern)
index = len2 - 1
while index < len1:
indexOfP = len2 - 1
while index < len1 and pattern[indexOfP] == original[index]:
if indexOfP == 0:
pAppear.append(index)
index += len2 + 1
indexOfP += 1
continue
index -= 1
indexOfP -= 1
if index < len1:
index += max(goodTable[len2 - 1 - indexOfP], badTable[original[index]])
return pAppear if pAppear else False
'''
生成一个坏字符表, 移动距离分为两种
字符不在模式中, 移动的长度为模式的长度;
字符在模式中,移动的长度为模式中最右边对应待检测字符对应的模式中存在的此字符到最后一个字符的距离
对于BARBER,除了E,B,R,A的单元格分别为1,2,3,4之外,所有字符移动的单元格均为6
'''
def badCharTable(pattern):
table = {}
length = len(pattern)
alphaBet = list(map(chr, range(32, 127))) # 利用map生成一个原始移动表, 对应字符为从SPACE到~, 使用UTF-8对应表
for i in alphaBet:
table[i] = length
# 更改pattern中存在字符的对应移动距离
for j in range(length-1):
table[pattern[j]] = length - 1 - j
return table
'''
生成一个好后缀表
'''
def goodSuffixTable(pattern):
length = len(pattern)
tabel = [0] * length
lastPrefixPosition, i = len(pattern), length - 1
while i >= 0:
if isPrefix(pattern, i):
lastPrefixPosition = i
tabel[length - 1 - i] = lastPrefixPosition - i + length - 1
i -= 1
for i in range(length-1):
slen = suffixLength(pattern, i)
tabel[slen] = length - 1 - i + slen
return tabel
'''
判断模式后面几个字符是否等于模式前面相应长度的字符
'''
def isPrefix(pattern, p):
length, j = len(pattern), 0
for i in range(p, length):
if pattern[i] != pattern[j]:
return False
j += 1
return True
'''
判断前缀以及后缀的重复长度
'''
def suffixLength(pattern, p):
length, samLen = len(pattern), 0
i, j = p, length-1
while i >= 0 and pattern[i] == pattern[j]:
samLen += 1
i -= 1
j -= 1
return samLen
print(BoyerMoore('aaaaa', 'aa'))
Sunday算法
相比于KMP方法的效率略显低下(当然再低下也甩出Brute Force几条街),和BM算法的超长代码,Sunday算法可是做到了高效和简单。要不能叫Sunday算法呢,就是突出一个爽!
Python代码
还是参照上面那个例子来介绍Sunday算法。
首先我们确定了个指针1和2,分别指向短字符串的开头位置和结尾后面的一个位置。然后指针1开始遍历两个字符串,如果1所指的位置字符不一样,这是后我们判断2处所指的字符(这里是空格)是否在短字符串中。如果存在的话,就把短字符串中的这个对应的字符移动的2指针的位置,再从头开始匹配,如果不存在的话就将短字符串整体移动到2指针之后的这个位置继续进行匹配。
因此,我们也需要构建一个移动表,来记录短字符串的字符以及2指针对应相应字符时移动的距离。比如这个例子中,如果2指针所指为E,则短字符串后移1位,如果为L后移两位。那么,很容易得到公式:
后移距离 = 最右边不重复字符到字符串末尾的距离
代码如下
def matchDict(aList):
moveDict = {}
length = len(aList)
for i in range(length-1, -1, -1):
if aList[i] not in moveDict.keys():
moveDict[aList[i]] = length - i
return moveDict

经过上面不匹配的2指针所指空格移动后,EXAMPLE对应的到了长字串的A处,指针1和指针2也相应的发生了改变。这时继续从1指针遍历字符串,发现还是不行,这时2指针所指的位置对应是E,这时候只能把EXAMPLE后移1位,以免发生如果2指针对齐到前一个E错过中间可能匹配的情况。
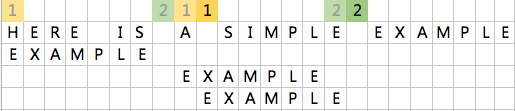
这时候发现还是没有匹配成功,此时2指针所指位置为空格,还是不在段字符串中,因此整体字符串后移到2指针之后。匹配成功。
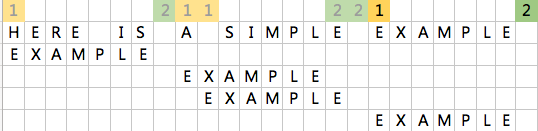
整体代码如下:
def Sunday(str1, str2):
if str1 == None or str2 == None or len(str1) < len(str2):
return None
len1, len2 = len(str1), len(str2)
pAppear, moveDict = [], matchDict(list(str2))
indexStr1 = 0
while indexStr1 <= len1 - len2:
indexStr2 = 0
while indexStr2 < len2 and str1[indexStr1 + indexStr2] == str2[indexStr2]:
indexStr2 += 1
if indexStr2 == len2:
pAppear.append(indexStr1)
indexStr1 += len2
continue
if indexStr1 + len2 >= len1:
break
elif str1[indexStr1+len2] not in moveDict.keys():
indexStr1 += len2 + 1
else:
indexStr1 += moveDict[str1[indexStr1+len2]]
return pAppear if pAppear else False
def matchDict(aList):
moveDict = {}
length = len(aList)
for i in range(length-1, -1, -1):
if aList[i] not in moveDict.keys():
moveDict[aList[i]] = length - i
return moveDict
结论
通过上面的例子我们也可以看到,同样的例子,BM算法比Sunday算法多匹配了一次。而KMP算法呢,匹配了18次。
此外,由于BM算法需要建立一个坏字符表和一个好后缀表,Sunday算法只需要建立一个位移表(可以用hash实现,更加快速)。所以在进行字符串匹配的时候,首选Sunday算法,但是鉴于BM算法代码比较繁琐,所以KMP和BM算法就两者择其一就好。