1.强连通和强连通图
简介:在有向图G中,如果两个顶点互通,称两个顶点强连通(strongly connected)。如果有向图G的两两都强连通,称G是一个强连通图。非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components)。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量,总共三个强连通分量。
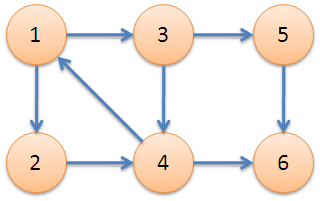
算法1:直接根据定义,用双向遍历取交集的方法求强连通分量,时间复杂度为O(N^2+M)。
算法2:更好的方法是Kosaraju算法或Tarjan算法,两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。
2.[Tarjan算法]
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。DFN[] 数组存储访问顺序,也就是先遍历的点,会先分配一个的序号(小到大),然后序号存在这个数组当中。如:DFN(u)为节点u搜索的次序编号(时间戳)Low[] 表示该点所能直接或间接达到时间最小的顶点。如:Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号stack 存储该连通子图的所有点。
当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下tarjan(u)
{
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u]= min(Low[u], Low[v])//记录最小顶点
else if (v in S) // 如果节点v还在栈内
Low[u]= min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
repeat
v = S.pop // 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}
3.算法流程的演示
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
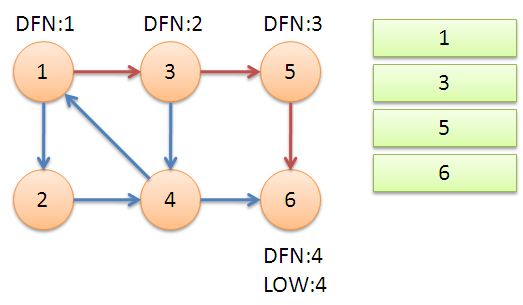
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
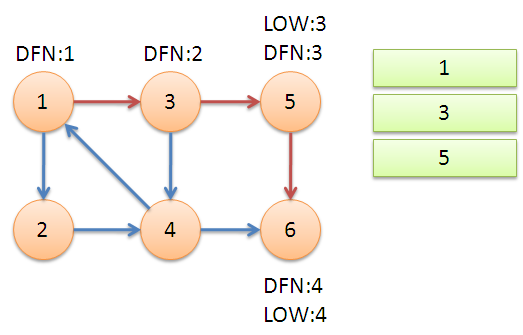
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。

继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
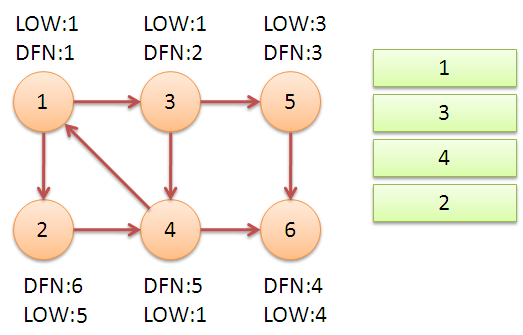
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
Tarjan算法:每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
参考博客:
HDU 1269 (模板题):
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define inf 0x3f3f3f3f
#define ll long long
#define sscc ios::sync_with_stdio(false);
#define ms(a) memset(a,0,sizeof(a))
#define mss(a) memset(a,-1,sizeof(a))
#define msi(a) memset(a,inf,sizeof(a))
using namespace std;
const int M=1e5+6;
int pre[M],ten,ans;//链式前向星
int dfn[M],low[M],cens,vis[M];//tarjan
stack st;
struct A{
int y,next;
}tens[M];
int add(int x,int y)//加边{
tens[ten].y=y,tens[ten].next=pre[x],pre[x]=ten++;
}
void tarjan(int v){
dfn[v]=low[v]=cens++,vis[v]=1,st.push(v);//分配一个序号 ,并进栈,标记
for(int i=pre[v];~i;i=tens[i].next)//遍历v点出发的全部边
{
int u=tens[i].y;//v->u的u点
if(dfn[u]==0)//如果这个点没访问过
{
tarjan(u);//向下访问
low[v]=min(low[v],low[u]);//去v和u的最小序
}else if(vis[u])//如果访问过,那就取最小序
low[v]=min(low[v],dfn[u]);
}
if(dfn[v]==low[v])//将该连通子图回退
{
int nums=0,j;
do{
j=st.top();//取栈顶
st.pop();//出栈
vis[j]=0;//取消标记
nums++;//统计改强连通分量的点的数量
}while(j!=v);//直到栈顶是v为止(v会被拿出来)
ans=max(ans,nums);
}
}
int main(){
sscc;
int n,m;
while(cin>>n>>m&&(n+m))
{
mss(pre),ten=0,cens=1,ans=-inf;
ms(dfn),ms(low),ms(vis);
for(int i=0;i
{
int x,y;
cin>>x>>y;
add(x,y);
}
for(int i=1;i<=n;i++)//防止有点不连通
{
if(!dfn[i])
tarjan(i);
}
if(ans==n)
cout<
else
cout<
}
return 0;
}