Canny边缘检测原理及其python实现
转载请注明出处:©️
Sylvan Ding
Canny边缘检测算法
多数分割算法均基于灰度值的两个基本性质之一:不连续性和相似性。图像的边缘检测就是基于灰度的不连续性(灰度突变)来实现图像分割的。
边缘检测器是设计用来检测边缘像素的局部图像处理方法。一条线可视为一条边缘线段,该线两侧的背景灰度要么远亮于该线像素的灰度,要么远暗于该线像素的灰度,这样的线称之为“屋顶边缘”。
虽然Canny[1968]算法复杂,但其边缘检测的表现却相当优秀。
工具介绍
为了方便计算,我们将所有灰度都标定到 [0,1](归一化),这样就无需考虑系数的问题了。
二阶偏微分
∂
f
∂
x
=
f
(
x
+
1
)
−
f
(
x
)
\frac{\partial f}{\partial x}=f(x+1)-f(x)
∂
x
∂
f
=
f
(
x
+
1
)
−
f
(
x
)
∂
2
f
∂
x
2
=
f
(
x
+
1
)
+
f
(
x
−
1
)
−
2
f
(
x
)
\frac{\partial^{2} f}{\partial x^{2}}=f(x+1)+f(x-1)-2 f(x)
∂
x
2
∂
2
f
=
f
(
x
+
1
)
+
f
(
x
−
1
)
−
2
f
(
x
)
在
实验3: 拉普拉斯锐化
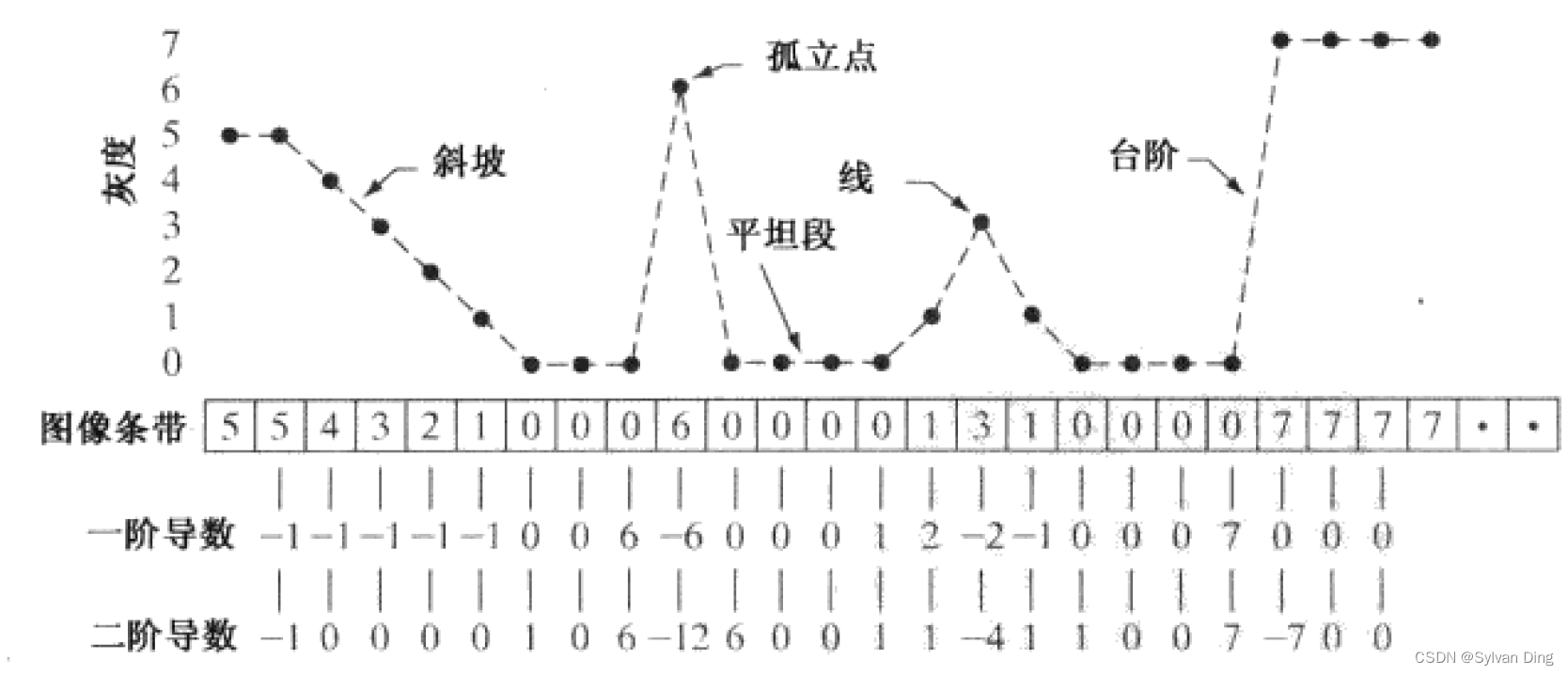
中曾讨论过用差分定义的导数来表征和检测灰度的突变,同时得到了如下结论:
- 二阶导数仅在“灰度斜坡”的开始、结尾处不为零,一阶导数在整个“灰度斜坡”上均不为零,因此一阶导数产生的边缘粗于二阶导数
- 同时,二阶导数变化的激烈度明显高于一阶导数,因此二阶导数更能增强细节(包括噪声、孤立点、边缘等)
- 在“斜坡”和“台阶”边缘二阶导数的符号相反,导致了“双边缘效应”,也可用于确定边缘是从亮到暗过渡还是从暗到亮过渡
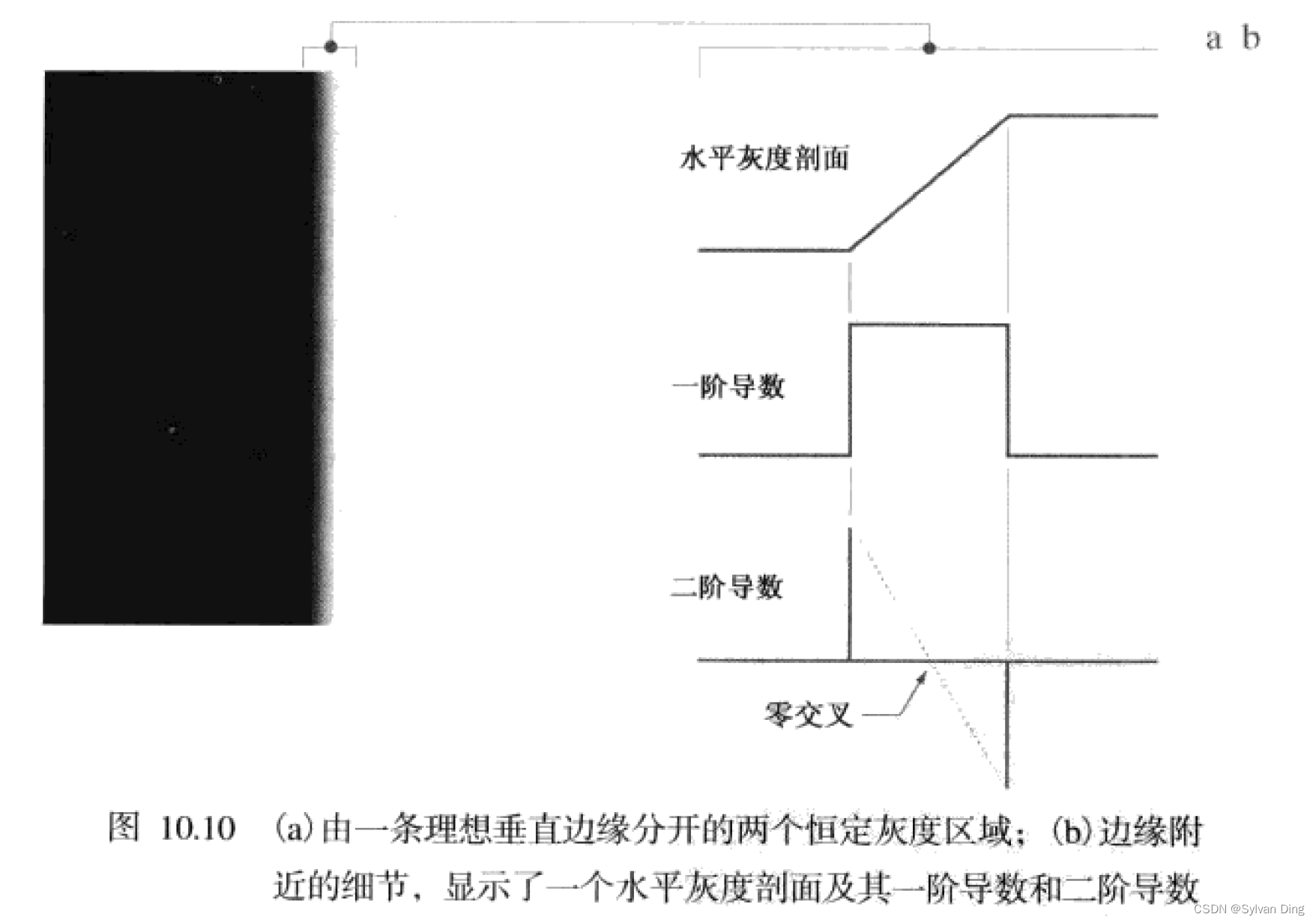
对于一条边缘来说,二阶导数具有如下性质:
- 对图像中的边缘,二阶导数生成两个值(双边缘效应)
- 二阶导数的零交叉点可用于定位粗边缘中心
高斯低通滤波
不难证明,微弱的可见噪声会对边缘检测的上述两个关键导数产生严重影响,特别是对二阶偏导数的影响非常剧烈。所以在执行边缘检测前,需要对图像进行平滑处理(降噪)。
高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,广泛应用于图像处理的减噪过程。通俗的讲,高斯滤波就是对整幅图像进行加权平均的过程,每一个像素点的值,都由其本身和邻域内的其他像素值经过加权平均后得到。
二维高斯函数(
μ
=
0
\mu=0
μ
=
0
, 中心点为原点)的定义如下:
G
(
x
,
y
)
=
e
−
x
2
+
y
2
2
σ
2
G(x, y)=\mathrm{e}^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}}
G
(
x
,
y
)
=
e
−
2
σ
2
x
2
+
y
2
注:
G(
x
,
y
)
G(x,y)
G
(
x
,
y
)
的系数
12
π
σ
2
\frac{1}{2\pi\sigma^2}
2
π
σ
2
1
可忽略,因为在计算得到权重矩阵后,还要对这个矩阵进行归一化。
用
G
G
G
和输入图像
f
f
f
卷积形成平滑后的图像
f
s
f_s
f
s
:
f
s
(
x
,
y
)
=
G
(
x
,
y
)
∗
f
(
x
,
y
)
f_s(x,y)=G(x,y)\ast f(x,y)
f
s
(
x
,
y
)
=
G
(
x
,
y
)
∗
f
(
x
,
y
)
梯度和梯度方向
为了在
f
f
f
中寻找边缘的强度和方向,所以引入梯度
∇
f
\nabla f
∇
f
,定义如下:
∇
f
≡
grad
(
f
)
≡
[
g
x
g
y
]
=
[
∂
f
∂
x
∂
f
∂
y
]
\nabla f \equiv \operatorname{grad}(f) \equiv\left[\begin{array}{l} g_{x} \\ g_{y} \end{array}\right]=\left[\begin{array}{l} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{array}\right]
∇
f
≡
g
r
a
d
(
f
)
≡
[
g
x
g
y
]
=
[
∂
x
∂
f
∂
y
∂
f
]
∇
f
\nabla f
∇
f
表征了
f
f
f
在该点
(
x
,
y
)
(x,y)
(
x
,
y
)
处最大变化率方向,其大小用
M
M
M
表示,方向角用
α
\alpha
α
表示(方向角是与以左上角为原点的坐标轴 x 轴之间的夹角):
M
(
x
,
y
)
=
g
x
2
+
g
y
2
M(x, y)=\sqrt{g_{x}^{2}+g_{y}^{2}}
M
(
x
,
y
)
=
g
x
2
+
g
y
2
α
(
x
,
y
)
=
arctan
[
g
y
g
x
]
\alpha(x, y)=\arctan \left[\frac{g_{y}}{g_{x}}\right]
α
(
x
,
y
)
=
arctan
[
g
x
g
y
]
M
(
x
,
y
)
M(x,y)
M
(
x
,
y
)
、
α
(
x
,
y
)
\alpha (x,y)
α
(
x
,
y
)
和
f
f
f
的尺寸相同,
∇
f
\nabla f
∇
f
和该点处的边缘正交,故梯度向量也称边缘法线。
通过
M
(
x
,
y
)
M(x,y)
M
(
x
,
y
)
和
α
(
x
,
y
)
\alpha (x,y)
α
(
x
,
y
)
,可以分别构造梯度幅值矩阵和方向矩阵。梯度幅值矩阵是梯度的大小,表征了边缘的强度。而梯度方向矩阵则表征了梯度的方向。但是在计算
M
(
x
,
y
)
M(x,y)
M
(
x
,
y
)
时,涉及平方和平方根操作,计算开销大,所以经常使用绝对值来近似梯度幅值:
M
(
x
,
y
)
≈
∣
g
x
∣
+
∣
g
y
∣
M(x, y) \approx\left|g_{x}\right|+\left|g_{y}\right|
M
(
x
,
y
)
≈
∣
g
x
∣
+
∣
g
y
∣
Sobel算子
梯度中偏导数
g
x
g_x
g
x
、
g
y
g_y
g
y
的计算需要使用模版(算子)对
f
f
f
进行滤波。
一维模版对x方向、y方向分别求偏导数,即求x方向、y方向的边缘,但未考虑对角线方向的偏导数。Roberts[1965]交叉梯度算子以求对角像素(
4
5
∘
,
−
4
5
∘
45^\circ,-45^\circ
4
5
∘
,
−
4
5
∘
)之差为基础,但
2
×
2
2\times 2
2
×
2
大小的模版对于用关于中心点对称的模版来计算边缘方向不是很有用,为了考虑中心点对称数据的性质、并携带有关边缘方向的更多信息,Prewitt[1970] 算子被提出:
P
r
e
w
i
t
t
x
=
[
−
1
−
1
−
1
0
0
0
1
1
1
]
,
P
r
e
w
i
t
t
y
=
[
−
1
0
1
−
1
0
1
−
1
0
1
]
Prewitt_x = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix}, Prewitt_y = \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}
P
r
e
w
i
t
t
x
=
⎣
⎡
−
1
0
1
−
1
0
1
−
1
0
1
⎦
⎤
,
P
r
e
w
i
t
t
y
=
⎣
⎡
−
1
−
1
−
1
0
0
0
1
1
1
⎦
⎤
索贝尔算子(Sobel operator)[1970]主要用作边缘检测,本质上是
一阶离散性差分算子
,用来计算图像亮度函数的偏导数的近似值,因为它可以反应出灰度值剧烈变化的区域,而平滑灰度值变化缓慢的区域。Sobel 算子在中心位置使用 2 以平滑图像,更好的抑制噪声,Sobel 算子如下:
S
o
b
e
l
x
=
[
−
1
−
2
−
1
0
0
0
1
2
1
]
,
S
o
b
e
l
y
=
[
−
1
0
1
−
2
0
2
−
1
0
1
]
Sobel_x = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}, Sobel_y = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}
S
o
b
e
l
x
=
⎣
⎡
−
1
0
1
−
2
0
2
−
1
0
1
⎦
⎤
,
S
o
b
e
l
y
=
⎣
⎡
−
1
−
2
−
1
0
0
0
1
2
1
⎦
⎤
那么,
G
x
=
S
o
b
e
l
x
∗
f
s
,
G
y
=
S
o
b
e
l
y
∗
f
s
G_x=Sobel_x\ast f_s\ ,\ G_y=Sobel_y\ast f_s
G
x
=
S
o
b
e
l
x
∗
f
s
,
G
y
=
S
o
b
e
l
y
∗
f
s
M
=
G
x
2
+
G
y
2
M=\sqrt{G_{x}^{2}+G_{y}^{2}}
M
=
G
x
2
+
G
y
2
α
=
arctan
[
G
y
G
x
]
\alpha=\arctan \left[\frac{G_{y}}{G_{x}}\right]
α
=
arctan
[
G
x
G
y
]
梯度阈值处理
为了减小噪声对梯度幅值矩阵的影响,即可以在计算梯度前,对图像进行低通滤波(平滑),也可以在计算梯度后,对梯度图像进行阈值处理,可以设置大于或等于梯度图像的最大值的 xx% 的像素显示为白色,而低于该阈值的像素则显示为黑色,以减小噪声的影响。但是,在阈值处理后,可能会导致部分边缘的断线。
Canny边缘检测核心思想
在Canny[1968]之前,Marr和Hildreth[1980]就用高斯拉普拉斯(LoG)函数生成模版来进行边缘检测,他们论证了滤波器
∇
2
G
\nabla ^2G
∇
2
G
的有效性。
Canny的三个目标:
- 低错误率。所有边缘都应被找到,并且没有伪响应;
- 边缘点被很好地定位。由检测器标记为边缘的点和真实边缘的中心之间的距离尽可能小;
- 单一的边缘点响应。对于真实的边缘点,检测器仅返回一个点,对于仅存一个单一边缘点的位置,检测器不应指出多个边缘像素
Canny基本步骤:
- 高斯滤波平滑输入图像
- 计算梯度幅值图像和角度图像
- 对梯度幅值图像应用非最大抑制(NMS)
- 双阈值处理,划分强、弱边缘
- 滞后边界跟踪,消除干扰(孤立弱边缘)
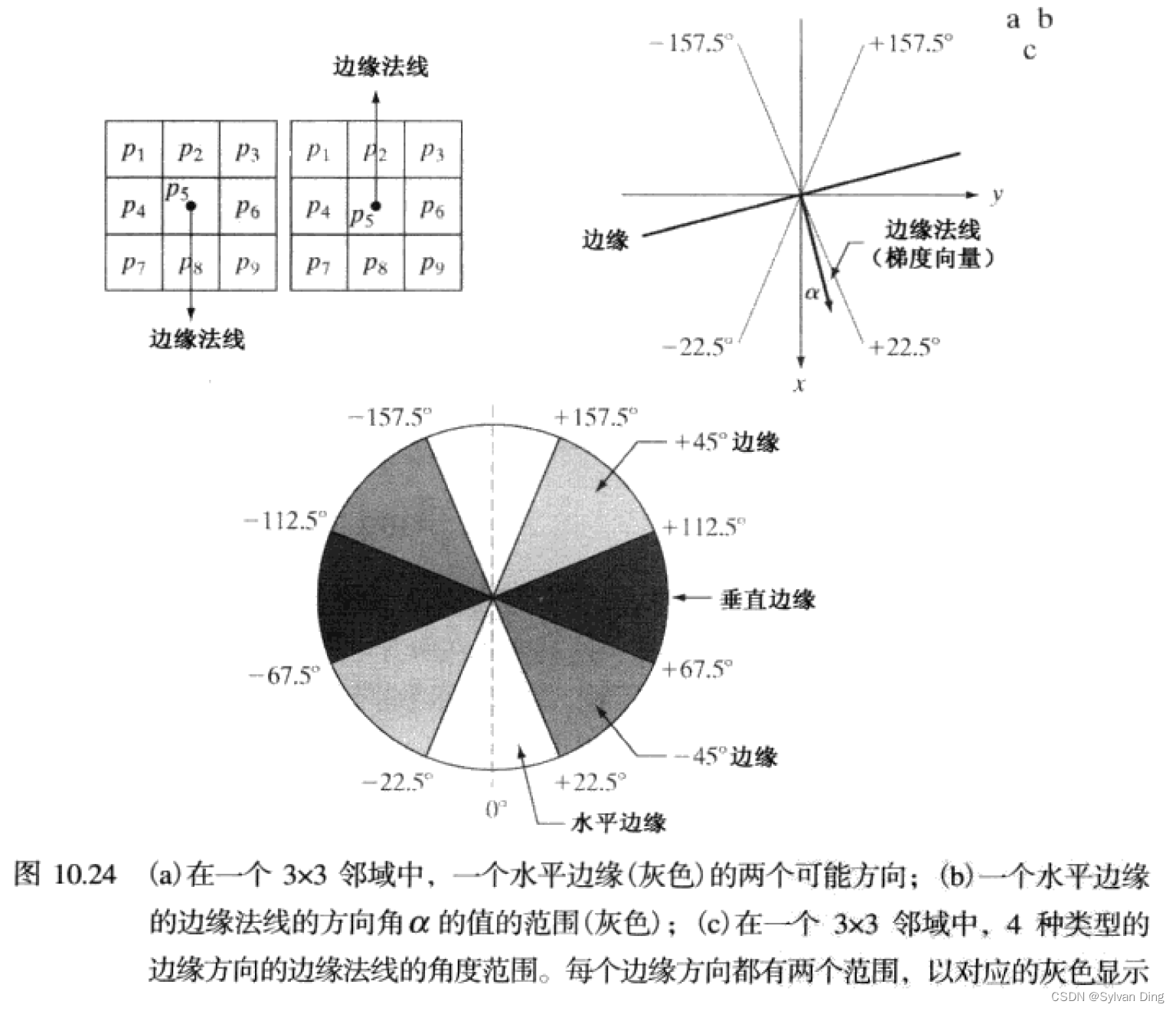
NMS
非最大值抑制(NMS)可以细化得到的边缘(梯度幅值),该方法本质上将边缘按梯度方向的范围进行离散化,定义了四个离散方向,分别是水平、垂直、
4
5
∘
45^\circ
4
5
∘
、
−
4
5
∘
-45^\circ
−
4
5
∘
. 以梯度幅值矩阵上每个点为中心,寻找其对于梯度方向最靠近的离散方向,若
M
(
x
,
y
)
M(x,y)
M
(
x
,
y
)
至少小于沿该方向的两个邻居之一,则抑制(
g
N
(
x
,
y
)
=
0
g_N(x,y)=0
g
N
(
x
,
y
)
=
0
),否则
g
N
(
x
,
y
)
=
M
(
x
,
y
)
g_N(x,y)=M(x,y)
g
N
(
x
,
y
)
=
M
(
x
,
y
)
.
NMS 的本质是对各点的由边缘法线确定的边缘进行细化,在该点处边缘的两侧和中心选取最大值,其余相邻像素位置零。
注意,查阅资料得知,NMS 也可以使用插值方法来精确计算,这里就用本书中提到的方法进行近似计算。
双阈值处理
最后对
g
N
g_N
g
N
进行双阈值处理,以减少伪边缘点(噪声)。
在用梯度幅值表征边缘时,用单阈值处理梯度幅值,若阈值过低,则会存在一些伪边缘,若阈值过高,则会删除有效边缘点,造成断线。
改进方式是设置两个阈值:
L
T
L_T
L
T
和
H
T
H_T
H
T
.
创建高、低阈值图像:
g
N
H
(
x
,
y
)
=
g
N
(
x
,
y
)
≥
T
H
g_{N H}(x, y)=g_{N}(x, y) \ge T_{H}
g
N
H
(
x
,
y
)
=
g
N
(
x
,
y
)
≥
T
H
g
N
L
(
x
,
y
)
=
g
N
(
x
,
y
)
≥
T
L
g_{N L}(x, y)=g_{N}(x, y) \geq T_{L}
g
N
L
(
x
,
y
)
=
g
N
(
x
,
y
)
≥
T
L
此时,
g
N
H
g_{N H}
g
N
H
中的所有非零像素都包含在
g
N
L
g_{N L}
g
N
L
中,则做如下运算得到“纯净的”
g
N
L
g_{N L}
g
N
L
(其像素点的灰度值在两阈值之间):
g
N
L
(
x
,
y
)
=
g
N
L
(
x
,
y
)
−
g
N
H
(
x
,
y
)
g_{N L}(x, y)=g_{N L}(x, y)-g_{N H}(x, y)
g
N
L
(
x
,
y
)
=
g
N
L
(
x
,
y
)
−
g
N
H
(
x
,
y
)
g
N
H
g_{N H}
g
N
H
中的所有强像素均被认定为有效边缘像素,立即标记。而由于
T
H
T_H
T
H
通常较大,故
g
N
H
g_{N H}
g
N
H
中的边缘会有缝隙。
滞后边界跟踪
弱边缘点则可能是真的边缘,也可能是噪声或颜色变化引起的。为得到精确的结果,后者引起的弱边缘点应该去掉。通常认为真实边缘引起的弱边缘点和强边缘点是连通的,而噪声引起的弱边缘点则不会。
滞后边界跟踪算法检查一个弱边缘点的 8 连通领域像素,只要有强边缘点存在,那么这个弱边缘点被认为是真是边缘保留下来。
这个算法搜索所有连通的弱边缘,如果一条连通的弱边缘的任何一个点和强边缘点连通,则保留这条弱边缘,否则抑制这条弱边缘。搜索时可以用广度优先或者深度优先算法。
算法说明如下:
-
输入:图像,计算其
gN
L
,
g
N
H
g_{NL},g_{NH}
g
N
L
,
g
N
H
-
建立
visited
矩阵(和输入图像同形),表征每个像素是否在 DFS 中被访问,初始化该矩阵为零矩阵 -
建立
gnl_filtered
矩阵,表征
gN
L
g_{NL}
g
N
L
中连通的弱边缘,且该弱边缘也和
gN
H
g_{NH}
g
N
H
中任意强边缘连通,即过滤调不符合条件的弱边缘后所剩下的符合条件的弱边缘(被认为是真边缘)。初始化该矩阵为零矩阵,不符合条件的弱边缘被抑制(置零) -
从上到下,自左向右,遍历所有强边缘
gN
H
g_{NH}
g
N
H
,若该像素已经被访问,则继续访问访问下一个像素,直到所有强边缘都被访问。若像素未被访问,进入 DFS. -
DFS 中,搜索该强边缘的连通弱边缘。先标记该点已被访问,如果该点的
gN
L
(
x
,
y
)
>
0
g_{NL}(x,y)\gt 0
g
N
L
(
x
,
y
)
>
0
,即该点是弱边缘,将
gnl_filtered
对应位置改为该点的灰度值(弱边缘符合条件保留),再一次递归搜索该点的8领域(寻找连通弱边缘)。DFS 的退出条件为已被标记(即
visited
矩阵对应位置为True)或访问的点超出边界。 - 输出:经过双阈值处理的强边缘矩阵、弱边缘矩阵,滞后边界跟踪的连通弱边缘矩阵
之后可对该灰度图像进行二值化并展示。
编码实现和结果分析
import cv2
import numpy as np
import matplotlib.pyplot as plt
img0 = 'house.tif'
f = cv2.imread(img0, cv2.IMREAD_GRAYSCALE)
plt.imshow(f, cmap='gray')
plt.show()

def gauss_seperate_kernel(kernel_size, sigma=1):
"""
create gaussian kernel use separable vector, because gaussian kernel is symmetric and separable.
param: kernel_size: input, the kernel size you want to create, normally is uneven number, such as 1, 3, 5, 7
param: sigma: input, sigma of the gaussian function, default is 1
return a desired size 2D gaussian kernel
"""
m = kernel_size[0]
n = kernel_size[1]
x_m = np.arange(m) - m // 2
y_m = np.exp(-(x_m ** 2) / (2 * sigma ** 2)).reshape(-1, 1)
x_n = np.arange(n) - n // 2
y_n = np.exp(-(x_n ** 2) / (2 * sigma ** 2)).reshape(-1, 1)
kernel = y_m * y_n.T
return kernel
n = 3 # gauss kernel size
sigma = 1 # sigma of the gaussian function
gauss_kernel = gauss_seperate_kernel((n, n), sigma=sigma)
fs = cv2.filter2D(f, ddepth=cv2.CV_32FC1, kernel=gauss_kernel, borderType=cv2.BORDER_DEFAULT)
plt.imshow(fs, cmap='gray')
plt.show()

sobelx = [[-1, -2, -1], [0, 0, 0], [1, 2, 1]]
sobelx = np.asarray(sobelx)
sobely = sobelx.T
Gx = cv2.filter2D(fs, -1, kernel=sobelx, borderType=cv2.BORDER_DEFAULT)
Gy = cv2.filter2D(fs, -1, kernel=sobely, borderType=cv2.BORDER_DEFAULT)
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].set_title('Gx')
axs[0].imshow(Gx, cmap='gray')
axs[1].set_title('Gy')
axs[1].imshow(Gy, cmap='gray')
plt.show()

很明显,
G
x
G_x
G
x
表征
x
x
x
方向上的边界,
G
y
G_y
G
y
表征
y
y
y
方向上的边界.
M = np.sqrt(np.square(Gx) + np.square(Gy))
alpha = np.arctan(np.divide(Gy, Gx, where=Gx!=0))
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].set_title('M')
axs[0].imshow(M, cmap='gray')
axs[1].set_title(r'\alpha')
axs[1].imshow(alpha, cmap='gray')
plt.show()
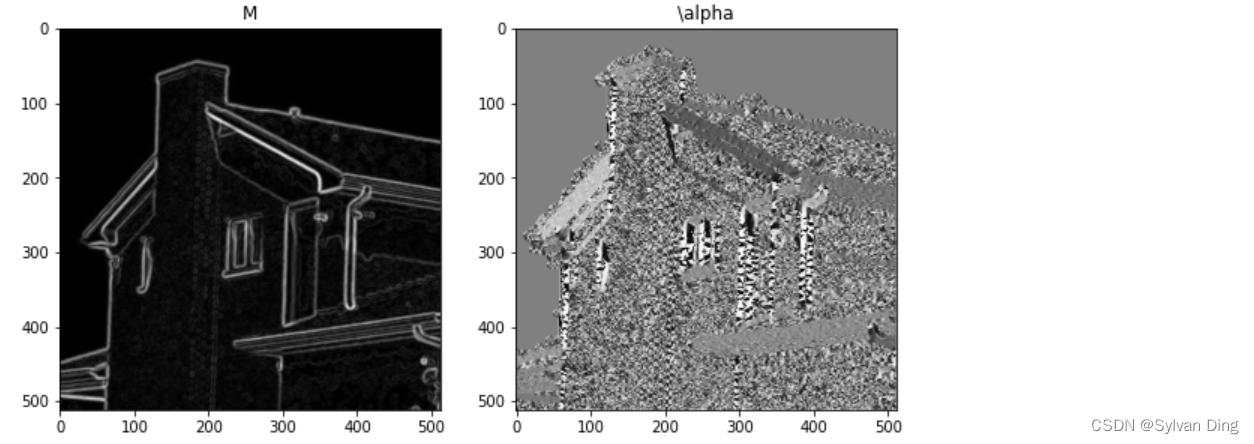
左图为梯度幅值,右图为梯度方向。
梯度幅值表征了边缘强度,梯度方向较好地识别了背景和房子,背景的梯度方向一致。
t = .33 # single threshold
Mt = M.copy()
Mt[Mt < t * np.max(Mt)] = np.min(Mt)
plt.imshow(Mt, cmap='gray')
plt.show()

可以看到,用单阈值直接处理梯度赋值图像得到的边缘中,一部分砖瓦的缝隙(我们不希望的)消失了,但也造成了部分边缘断线,且此时边缘仍然较粗。
def NMS(gradients, direction):
""" Non-maxima suppression
Args:
gradients: the gradients of each pixel
direction: the direction of the gradients of each pixel
Returns:
the output image
"""
W, H = gradients.shape
nms = np.copy(gradients)
for i in range(1, W - 1):
for j in range(1, H - 1):
theta = direction[i, j]
if np.abs(theta) < np.pi / 8:
d = [0, 1] # d1
elif np.abs(theta) > np.pi * 3 / 8:
d = [1, 0] # d3
elif np.pi / 8 <= theta:
d = [1, 1] # d2
else:
d = [1, -1] # d4
g1 = gradients[i + d[0], j + d[1]]
g2 = gradients[i - d[0], j - d[1]]
if g1 > gradients[i, j] or g2 > gradients[i, j]:
nms[i, j] = 0
return nms
Mn = NMS(M, alpha)
# binarization
Mn_b = np.copy(Mn)
threshold = 0.3 * np.max(Mn_b)
Mn_b[Mn_b < threshold] = 0
Mn_b[Mn_b >= threshold] = 1
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].set_title('Mn')
axs[0].imshow(Mn, cmap='gray')
axs[1].set_title('Mn_binarized')
axs[1].imshow(Mn_b, cmap='gray')
plt.show()
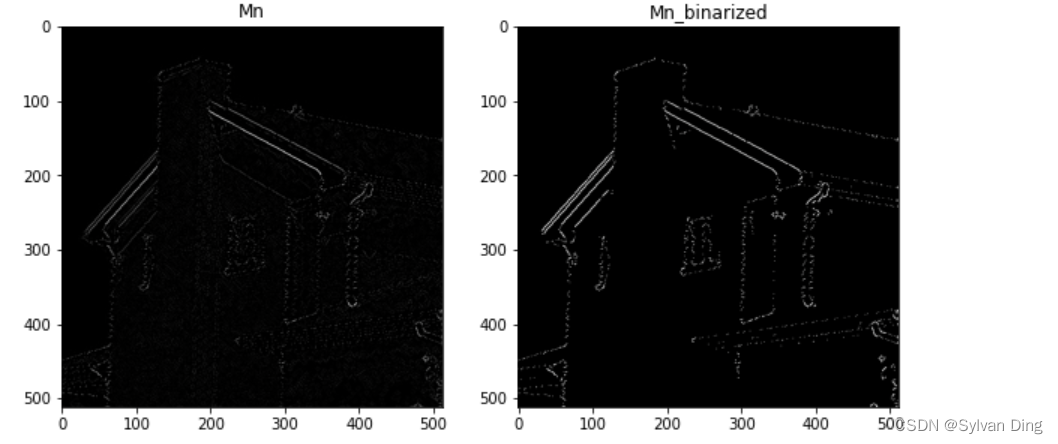
上图为经过 NMS 后的边缘梯度图像,边缘被细化了。接下来进行双阈值处理和滞后边缘跟踪,进一步细化边缘。
def double_threshold(gn, tl, th):
""" Double Threshold
Use two thresholds to compute the edge.
Args:
gn: the input image
tl: the low threshold
th: the high threshold
Returns:
gnh, gnl, and true_gnl
"""
gnh, gnl = np.copy(gn), np.copy(gn)
tl = np.max(gn) * tl
th = np.max(gn) * th
gnh[gnh < th] = .0
gnl[gnl < tl] = .0
gnl = gnl - gnh
visited = np.zeros_like(gn)
gnl_filtered = np.zeros_like(gn).astype('float')
W, H = gn.shape
def dfs(i, j):
if i >= W or i < 0 or j >= H or j < 0 or visited[i, j] == 1:
return
visited[i, j] = 1
if gnl[i, j] > 0 or gnh[i, j] > 0:
gnl_filtered[i, j] = gnl[i, j]
dfs(i - 1, j - 1)
dfs(i - 1, j)
dfs(i - 1, j + 1)
dfs(i, j - 1)
dfs(i, j + 1)
dfs(i + 1, j - 1)
dfs(i + 1, j)
dfs(i + 1, j + 1)
for w in range(W):
for h in range(H):
if visited[w, h] == 1:
continue
if gnh[w, h] > 0:
dfs(w, h)
return gnh, gnl, gnl_filtered
def draw_double_threshold(gn, tl, th):
"""
draw result pictures
:return: gNH_b+gNL_true_b
"""
gNH, gNL, gNL_true = double_threshold(gn=gn, tl=tl, th=th)
gNH_b = gNH.copy()
gNL_b = gNL.copy()
gNL_true_b = gNL_true.copy()
gNH_b[gNH_b > 0] = np.max(gNH_b)
gNL_b[gNL_b > 0] = np.max(gNL_b)
gNL_true_b[gNL_true_b > 0] = np.max(gNL_true_b)
combination = gNH_b + gNL_true_b
combination[combination > 0] = np.max(combination)
fig, axs = plt.subplots(2, 2, figsize=(10, 10))
axs[0][0].set_title('gNH_b')
axs[0][0].imshow(gNH_b, cmap='gray')
axs[0][1].set_title('gNL_b')
axs[0][1].imshow(gNL_b, cmap='gray')
axs[1][0].set_title('gNL_true_b')
axs[1][0].imshow(gNL_true_b, cmap='gray')
axs[1][1].set_title('combination: gNH_b+gNL_true_b')
axs[1][1].imshow(combination, cmap='gray')
plt.suptitle('tl={}, th={}'.format(tl, th))
plt.show()
return combination
tl0 = 0.05
th0 = 0.4
binarized_res0 = draw_double_threshold(Mn, tl0, th0)
tl1 = 0.1
th1 = 0.5
binarized_res1 = draw_double_threshold(Mn, tl1, th1)

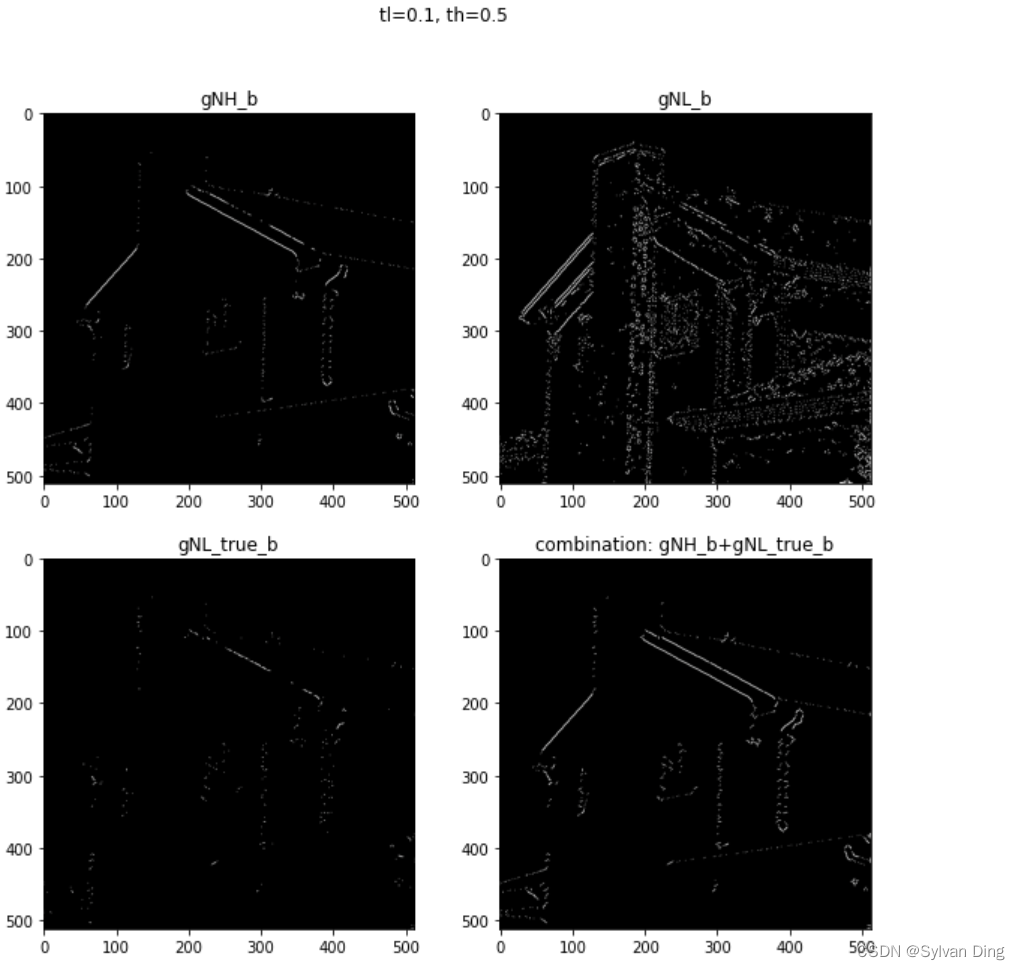
适当提高双阈值后(
(0.05, 0.4)->(0.1, 0.5)
),对噪声的过滤增强,对强边缘的要求提高,故强边缘像素减少、弱边缘中噪声也减少。
过滤弱边缘中非连通边缘,再将过滤后的弱边缘和强边缘二值化图相加,得到最终的二值化边缘结果
gNH_b+gNL_true_b
.
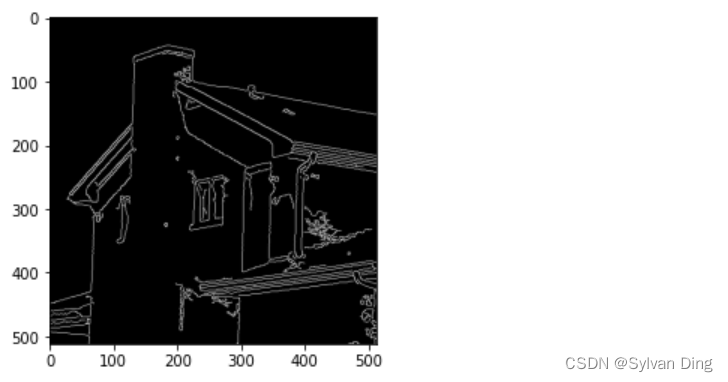
# 和cv2库Canny函数对比
tl2 = 255 * 0.1
th2 = 255 * 0.5
g = cv2.Canny(f, tl2, th2)
plt.imshow(g, cmap='gray')
plt.show()
参考文献
- 数字图像处理:第3版,北京:电子工业出版社
-
图像滤波之高斯滤波
-
边缘检测之Sobel检测算子
-
Canny边缘检测算法的python实现
-
常用测试数据集下载:“Standard” test images