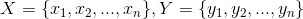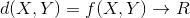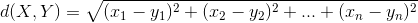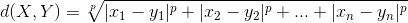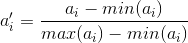码字不易，转发请注明出处：

http://blog.csdn.net/qq_28945021/article/details/51960232

摘要

MLlib（机器学习）分两种——监督学习，无监督学习。首先监督学习，类似普贝叶斯这样的分类算法。要求必须事先明确知道各个类别的信息，并且断言所有待分类项都有一个类别与之对应。显而眼见的是，这种需求另监督学习有很大的局限性，尤其在海量数据处理时。要预先处理数据以满足算法需求得耗费大量资源与时间。此时，可以使用聚类算法这样的无监督学习，相比于分类，聚类不依赖预定义的类和类标号的训练实例。本文将聚类算法拆分开来。深刻理解其思想。

相关知识

相异度计算——聚类，见名之意，便是将数据聚集起来，但是并非是将所有数据聚集到一个点。而是根据需要聚集成多个点。而聚到哪个点的依据。便是元素与中心的相异度。其实可以将聚类简单的理解为，通过相异度将数据划分开来。然后各自聚集在一起。

设

，其中X，Y是两个元素项，各自具有n个可度量特征属性，那么X和Y的相异度定义为：

，其中R为实数域。也就是说相异度是两个元素对实数域的一个映射，所映射的实数定量表示两个元素的相异度。

接下来说说一些常见类型的变量的相异度的计算方式：

标量

标量也就是无方向意义的数字，也叫标度变量。例如：X{1,2,3}，Y{2,3,4}。常用的计算方式是求其的

欧几里得距离

作为相异度。欧几里得距离定义如下：



其意义就是两个元素在欧氏空间中的集合距离，因为其直观易懂且可解释性强，被广泛用于标识两个标量元素的相异度。

还有比较常用的方式是曼哈顿距离和闵可夫斯基距离。

曼哈顿距离：

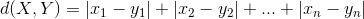
闵可夫斯基距离：


欧氏距离和曼哈顿距离可以看做是闵可夫斯基距离在p=2和p=1下的特例。实际上都十分容易理解。

虽说上述的算法计算能够计算相异度。但是不难看出，在类似x1和y1的差距过大时，会对相异度有很大的影响。比如X{101,2},Y{1，1}使用欧几里得距离计算后得到的相异度近似为100，这显然是不正常的。所以，在使用上述算法时，需要对数据进行规格化——

所谓规格化就是将各个属性值按比例映射到相同的取值区间，这样是为了平衡各个属性对距离的影响。通常将各个属性均映射到[0,1]区间，映射公式为：




其中max(ai)和min(ai)表示所有元素项中第i个属性的最大值和最小值。

二元变量

所谓二元变量其实就是是只能取0和1两种值变量，有点类似布尔值，通常用来标识是或不是这种二值属性。对于二元变量，一种常用的方法是用元素相同序位同值属性的比例来标识其相异度。

设有X={1,0,0,0,1,0,1,1}，Y={0,0,0,1,1,1,1,1}，可以看到，两个元素第2、3、5、7和8个属性取值相同，而第1、4和6个取值不同，那么相异度可以标识为3/8=0.375。一般的，对于二元变量，相异度可用“

取值不同的同位属性数/单个元素的属性位数

”标识。

上面所说的相异度应该叫做对称二元相异度。现实中还有一种情况，就是我们只关心两者都取1的情况，而认为两者都取0的属性并不意味着两者更相似。例如在根据病情对病人聚类时，如果两个人都患有肺癌，我们认为两个人增强了相似度，但如果两个人都没患肺癌，并不觉得这加强了两人的相似性，在这种情况下，改用“

取值不同的同位属性数/(单个元素的属性位数-同取0的位数)

”来标识相异度，这叫做非对称二元相异度。如果用1减去非对称二元相异度，则得到非对称二元相似度，也叫Jaccard系数，是一个非常重要的概念。

分类变量

分类变量是二元变量的推广，类似于程序中的枚举变量，但各个值没有数字或序数意义，如颜色、民族等等，对于分类变量，用“取值不同的同位属性数/单个元素的全部属性数”来标识其相异度。

序数变量

序数变量是具有序数意义的分类变量，通常可以按照一定顺序意义排列，如冠军、亚军和季军。对于序数变量，一般为每个值分配一个数，叫做这个值的秩，然后以秩代替原值当做标量属性计算相异度。

聚类

所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。

Kmeans算法

算法流程

K-means是一个反复迭代的过程，算法分为四个步骤：

1） 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；

2） 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；

3） 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；

4） 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）。

其实理解起来还是十分容易的：由于刚开始处理数据，对数据的信息并不是十分了解，所以开始需要随机取中心（k值根据现实需求定），而聚类的精髓在于根据相异度进行数据划分。因此在选取中心点后，便是计算整个样本中的所有数据对象与中心点的相异度进行数据划分。

第一次数据划分完毕。这是的聚类由于中心是随机挑选的。因为并非十分准确。这时，求出该簇中的数据对象的算术平均值作为中心点。重新计算相异度。能够有效地减少误差。递归 这段操作，直到簇不变时，自然便是算法收敛。

如下例子是在借鉴别人的，还是十分明确的。

原文地址：

http://www.cnblogs.com/ybjourney/p/4714870.html

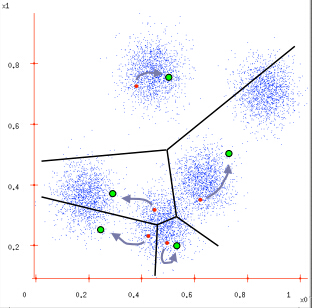
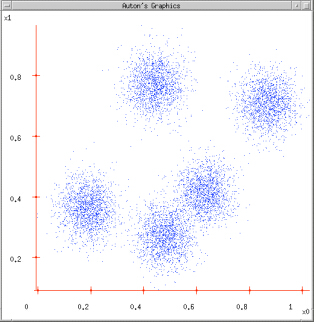
图1：给定一个数据集；

图2：根据K = 5初始化聚类中心，保证　聚类中心处于数据空间内；

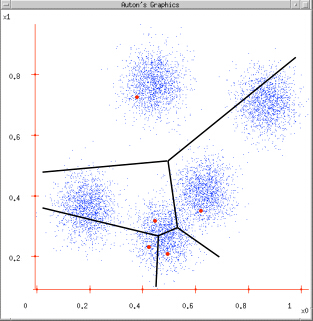
图3：根据计算类内对象和聚类中心之间的相似度指标，将数据进行划分；

图4：将类内之间数据的均值作为聚类中心，更新聚类中心。

最后判断算法结束与否即可，目的是为了保证算法的收敛。