1. 分别用Gauss消去法、列主元Gauss消去法、三角分解方法求解方程组
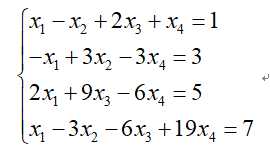
程序:
(1)Guess消去法:
function x=GaussXQByOrder(A,b)
%Gauss消去法
N = size(A);
n = N(1);
x = zeros(n,1);
for i=1:(n-1)
for j=(i+1):n
if(A(i,i)==0)
disp(‘对角元不能为0‘);
return;
end
m = A(j,i)/A(i,i);
A(j,i:n)=A(j,i:n)-m*A(i,i:n);
b(j)=b(j)-m*b(i);
end
end
x(n)=b(n)/A(n,n);
for i=n-1:-1:1
x(i)=(b(i)-sum(A(i,i+1:n)*x(i+1:n)))/A(i,i);
end
命令行输入:
A=[1 -1 2 1;-1 3 0 -3 ;2 0 9 -6;1 -3 -6 19];
b=[1 3 5 7];
b=b‘;
x=GaussXQByOrder(A,b)
运算结果:
x =
-8.000000000000000
0.333333333333333
3.666666666666667
2.000000000000000
(2)列主元Gauss消去法
程序:
function x=GaussXQLineMain(A,b)
%列主元Gauss消去法
N = size(A);
n = N(1);
x = zeros(n,1);
zz=zeros(1,n);
for i=1:(n-1)
[~,p]=max(abs(A(i:n,i)));
zz=A(i,:);
A(i,:)=A(p+i-1,:);
A(p+i-1,:)=zz;
temp=b(i);
b(i)=b(i+p-1);
b(i+p-1)=temp;
for j=(i+1):n
m = A(j,i)/A(i,i);
A(j,i:n)=A(j,i:n)-m*A(i,i:n);
b(j)=b(j)-m*b(i);
end
end
x(n)=b(n)/A(n,n);
for i=n-1:-1:1
x(i)=(b(i)-sum(A(i,i+1:n)*x(i+1:n)))/A(i,i);
end
命令行:
A=[1 -1 2 1;-1 3 0 -3 ;2 0 9 -6;1 -3 -6 19];
b=[1 3 5 7];
b=b‘;
x=GaussXQLineMain(A,b)
运行结果:
x =
-8.000000000000005
0.333333333333332
3.666666666666668
2.000000000000000
(3)三角分解方法
程序:
function x = LU(A,b)
%三角分解
N = size(A);
n = N(1);
L = eye(n,n);
U = zeros(n,n);
x = zeros(n,1);
y = zeros(n,1);
U(1,1:n) = A(1,1:n);
L(1:n,1) = A(1:n,1)/U(1,1);
for k=2:n
for i=k:n
U(k,i) = A(k,i)-L(k,1:(k-1))*U(1:(k-1),i);
end
for j=(k+1):n
L(j,k) = (A(j,k)-L(j,1:(k-1))*U(1:(k-1),k))/U(k,k);
end
end
y(1)=b(1)/L(1,1);
for i=2:n
y(i)=b(i)-sum(L(i,1:i-1)*y(1:i-1));
end
x(n)=y(n)/U(n,n);
for i=n-1:-1:1
x(i)=(y(i)-sum(U(i,i+1:n)*x(i+1:n)))/U(i,i);
end
命令行:
A=[1 -1 2 1;-1 3 0 -3 ;2 0 9 -6;1 -3 -6 19];
b=[1 3 5 7];
b=b‘;
x=LU(A,b)
运行结果:
x =
-8.000000000000000
0.333333333333333
3.666666666666667
2.000000000000000

程序:function [times,wucha]=zhuiganfa(a,b,c,f)
%追赶法:x为所求解,times为所有乘除运算次数(即时间),wucha为误差的2-范数。
n=length(f);
x=zeros(n,1);
y=zeros(n,1);
times=0;
alpha=zeros(1,n);
p=zeros(1,n-1);
alpha(1)=b(1);
for i=2:n
p(i-1)=c(i-1)/alpha(i-1);
alpha(i)=b(i)-a(i-1)*p(i-1);
times=times+1;
end
y(1)=f(1)/b(1);
for i=2:n
y(i)=(f(i)-a(i-1)*y(i-1))/alpha(i);
times=times+1;
end
x(n)=y(n);
for i=n-1:-1:1
x(i)=y(i)-p(i)*x(i+1);
times=times+1;
end
A=zeros(n,n);
A=diag(b,0)+diag(a,-1)+diag(c,1);
wucha=norm((A*x-f‘),2);
命令行(n=20):
a=repmat(11,1,19);
b=repmat(-19,1,20);
c=repmat(7,1,19);
f1=repmat(1.1,1,18);
f=[0 f1 1];
[times,wucha]=zhuiganfa(a,b,c,f)
运行结果:
times =
57
wucha =
8.009010697694412e-15
n=50时
命令行:
a=repmat(11,1,49);
b=repmat(-19,1,50);
c=repmat(7,1,49);
f1=repmat(1.1,1,48);
f=[0 f1 1];
[times,wucha]=zhuiganfa(a,b,c,f)
运行结果:
times =
147
wucha =
1.292635294609912e-14
命令行(n=100)
a=repmat(11,1,99);
b=repmat(-19,1,100);
c=repmat(7,1,99);
f1=repmat(1.1,1,98);
f=[0 f1 1];
[times,wucha]=zhuiganfa(a,b,c,f)
结果:
times =
297
wucha =
2.599344850768740e-14

程序:function [count,wucha] = zhouqisanduijaiozhuiganfa(a,b,c,f)
%x为所求解,count为所有乘除运算次数
n=length(f);
x=zeros(n,1);
y=zeros(n,1);
count=0;
l=zeros(1,n-2);
s=zeros(1,n-1);
u=zeros(1,n);
t=zeros(1,n-1);
u(1)=b(1);t(1)=1;
s(1)=1/u(1);y(1)=f(1);
for i=2:n-1
l(i-1)=a(i-1)/u(i-1);
u(i)=b(i)-l(i-1)*c(i-1);
t(i)=-l(i-1)*t(i-1);
s(i)=-s(i-1)*c(i-1)/u(i);
y(i)=f(i)-l(i-1)*y(i-1);
count=count+4;
end
st=0;
for k=1:n-1
st=st+s(k)*t(k);
count=count+1;
end
sy=0;
for k=1:n-2
sy=sy+s(k)*y(k);
count=count+1;
end
u(n)=b(n)-st-s(n-1)*(c(n-1)+t(n-1));
y(n)=f(n)-sy;
x(n)=y(n)/u(n);
for i=n-1:-1:1
x(i)=(y(i)-c(i)*x(i+1)-t(i)*x(n))/u(i);
count=count+1;
end
A=zeros(n,n);
A=diag(b,0)+diag(a,-1)+diag(c,1);
A(n,1)=1;
A(1,n)=1;
wucha=norm((A*x-f‘),2);
命令行:
n=10;
a=repmat(11,1,n-1);b=repmat(-19,1,n);
c=repmat(7,1,n-1);f1=repmat(1.1,1,n-2);f=[0 f1 1];
[count,wucha]= zhouqisanduijaiozhuiganfa(a,b,c,f)
运行结果:
count =
58
wucha =
4.525439045433075
n=30
count =
198
wucha =
5.951269557941316
n=100
count =
688
wucha =
5.993271932634396