第四章:树与二叉树(二叉树的逻辑结构)
1.二叉树
二叉树是树结构的一种,故二叉树也是逻辑结构。
二叉树
:二叉树是n(n≥0)个结点的有限集合。
- 1)n=0时,二叉树为空;
- 2)n>0时,由根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树也分别是一棵二叉树。
五种基本形态
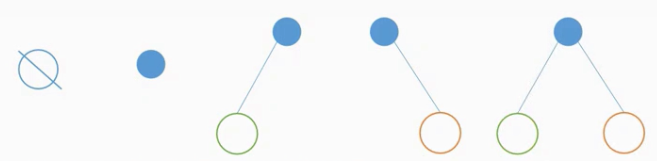
三个结点的二叉树有多少种??
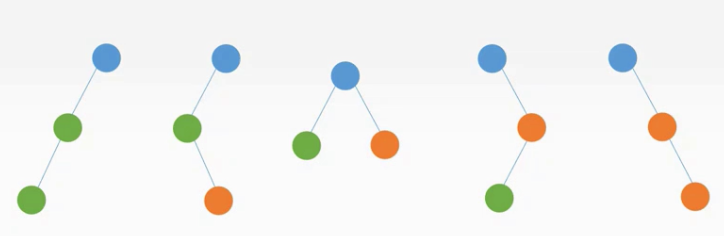
2.二叉树VS度为2的有序树
- 1)二叉树可以为空,而度为2的有序树至少有三个结点
度为2的有序树,则说明必须有一个结点的子节点为两个
- 2)二叉树的孩子结点始终有左右之分,而度为2有序树的孩子结点次序是相对的
在度为2的有序树中,如果有一个结点只有一个孩子结点,则是不分左右的。
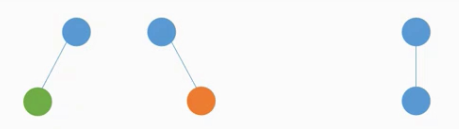
3.特殊二叉树
3.1满二叉树
满二叉树
:一棵高度为h,且含有2^h-1个结点的二叉树为满二叉树。
上篇文章中讲树的时候我们知道:高度为h的m叉树至多有(m^h-1)/(m-1) 个结点。这里我们把m换成2,即可。

编号规则
:从上到下、从左到右;
观察上述编号可以发现下面结论:
对于编号为
i
的结点,若存在,其双亲的编号为(
i/2
取整),左孩子为
2i,
右孩子为
2i+1
3.2完全二叉树
完全二叉树
:设一个高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号1~n的结点
一 一
对应时,称为完全二叉树。


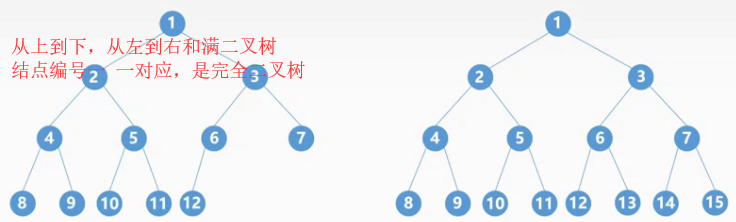
我们可以发现,如果一个二叉树是完全二叉树,则此二叉树除了最后一层结点数不满外,其余层结点数都是满的。
完全二叉树的性质
:
- 若 i <= n/2 取整数,则结点 i 为分支结点,否则为叶子结点。
i
是结点编号,
n
是结点的总数。
- 叶子结点只可能在层次最大的两层上出现。对于最大层次的叶子结点,都依次排在最左边的位置上。
- 度为1的结点若存在,则可能只有一个,且是编号最大的分支结点,并且孩子结点一定是左结点。
因为完全二叉树的编号是按照从上到下,从左到右编号的,而且除了最后一层结点数不满外,其余层结点数都是满的,所以度为1的结点可能存在也可能不存在,如果存在只可能在最后一个结点的双亲结点才能出现度为1的结点。
所有的性质都紧紧依赖完全二叉树的编号是从上到下,从左到右的。
3.3二叉排序树
二叉排序树
:一棵二叉树,若树非空则具有如下性质:
- 对任意结点若存在左子树或右子树,则其左子树上所有结点的关键字均小于该结点。
- 右子树上所有结点的关键字均大于该结点。
可以发现二叉排序树的左子树和右子树都是一棵二叉排序树。
3.4平衡二叉树
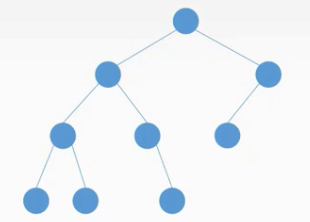
平衡二叉树
:树上
任意结点
的
左子树
和
右子树
的深度差不超过1
f复习:高度和深度的定义,某节点的
深度
是指从根节点到该节点的最长简单路径边的条数,而高度是指从该节点到叶子节点的最长简单路径边的条数。记住:深度是从根结点到该结点的边数的,而高度是从叶子节点往上数到该结点的边数。
注意:这里边的条数是规定根节点的深度和叶子节点的高度是0;
所以树的深度和高度是相等的,而对其他节点来说深度和高度不一定相等。

上图就不是一个平衡二叉树:
上图根结点的左子树深度为3,右子树深度为2,3-2=1,没问题,但是A结点的左子树深度为2,而A结点的右子树深度为0,2-0=2>1,不对。
4.二叉树的性质
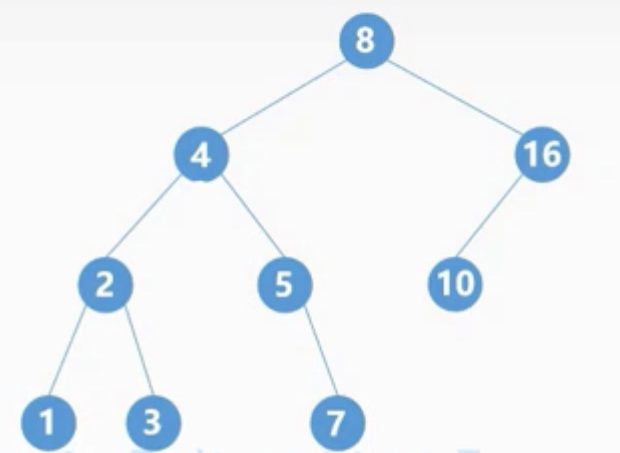
4.1n0=n2+1
-
非空二叉树上的叶子结点数等于度为2的结点数加1,即
n0=n2+1
.

如图上述二叉树:
-
首先我们知道二叉树的结点数等于各种度数二叉树结点的和,即
n=n0+n1+n2
。 -
另外
n=0*n0+1*n1+2*n2+1
,这个计算方法是按照子节点个数计算的,
0*n0
代表叶子节点的子节点数(叶子结点子节点数为0,故乘以0),
1*n1
代表子节点数为1的结点的个数,
2*n2
代表子节点数为2的结点的个数,最后加上1,代表根结点。
将上面的两个关于n的式子相减即可得到:
n0=n2+1
4.2性质2
非空二叉树上第 k 层上至多有 2^(k-1)个结点(k≥1)

4.3性质3
高度为h的二叉树至多有2^h -1个结点(h>=1) [满二叉树结点的总数]
4.4性质4
4)对完全二叉树按从上到下、从左到右的顺序依次编号1,2,…n,则有以下关系:
- 当 i>1 时,结点的双亲结点标号为 i/2 取整数, 即当 i 为偶数时,其双亲结点的编号为 i/2 ,他是双亲结点的左孩子;当为奇数时,其双亲结点的编号为(i-1)/2, 他是双亲结点的右孩子。
- 当 2i <= n 时,结点 i 的左孩子编号为 2i ,否则无左孩子
- 当 2i+1<=n 时,结点 i 的右孩子编号为 2i+1,否则无右孩子

4.5性质5
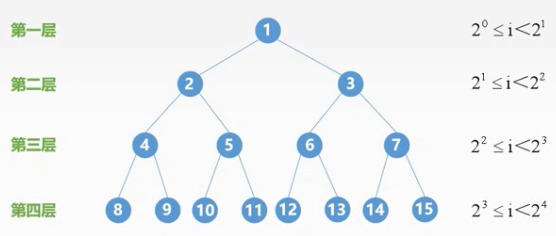
则第h层,
2^(h-1) =< i < 2^h
,对该式子两端取对数,则
h-1 =< log2i< h
,我们对log2i取下界,则得到h-1,再加1则得到系欸但所在的层次:
[log2i] +1
4.6性质6

由性质3:高度为h的二叉树至多有
2^h -1
个结点(h>=1)。令
2^h -1=n
,则可以推出 h = log2(n+1),至于这里为啥要取上界,是因为这个性质3,是按照满二叉树情况,但是完全二叉树的最后一层结点数不一定能达到最多,但也要算一层。
关于数据结构的知识,持续更新中,欢迎关注公众号
理木客
