-
空间向量的基本概念
1.空间向量的概念:
定义:
在空间,我们把具有大小和方向的量叫做向量。
模长:
向量的大小叫做向量的模,
a
的模长记作│
a
│
备注:
文中加粗的小写字母均代表向量。
2.空间向量的运算:
运算法则:
与平面向量运算一样,空间向量的加法、减法符合三角形法则跟平行四边形法则
运算率:
加法交换律:
a
+
b
=
b
+
a
加法结合律:(
a
+
b
)+
c
=
a
+(
b
+
c
)
数乘分配率:λ(
a
+
b
)= λ
a
+λ
b
3.共线向量:
定义:
如果表示空间向量的有向线段所在的直线平行或者重合,那么这些向量也叫共线向量或者平行向量
共线向量定理:
空间任意两个向量
a
,
b
,且
a
≠
0
,
a
∥
b,
存在实数λ,使
b
=λ
a
三点共线:
此部分的内容与平面向量的三点共线是一致的,A,B,C三点共线能得到以下两个等式。

4.共面向量:
定义:
一般地,能平移到同一平面内的向量叫做共面向量
备注:
空间内任意的两个向量肯定是共面的,因为向量可以进行平移
共面向量定理:
如果两个向量
a
,
b
不共线,
p
与向量
a
,
b
共面的条件是存在实数x,y使
p
=x
a
+y
b
四点共面:
若A,B,C,D四点共面也可以得到以下两个等式

5.空间向量基本定理:
定理:
如果三个向量
a
,
b
,
c
不共面,那么对空间任一向量
p
,存在一个唯一的有序实数组x,y,z,使
p
=x
a
+y
b
+z
c
备注:
若三向量
a
,
b
,
c
不共面,我们把{
a
,
b
,
c
}叫做空间的一个基底,
a
,
b
,
c
叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。
推论:
设O,A,B,C是不共面的四点,则对空间任一点P,都存在唯一的三个有序实数x,y,z,使:
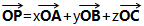
6.空间向量的数量积:
向量的数量积:
此部分内容也与平面向量相同,
a
·
b
=│
a
│·│
b
│·cos<
a
,
b
>
备注:
① a
2=│
a
│2
② 0
向量与任何向量的数量积均为0
空间向量数量积运算率:
(λ
a
)
b
=λ(
a·b
)=
a
(λ
b
)
a
·
b
=
b
·
a
a·(b
+
c)
=
a·b
+
a·c
7.空间向量的直角坐标系:
空间直角坐标系:
在空间直角坐标系O-xyz中,对空间任一点A,存在唯一的有序实数组(x,y,z),使OA=x
i
+y
j
+z
k
,有序实数组(x,y,z)叫作向量A在空间直角坐标系O-xyz中的坐标,记作A(x,y,z),x叫横坐标,y叫纵坐标,z叫竖坐标。
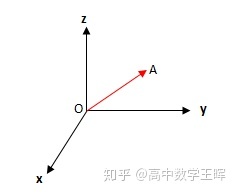
备注:
向量
i
,
j
,
k
作为空间直角坐标系的基底,是三个互相垂直的向量,长度为1,这样的基底叫单位正交基底。
建立空间直角坐标系的右手定则:
伸出右手的大拇指、食指和中指,并互为90°,则大拇指代表X坐标,食指代表Y坐标,中指代表Z坐标;大拇指的指向为X坐标正方向,食指的指向为Y坐标的正方向,中指的指向为Z坐标的正方向。
空间向量的坐标运算:
a
=(x1,y1,z1),
b
=( x2,y2,z2)
a
+
b
=(x1+x2,y1+y2,z1+z2)
a
–
b
=(x1-x2,y1-y2,z1-z2)
λ
a=
( λx1,λy1,λz1)
a
·
b=
x1x2+y1y2+z1z2
a∥b:
x1
=
λx2,y1=λy2,z1=λz2
a
⊥
b
:x1x2+y1y2+z1z2=0

-
立体几何在空间向量中的应用
1.法相量
定义:
如果表示向量
n
的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作
n
⊥α,那么向量
n
叫做平面α的法向量.
注意:
①
法向量一定是非零向量;
②
一个平面的法向量不唯一,但所有的法向量都互相平行;
③
向量
n
是平面的法向量,向量
m
是与平面平行或在平面内,则有
n
·
m
=0
求平面法相量的步骤:
①
设一个平面的法向量为
n
=(x,y,z)
②
找出平面内两个不共线的向量,并求出其坐标
a
=(a1,b1,c1)和
b
=(a2,b2,c2)
③
根据法相量的定义建立方程组

④
解方程组,求出其中的一个解,即得到法向量
2.用向量法解决立体几何平行问题
设直线L,m的方向向量分别是
a
,
b
,平面α,β的法向量分别是
n1
,
n2
线线平行:
L∥m⇔
a
∥
b
⇔
a
=k
·b
线面平行:
L∥α⇔
a⊥n1
⇔
a·n1
=0
面面平行:
α∥β⇔
n1
∥
n2
⇔
n1
=k
·n2
3.用向量法解决立体几何垂直问题
设直线L,m的方向向量分别是
a
,
b
,平面α,β的法向量分别是
n1
,
n2
线线垂直:
L⊥m⇔
a
⊥
b
⇔
a·b
=0
线面垂直:
L⊥α⇔
a
∥
n1
⇔
a
=k
·n1
面面垂直:
α⊥β⇔
n1
⊥
n2
⇔
n1·n2
=0
4.用向量法解决立体几何空间角问题
① 两条直线的夹角
两条直线夹角范围为:[0, 90°]
设直线L,m的方向向量分别为
a
,
b
则两直线夹角为:
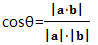
备注:
两条异面直线的夹角范围为(0, 90°],注意两条异面直线的夹角不会是0°
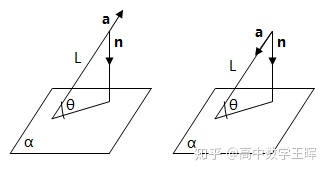
② 直线与平面的夹角
直线与平面夹角的范围:[0, 90°]
设直线L的方向向量为
a
,平面α的法向量为
n
直线L与平面α所成的角为:
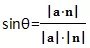
③ 二面角
二面角的范围:[0, 180°]
设平面α的法向量为
n1
,平面β的法向量为
n2
则平面α-L-β的二面角为法相量的夹角或者法相量夹角的补角。
如果是法相量的夹角:
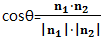
如果是法相量的夹角的补角:
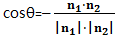
那么如何判断二面角是法相量的夹角还是法相量夹角的补角呢?
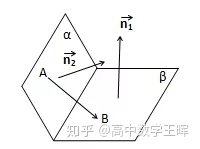
告诉大家一种判断的方法,在α内任意找一点A,β内找一点B,得到
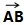
如果
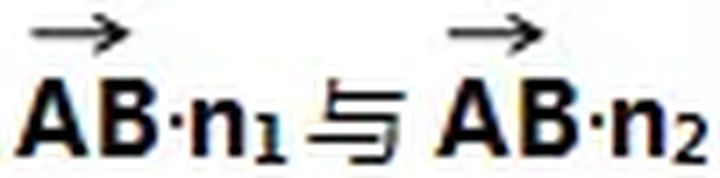
所得结果是同号,那么平面的二面角是两个法向量的夹角
如果
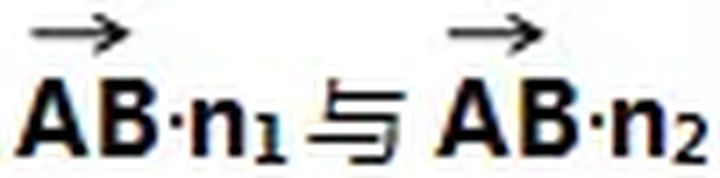
所得结果是异号,那么平面的二面角是两个法向量的夹角的补角
具体如下图: