博客

目录

SIoU loss Yolo版：

1简介

2SIoU Loss

2.1 Angle cost

2.2 Distance cost

2.3 Shape cost

2.4 IoU Cost

2.5 SIoU Loss

3实验结果

4参考

原版还没开源。

SIoU loss Yolo版：

车牌检测，有预训练模型

https://github.com/xialuxi/yolov5-car-plate

def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, SIoU=False, eps=1e-7):
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2

    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps

    iou = inter / union
    if GIoU or DIoU or CIoU:
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
        if SIoU:    # SIoU Loss https://arxiv.org/pdf/2205.12740.pdf
            s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5
            s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5
            sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)
            sin_alpha_1 = torch.abs(s_cw) / sigma
            sin_alpha_2 = torch.abs(s_ch) / sigma
            threshold = pow(2, 0.5) / 2
            sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
            # angle_cost = 1 - 2 * torch.pow( torch.sin(torch.arcsin(sin_alpha) - np.pi/4), 2)
            angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - np.pi / 2)
            rho_x = (s_cw / cw) ** 2
            rho_y = (s_ch / ch) ** 2
            gamma = angle_cost - 2
            distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)
            omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
            omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
            shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
            return iou - 0.5 * (distance_cost + shape_cost)
        if CIoU or DIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
                    (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center distance squared
            if DIoU:
                return iou - rho2 / c2  # DIoU
            elif CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha = v / (v - iou + (1 + eps))
                return iou - (rho2 / c2 + v * alpha)  # CIoU
        else:  # GIoU https://arxiv.org/pdf/1902.09630.pdf
            c_area = cw * ch + eps  # convex area
            return iou - (c_area - union) / c_area  # GIoU
    else:
        return iou  # IoU

目标检测是计算机视觉任务的核心问题之一，其有效性在很大程度上取决于损失函数的定义。传统的目标检测损失函数依赖于边界框回归指标的聚合，例如预测框和真实框（即

GIoU

、

CIoU

、

ICIoU

等）的距离、重叠区域和纵横比。

然而，迄今为止提出和使用的方法都没有考虑到所需真实框与预测框之间不匹配的方向。这种不足导致收敛速度较慢且效率较低，因为预测框可能在训练过程中“四处游荡”并最终产生更差的模型。

在本文中，提出了一种新的损失函数

SIoU

，其中考虑到所需回归之间的向量角度，重新定义了惩罚指标。应用于传统的神经网络和数据集，表明

SIoU

提高了训练的速度和推理的准确性。

在许多模拟和测试中揭示了所提出的损失函数的有效性。特别是，将

SIoU

应用于 COCO-train/COCO-val 与其他损失函数相比，提高了 +2.4% (mAP@0.5:0.95) 和 +3.6%(mAP@0.5)。

1简介

我们都知道目标检测中损失函数（

LF

）的定义起着重要作用。后者作为一种惩罚措施，需要在训练期间最小化，并且理想情况下可以将勾勒出目标的预测框与相应的真实框匹配。为目标检测问题定义

LF

有不同的方法，这些方法考虑到框的以下“不匹配”指标的某种组合：框中心之间的距离、重叠区域和纵横比。

最近 Rezatofighi 等人声称

Generalized IoU (GIoU) LF

优于其他标准

LF

的最先进的目标检测方法。虽然这些方法对训练过程和最终结果都产生了积极影响，但作者认为仍有很大改进的空间。因此，与用于计算图像中真实框和模型预测框不匹配的惩罚的传统指标并行——即距离、形状和

IoU

，本文作者建议还要考虑匹配的方向。这种添加极大地帮助了训练收敛过程和效果，因为它可以让预测框很快地移动到最近的轴，并且随后的方法只需要一个坐标 X 或 Y 的回归。简而言之，添加Angle惩罚成本有效地减少了损失的总自由度。

2SIoU Loss

SIoU损失函数由4个Cost函数组成：

• Angle cost

• Distance cost

• Shape cost

• IoU cost

2.1 Angle cost

添加这种角度感知 LF 组件背后的想法是最大限度地减少与距离相关的“奇妙”中的变量数量。基本上，模型将尝试首先将预测带到 X 或 Y 轴（以最接近者为准），然后沿着相关轴继续接近。

如果 𝛼 ≤Π/4，收敛过程将首先最小化𝛼 ， 否则最小化β：

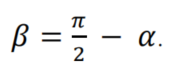
为了首先实现这一点，以以下方式引入和定义了LF组件：

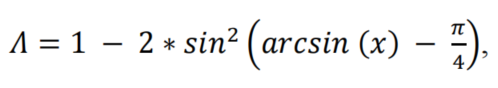
其中，


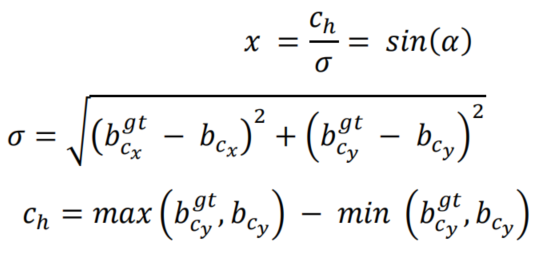
Angle cost

的曲线如图2所示。

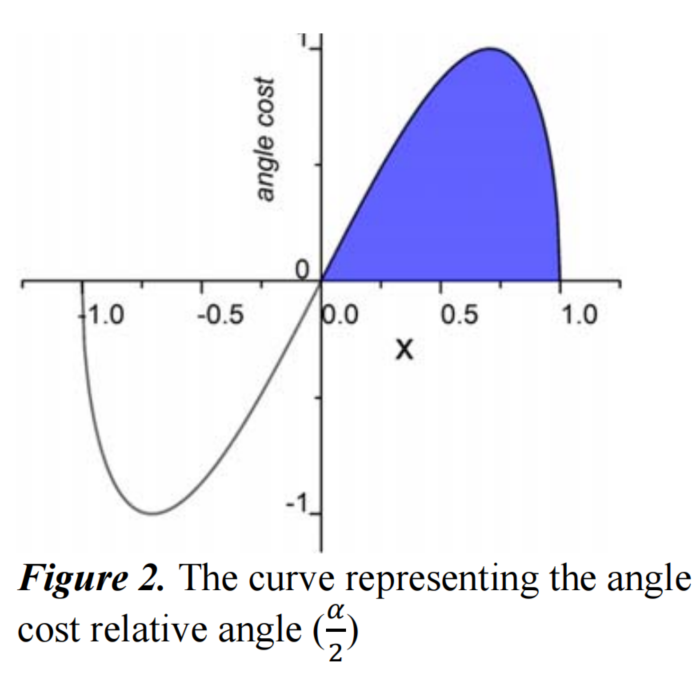
图2

2.2 Distance cost

考虑到上面定义的

Angle cost

，重新定义了

Distance cost

：

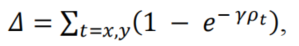
其中，

可以看出，当𝛼→0时，

Distance cost

的贡献大大降低。相反，𝛼越接近Π/4，

Distance cost

贡献越大。随着角度的增大，问题变得越来越难。因此，γ被赋予时间优先的距离值，随着角度的增加。

2.3 Shape cost


Shape cost

的定义为：

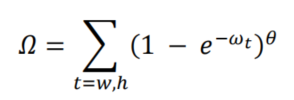
其中，

𝜃 的值定义了每个数据集的

Shape cost

及其值是唯一的。𝜃 的值是这个等式中非常重要的一项，它控制着对

Shape cost

的关注程度。如果 𝜃 的值设置为 1，它将立即优化一个Shape，从而损害Shape的自由移动。为了计算 𝜃 的值，作者将遗传算法用于每个数据集，实验上 𝜃 的值接近 4，文中作者为此参数定义的范围是 2 到 6。

2.4 IoU Cost


IoU cost

的定义为：

其中，

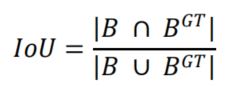
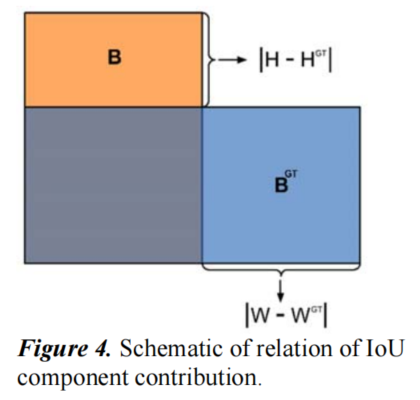
2.5 SIoU Loss

最后，回归损失函数为:

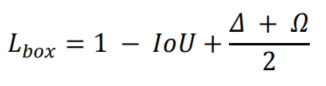
总损失函数为：

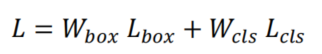
其中 是Focal Loss，、分别是框和分类损失权重。为了计算、、𝜃，使用了遗传算法。

3实验结果

图 10 总结了不同模型与 mAP@0.5:0.95 的推理时间。显然，Scylla-Net 的 mAP 值较高，而模型推理时间远低于比较模型的推理时间。

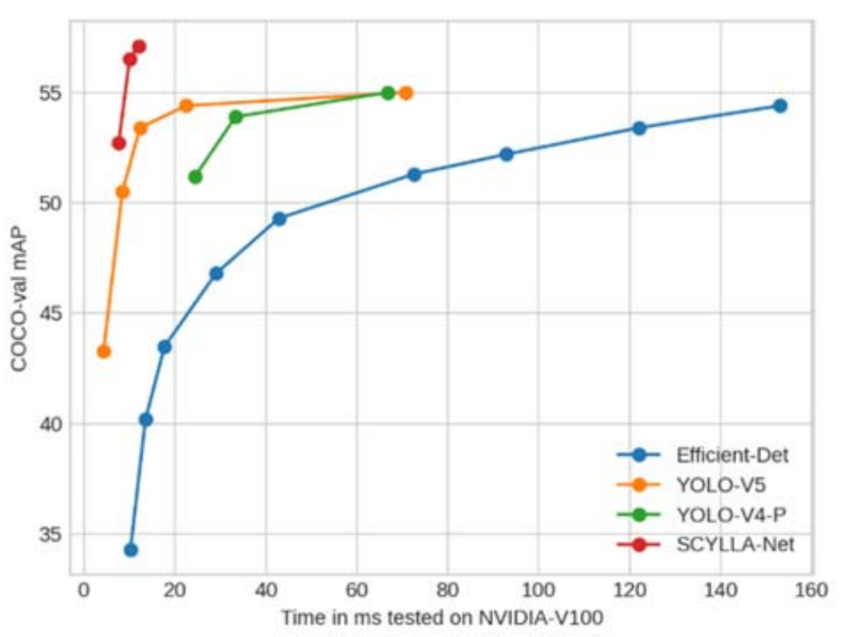
图 10

COCO-val 上

SIoU

的 mAP 为 52.7% mAP@0.5:0.95（包括预处理、推理和后处理为 7.6ms）和 70% mAP@0.5，同时

CIoU

为分别只有 50.3% 和 66.4%。

更大的模型可以达到 57.1% mAP@0.5:0.95（12ms 包括预处理、推理和后处理）和 74.3% mAP@0.5，而其他架构如

Efficient-Det-d7x

、

YOLO-V4

和

YOLO-V5

可以达到mAP@0.5:0.95分别为 54.4% (153ms)、47.1% (26.3ms) 和 50.4%（使用 fp16 进行 6.1ms）。

请注意，

YOLO-V5x6-TTA

在 COCO-val 上可以达到约 55%，但推理时间非常慢（FP16 时约为 72ms）。

4参考

[1].SIoU Loss: More Powerful Learning for Bounding Box Regression