离散推导
Spalding(1972)提出了混合差分格式,该格式结合了中心差分格式和迎风格式的优点。小Pe数情况下(
P
e
<
2
Pe<2
P
e
<
2
),使用中心差分格式,它具有二阶计算精度;大Pe数情况下(
P
e
>
2
Pe>2
P
e
>
2
),使用迎风格式计算控制体界面对流输运量并忽略扩散作用。虽然迎风格式只有一阶精度,但可较好的反应流动的输运特征。
混合差分格整合了中心差分格式和迎风格式的计算公式,使用分段线性的计算公式来近似通过网格边界面处的通量。通过左边界单位面积通量的混合差分格式计算公式为
q
w
=
F
w
[
1
2
(
1
+
2
P
e
w
)
ϕ
W
+
1
2
(
1
−
2
P
e
w
)
ϕ
P
]
,
−
2
<
P
e
w
<
2
q
w
=
F
w
ϕ
W
,
P
e
w
≥
2
q
w
=
F
w
ϕ
P
,
P
e
w
≤
−
2
}
(1)
\left. \begin{aligned} q_w &= F_w \left[ \frac{1}{2} \left( 1 + \frac{2}{Pe_w} \right) \phi_W +\frac{1}{2} \left( 1 – \frac{2}{Pe_w} \right) \phi_P \right] ,&-2<Pe_w<2\\ \\ q_w &=F_w \phi_W ,&Pe_w \ge2 \\ \\ q_w &= F_w \phi_P ,&Pe_w \le -2 \end{aligned} \right \}\tag{1}
q
w
q
w
q
w
=
F
w
[
2
1
(
1
+
P
e
w
2
)
ϕ
W
+
2
1
(
1
−
P
e
w
2
)
ϕ
P
]
,
=
F
w
ϕ
W
,
=
F
w
ϕ
P
,
−
2
<
P
e
w
<
2
P
e
w
≥
2
P
e
w
≤
−
2
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎫
(
1
)
公式(1)中,
P
e
w
Pe_w
P
e
w
是当地边界面处的Peclet数,例如左边界面处定义为
P
e
w
=
F
w
D
w
=
(
ρ
u
)
w
Γ
w
/
δ
x
W
P
(2)
Pe_w=\frac{F_w}{D_w}=\frac{(\rho u)_w}{\Gamma_w/\delta x_{WP}} \tag{2}
P
e
w
=
D
w
F
w
=
Γ
w
/
δ
x
W
P
(
ρ
u
)
w
(
2
)
q
w
q_w
q
w
指的是左边界处的总通量,包括对流和扩散,公式(1)第一个式子的推导如下,
F
e
ϕ
e
−
F
w
ϕ
w
=
D
e
(
ϕ
E
−
ϕ
P
)
−
D
w
(
ϕ
P
−
ϕ
W
)
⇒
[
F
e
ϕ
e
−
D
e
(
ϕ
E
−
ϕ
P
)
]
−
[
F
w
ϕ
w
−
D
w
(
ϕ
P
−
ϕ
W
)
]
=
0
⇒
q
e
−
q
w
=
0
(3)
\begin{aligned} &F_e \phi_e – F_w \phi_w = D_e(\phi_E-\phi_P) – D_w(\phi_P -\phi_W) \\ \\ \Rightarrow & [F_e \phi_e – D_e(\phi_E-\phi_P)]-[F_w \phi_w-D_w(\phi_P-\phi_W)] = 0\\ \\ \Rightarrow & q_e – q_w = 0 \end{aligned} \tag{3}
⇒
⇒
F
e
ϕ
e
−
F
w
ϕ
w
=
D
e
(
ϕ
E
−
ϕ
P
)
−
D
w
(
ϕ
P
−
ϕ
W
)
[
F
e
ϕ
e
−
D
e
(
ϕ
E
−
ϕ
P
)
]
−
[
F
w
ϕ
w
−
D
w
(
ϕ
P
−
ϕ
W
)
]
=
0
q
e
−
q
w
=
0
(
3
)
所以,在左边界处,当
∣
P
e
∣
<
2
|Pe|<2
∣
P
e
∣
<
2
时,对流项使用中心差分格式离散,即
ϕ
w
=
(
ϕ
W
+
ϕ
P
)
/
2
\phi_w=(\phi_W+\phi_P)/2
ϕ
w
=
(
ϕ
W
+
ϕ
P
)
/
2
。则左边界处通量有,
q
w
=
F
w
ϕ
w
−
D
w
(
ϕ
P
−
ϕ
W
)
=
F
w
(
ϕ
W
+
ϕ
P
2
)
−
D
w
(
ϕ
P
−
ϕ
W
)
=
(
F
w
2
+
D
w
)
ϕ
W
+
(
F
w
2
−
D
w
)
ϕ
P
=
F
w
[
1
2
(
1
+
2
P
e
w
)
ϕ
W
+
1
2
(
1
−
2
P
e
w
)
ϕ
P
]
(4)
\begin{aligned} q_w &=F_w \phi_w -D_w(\phi_P-\phi_W) \\ \\ &=F_w \left( \frac{\phi_W+\phi_P}{2} \right)-D_w(\phi_P-\phi_W) \\ \\ &=\left( \frac{F_w}{2}+D_w \right)\phi_W + \left( \frac{F_w}{2}-D_w \right)\phi_P \\ \\ &=F_w \left[\frac{1}{2} \left( 1+\frac{2}{Pe_w} \right)\phi_W +\frac{1}{2} \left( 1-\frac{2}{Pe_w} \right)\phi_P \right] \end{aligned} \tag{4}
q
w
=
F
w
ϕ
w
−
D
w
(
ϕ
P
−
ϕ
W
)
=
F
w
(
2
ϕ
W
+
ϕ
P
)
−
D
w
(
ϕ
P
−
ϕ
W
)
=
(
2
F
w
+
D
w
)
ϕ
W
+
(
2
F
w
−
D
w
)
ϕ
P
=
F
w
[
2
1
(
1
+
P
e
w
2
)
ϕ
W
+
2
1
(
1
−
P
e
w
2
)
ϕ
P
]
(
4
)
公式(1)中的后两个式子是省略了扩散项后的通量,并且对流项使用了迎风格式
q
w
=
F
w
ϕ
w
−
D
w
(
ϕ
P
−
ϕ
W
)
=
F
w
ϕ
w
=
F
w
ϕ
W
,
当
P
e
w
≥
2
=
F
w
ϕ
P
,
当
P
e
w
≤
−
2
(5)
\begin{aligned} q_w &= F_w\phi_w – D_w(\phi_P- \phi_W) \\ \\ &=F_w \phi_w\\ \\ &=F_w \phi_W ,当Pe_w \ge2 \\\\ &=F_w \phi_P ,当Pe_w \le-2 \end{aligned} \tag{5}
q
w
=
F
w
ϕ
w
−
D
w
(
ϕ
P
−
ϕ
W
)
=
F
w
ϕ
w
=
F
w
ϕ
W
,
当
P
e
w
≥
2
=
F
w
ϕ
P
,
当
P
e
w
≤
−
2
(
5
)
由公式(3)可知,对流扩散方程可以写成
q
e
−
q
w
=
0
(6)
q_e – q_w=0 \tag{6}
q
e
−
q
w
=
0
(
6
)
那么把混合离散格式(1)带入到离散方程(6),则
当
∣
P
e
∣
<
2
|Pe|<2
∣
P
e
∣
<
2
时,
q
e
−
q
w
=
F
e
[
1
2
(
1
+
2
P
e
e
)
ϕ
P
+
1
2
(
1
−
2
P
e
e
)
ϕ
E
]
−
F
w
[
1
2
(
1
+
2
P
e
w
)
ϕ
W
+
1
2
(
1
−
2
P
e
w
)
ϕ
P
]
=
0
(7)
\begin{aligned} q_e-q_w&=F_e \left[ \frac{1}{2} \left( 1+ \frac{2}{Pe_e} \right)\phi_P +\frac{1}{2} \left( 1- \frac{2}{Pe_e} \right) \phi_E \right] \\ \\ &\qquad -F_w \left[ \frac{1}{2} \left( 1+ \frac{2}{Pe_w} \right)\phi_W +\frac{1}{2} \left( 1- \frac{2}{Pe_w} \right) \phi_P \right] \\ \\ &=0 \end{aligned} \tag{7}
q
e
−
q
w
=
F
e
[
2
1
(
1
+
P
e
e
2
)
ϕ
P
+
2
1
(
1
−
P
e
e
2
)
ϕ
E
]
−
F
w
[
2
1
(
1
+
P
e
w
2
)
ϕ
W
+
2
1
(
1
−
P
e
w
2
)
ϕ
P
]
=
0
(
7
)
整理之,
[
F
e
2
(
1
+
2
P
e
e
)
−
F
w
2
(
1
−
2
P
e
w
)
]
ϕ
P
=
F
w
2
(
1
+
2
P
e
w
)
ϕ
W
−
F
e
2
(
1
−
2
P
e
e
)
ϕ
E
(8)
\begin{aligned} &\left[ \frac{F_e}{2}\left( 1+\frac{2}{Pe_e} \right)-\frac{F_w}{2}\left( 1-\frac{2}{Pe_w} \right) \right]\phi_P= \\ \\ &\qquad \qquad \qquad \frac{F_w}{2}\left( 1+\frac{2}{Pe_w} \right)\phi_W – \frac{F_e}{2} \left(1-\frac{2}{Pe_e} \right)\phi_E \end{aligned} \tag{8}
[
2
F
e
(
1
+
P
e
e
2
)
−
2
F
w
(
1
−
P
e
w
2
)
]
ϕ
P
=
2
F
w
(
1
+
P
e
w
2
)
ϕ
W
−
2
F
e
(
1
−
P
e
e
2
)
ϕ
E
(
8
)
因为
P
e
=
F
/
D
Pe=F/D
P
e
=
F
/
D
,带入上式并简化成熟悉的形式,
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
(9)
a_P \phi_P=a_W \phi_W + a_E \phi_E \tag{9}
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
(
9
)
系数为
a
W
=
F
w
2
(
1
+
2
P
e
w
)
=
F
w
2
(
1
+
2
F
w
/
D
w
)
=
D
w
+
F
w
2
(10)
\begin{aligned} a_W&=\frac{F_w}{2} \left( 1+\frac{2}{Pe_w} \right) \\ \\ &=\frac{F_w}{2} \left(1 + \frac{2}{F_w/D_w} \right) \\\\ &=D_w + \frac{F_w}{2} \end{aligned} \tag{10}
a
W
=
2
F
w
(
1
+
P
e
w
2
)
=
2
F
w
(
1
+
F
w
/
D
w
2
)
=
D
w
+
2
F
w
(
1
0
)
同理,
a
E
=
D
e
−
F
e
2
(11)
a_E=D_e-\frac{F_e}{2} \tag{11}
a
E
=
D
e
−
2
F
e
(
1
1
)
主系数,
a
P
=
(
D
e
+
F
e
2
)
+
(
D
w
−
F
w
2
)
=
(
D
e
−
F
e
2
+
F
e
)
+
(
D
w
+
F
w
2
−
F
w
)
=
(
D
e
−
F
e
2
)
+
(
D
w
+
F
w
2
)
+
(
F
e
−
F
w
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
(12)
\begin{aligned} a_P&=\left( D_e + \frac{F_e}{2} \right) +\left( D_w – \frac{F_w}{2} \right) \\ \\ &=\left( D_e – \frac{F_e}{2}+F_e \right) +\left( D_w + \frac{F_w}{2}-F_w \right) \\ \\ &=\left( D_e – \frac{F_e}{2} \right) +\left( D_w + \frac{F_w}{2} \right) + (F_e-F_w) \\ \\ &=a_W + a_E + (F_e-F_w) \end{aligned} \tag{12}
a
P
=
(
D
e
+
2
F
e
)
+
(
D
w
−
2
F
w
)
=
(
D
e
−
2
F
e
+
F
e
)
+
(
D
w
+
2
F
w
−
F
w
)
=
(
D
e
−
2
F
e
)
+
(
D
w
+
2
F
w
)
+
(
F
e
−
F
w
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
(
1
2
)
所以
∣
P
e
∣
<
2
|Pe|<2
∣
P
e
∣
<
2
时的系数为
a
W
=
D
w
+
F
w
2
a
E
=
D
e
−
F
e
2
a
P
=
a
W
+
a
E
+
(
F
e
−
F
w
)
}
(13)
\left. \begin{aligned} a_W &= D_w + \frac{F_w}{2} \\ \\ a_E &= D_e – \frac{F_e}{2} \\ \\ a_P &= a_W+ a_E + (F_e – F_w) \end{aligned} \right \} \tag{13}
a
W
a
E
a
P
=
D
w
+
2
F
w
=
D
e
−
2
F
e
=
a
W
+
a
E
+
(
F
e
−
F
w
)
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎫
(
1
3
)
当
P
e
≥
2
Pe \ge 2
P
e
≥
2
时,
q
e
−
q
w
=
F
e
ϕ
e
−
F
w
ϕ
w
=
F
e
ϕ
P
−
F
w
ϕ
W
=
0
⇒
F
e
ϕ
E
=
F
w
ϕ
W
(14)
\begin{aligned} q_e-q_w &= F_e \phi_e – F_w \phi_w \\ \\ &=F_e \phi_P – F_w \phi_W=0 \\ \\ \Rightarrow & F_e \phi_E=F_w\phi_W \end{aligned} \tag{14}
q
e
−
q
w
⇒
=
F
e
ϕ
e
−
F
w
ϕ
w
=
F
e
ϕ
P
−
F
w
ϕ
W
=
0
F
e
ϕ
E
=
F
w
ϕ
W
(
1
4
)
即,
a
W
=
F
w
,
a
E
=
0
a
P
=
F
e
=
F
w
+
(
F
e
−
F
w
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
}
(15)
\left. \begin{aligned} a_W=F_w,a_E=0 \\ \\ a_P = F_e = F_w + (F_e – F_w) \\ =a_W + a_E + (F_e- F_w) \end{aligned} \right \} \tag{15}
a
W
=
F
w
,
a
E
=
0
a
P
=
F
e
=
F
w
+
(
F
e
−
F
w
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
⎭
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎫
(
1
5
)
当
P
e
≤
−
2
Pe \le -2
P
e
≤
−
2
时,
q
e
−
q
w
=
F
e
ϕ
E
−
F
w
ϕ
P
=
0
⇒
−
F
w
ϕ
P
=
−
F
e
ϕ
E
(16)
\begin{aligned} &q_e – q_w = F_e \phi_E – F_w \phi_P = 0 \\ \\ \Rightarrow &-F_w \phi_P = -F_e \phi_E \end{aligned} \tag{16}
⇒
q
e
−
q
w
=
F
e
ϕ
E
−
F
w
ϕ
P
=
0
−
F
w
ϕ
P
=
−
F
e
ϕ
E
(
1
6
)
即,
a
E
=
−
F
e
,
a
W
=
0
a
P
=
−
F
w
=
−
F
e
+
(
F
e
−
F
w
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
}
(17)
\left. \begin{aligned} a_E = -F_e,a_W = 0 \\ \\ a_P=-F_w = -F_e + (F_e – F_w)\\ =a_W+a_E + (F_e-F_w) \end{aligned} \right \} \tag{17}
a
E
=
−
F
e
,
a
W
=
0
a
P
=
−
F
w
=
−
F
e
+
(
F
e
−
F
w
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
⎭
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎫
(
1
7
)
把系数公式(13)(15)(17)整合起来,
|
a w a_w a w |
a E a_E a E |
|
|---|---|---|
|
0 < P e < 2 0<Pe<2 0 < P e < 2 |
D w + F w / 2 > F w > 0 D_w+F_w/2 > F_w > 0 D w + F w / 2 > F w > 0 |
D e − F e / 2 > 0 > − F e D_e-F_e/2 > 0 > -F_e D e − F e / 2 > 0 > − F e |
|
− 2 < P e < 0 -2<Pe<0 − 2 < P e < 0 |
D w + F w / 2 > 0 > F w D_w+F_w/2>0>F_w D w + F w / 2 > 0 > F w |
D e − F e / 2 > − F e > 0 D_e-F_e/2>-F_e>0 D e − F e / 2 > − F e > 0 |
|
P e ≥ 2 Pe\ge2 P e ≥ 2 |
F w > D w + F w / 2 > 0 F_w>D_w+F_w/2>0 F w > D w + F w / 2 > 0 |
0 > D e − F e / 2 > − F e 0>D_e-F_e/2>-F_e 0 > D e − F e / 2 > − F e |
|
P e ≤ 2 Pe\le2 P e ≤ 2 |
0 > D w + F w / 2 > F w 0>D_w+F_w/2>F_w 0 > D w + F w / 2 > F w |
− F e > D e − F e / 2 > 0 -F_e>D_e-F_e/2>0 − F e > D e − F e / 2 > 0 |
所以混合差分格式离散一维对流扩散方程的系数为
a
W
=
m
a
x
[
F
w
,
D
w
+
F
w
2
,
0
]
a
E
=
m
a
x
[
−
F
e
,
D
e
−
F
e
2
,
0
]
a
P
=
a
W
+
a
E
+
(
F
e
−
F
w
)
}
(18)
\left. \begin{aligned} a_W=max\left[ F_w , D_w+\frac{F_w}{2},0\right] \\ \\ a_E=max\left[ -F_e, D_e-\frac{F_e}{2},0 \right] \\ \\ a_P=a_W +a_E + (F_e -F_w) \end{aligned}\quad \right \} \tag{18}
a
W
=
m
a
x
[
F
w
,
D
w
+
2
F
w
,
0
]
a
E
=
m
a
x
[
−
F
e
,
D
e
−
2
F
e
,
0
]
a
P
=
a
W
+
a
E
+
(
F
e
−
F
w
)
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎫
(
1
8
)
算例
用混合差分格式计算(
有限体积法(5)——对流-扩散方程的离散
)中算例的工况2,网格如下

该工况下有
u
=
2.5
m
/
s
,
F
=
F
e
=
F
w
=
ρ
u
=
2.5
,
D
=
D
e
=
D
w
=
Γ
/
δ
x
=
0.5
,
P
e
=
F
/
D
=
5
u=2.5m/s, \quad F=F_e=F_w=\rho u =2.5,\quad D=D_e=D_w=\Gamma / \delta x=0.5,\quad Pe=F/D=5
u
=
2
.
5
m
/
s
,
F
=
F
e
=
F
w
=
ρ
u
=
2
.
5
,
D
=
D
e
=
D
w
=
Γ
/
δ
x
=
0
.
5
,
P
e
=
F
/
D
=
5
,内部节点的离散可以套用公式(18)。
节点1:
∣
P
e
∣
<
2
|Pe|<2
∣
P
e
∣
<
2
时,有
F
e
(
ϕ
P
+
ϕ
E
2
)
−
F
A
ϕ
A
=
D
e
(
ϕ
E
−
ϕ
P
)
−
D
A
(
ϕ
P
−
ϕ
A
)
⇒
(
F
e
2
+
D
e
+
D
A
)
ϕ
P
=
(
D
e
−
F
e
2
)
ϕ
E
+
(
F
A
+
D
A
)
ϕ
A
⇒
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
(19)
\begin{aligned} &F_e \left( \frac{\phi_P+\phi_E}{2} \right)-F_A\phi_A=D_e(\phi_E-\phi_P) -D_A(\phi_P-\phi_A) \\ \\ \Rightarrow &\left( \frac{F_e}{2} + D_e +D_A \right) \phi_P=\left(D_e-\frac{F_e}{2} \right) \phi_E + \left(F_A + D_A \right)\phi_A \\ \\ \Rightarrow &a_P \phi_P = a_W\phi_W + a_E \phi_E + S_u \end{aligned} \tag{19}
⇒
⇒
F
e
(
2
ϕ
P
+
ϕ
E
)
−
F
A
ϕ
A
=
D
e
(
ϕ
E
−
ϕ
P
)
−
D
A
(
ϕ
P
−
ϕ
A
)
(
2
F
e
+
D
e
+
D
A
)
ϕ
P
=
(
D
e
−
2
F
e
)
ϕ
E
+
(
F
A
+
D
A
)
ϕ
A
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
(
1
9
)
系数,
a
W
=
0
a
E
=
D
e
−
F
e
/
2
S
u
=
(
F
A
+
D
A
)
ϕ
A
S
P
=
−
(
F
w
+
D
A
)
a
P
=
a
W
+
a
E
+
(
F
e
−
F
w
)
−
S
P
}
(20)
\left. \begin{aligned} a_W &=0 \\\\ a_E &= D_e – F_e/2\\\\ S_u &= (F_A +D_A)\phi_A \\ \\ S_P &=-(F_w + D_A) \\ \\ a_P &= a_W + a_E +(F_e-F_w) -S_P \end{aligned} \right \} \tag{20}
a
W
a
E
S
u
S
P
a
P
=
0
=
D
e
−
F
e
/
2
=
(
F
A
+
D
A
)
ϕ
A
=
−
(
F
w
+
D
A
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
−
S
P
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎫
(
2
0
)
P
e
≥
2
Pe\ge2
P
e
≥
2
时,有
F
e
ϕ
P
−
F
A
ϕ
A
=
0
−
D
A
(
ϕ
P
−
ϕ
A
)
⇒
(
F
e
+
D
A
)
ϕ
P
=
(
F
A
+
D
A
)
ϕ
A
⇒
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
(21)
\begin{aligned} & F_e \phi_P -F_A\phi_A=0-D_A(\phi_P-\phi_A) \\ \\ \Rightarrow &(F_e + D_A) \phi_P = (F_A+D_A) \phi_A \\ \\ \Rightarrow & a_P\phi_P = a_W\phi_W + a_E \phi_E +S_u \end{aligned} \tag{21}
⇒
⇒
F
e
ϕ
P
−
F
A
ϕ
A
=
0
−
D
A
(
ϕ
P
−
ϕ
A
)
(
F
e
+
D
A
)
ϕ
P
=
(
F
A
+
D
A
)
ϕ
A
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
(
2
1
)
系数,
a
W
=
a
E
=
0
S
u
=
(
F
A
+
D
A
)
ϕ
A
S
P
=
−
(
F
w
+
D
A
)
a
P
=
a
W
+
a
E
+
(
F
e
−
F
w
)
−
S
P
}
(22)
\left. \begin{aligned} a_W &=a_E=0 \\\\ S_u&=(F_A +D_A) \phi_A \\ \\ S_P&=-(F_w+D_A) \\ \\ a_P&=a_W + a_E + (F_e-F_w) -S_P \end{aligned} \right \} \tag{22}
a
W
S
u
S
P
a
P
=
a
E
=
0
=
(
F
A
+
D
A
)
ϕ
A
=
−
(
F
w
+
D
A
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
−
S
P
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎫
(
2
2
)
P
e
≤
−
2
Pe\le-2
P
e
≤
−
2
时,有
F
e
ϕ
E
−
F
A
ϕ
A
=
0
−
D
A
(
ϕ
P
−
ϕ
A
)
⇒
D
A
ϕ
P
=
−
F
e
ϕ
E
+
(
F
A
+
D
A
)
ϕ
A
⇒
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
(23)
\begin{aligned} &F_e \phi_E-F_A \phi_A=0-D_A(\phi_P-\phi_A) \\ \\ \Rightarrow &D_A \phi_P=-F_e\phi_E + (F_A+D_A)\phi_A \\\\ \Rightarrow &a_P \phi_P=a_W\phi_W + a_E \phi_E + S_u \end{aligned} \tag{23}
⇒
⇒
F
e
ϕ
E
−
F
A
ϕ
A
=
0
−
D
A
(
ϕ
P
−
ϕ
A
)
D
A
ϕ
P
=
−
F
e
ϕ
E
+
(
F
A
+
D
A
)
ϕ
A
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
(
2
3
)
系数,
a
W
=
0
a
E
=
−
F
e
S
u
=
(
F
A
+
D
A
)
ϕ
A
S
P
=
−
(
F
w
+
D
A
)
a
P
=
a
W
+
a
E
+
(
F
e
−
F
w
)
−
S
P
}
(24)
\left.\begin{aligned} a_W&=0 \\ \\ a_E &= -F_e\\ \\ S_u &= (F_A+D_A) \phi_A \\ \\ S_P &= -(F_w + D_A) \\ \\ a_P &= a_W + a_E + (F_e -F_w) – S_P \end{aligned} \right \} \tag{24}
a
W
a
E
S
u
S
P
a
P
=
0
=
−
F
e
=
(
F
A
+
D
A
)
ϕ
A
=
−
(
F
w
+
D
A
)
=
a
W
+
a
E
+
(
F
e
−
F
w
)
−
S
P
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎫
(
2
4
)
整合公式(20)、(22)和(24)有
|
a W a_W a W |
a E a_E a E |
S u S_u S u |
S P S_P S P |
|
|---|---|---|---|---|
|
∥ P e ∥ < 2 \|Pe\|<2 ∥ P e ∥ < 2 |
0 |
D e − F e / 2 D_e-F_e/2 D e − F e / 2 |
( F A + D A ) ϕ A (F_A+D_A)\phi_A ( F A + D A ) ϕ A |
− ( F w + D A ) -(F_w+D_A) − ( F w + D A ) |
|
P e ≥ 2 Pe\ge2 P e ≥ 2 |
0 | 0 |
( F A + D A ) ϕ A (F_A+D_A)\phi_A ( F A + D A ) ϕ A |
− ( F w + D A ) -(F_w+D_A) − ( F w + D A ) |
|
P e ≤ − 2 Pe\le-2 P e ≤ − 2 |
0 |
− F e -F_e − F e |
( F A + D A ) ϕ A (F_A+D_A)\phi_A ( F A + D A ) ϕ A |
− ( F w + D A ) -(F_w+D_A) − ( F w + D A ) |
所以节点1的离散方程为
{
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
a
W
=
0
a
E
=
m
a
x
[
−
F
e
,
(
D
e
−
F
e
2
)
,
0
]
S
u
=
(
F
A
+
D
A
)
ϕ
A
S
P
=
−
(
F
w
+
D
A
)
a
P
=
a
W
+
a
E
+
Δ
F
−
S
P
(25)
\left \{ \begin{aligned} a_P \phi_P &= a_W \phi_W + a_E\phi_E + S_u \\ \\ a_W &=0 \\\\ a_E &=max\left[ -F_e, \left(D_e-\frac{F_e}{2} \right), 0 \right]\\\\ S_u &=(F_A +D_A) \phi_A\\\\ S_P &=-(F_w+D_A) \\\\ a_P &=a_W + a_E +\Delta F -S_P \end{aligned} \right. \tag{25}
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎧
a
P
ϕ
P
a
W
a
E
S
u
S
P
a
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
=
0
=
m
a
x
[
−
F
e
,
(
D
e
−
2
F
e
)
,
0
]
=
(
F
A
+
D
A
)
ϕ
A
=
−
(
F
w
+
D
A
)
=
a
W
+
a
E
+
Δ
F
−
S
P
(
2
5
)
同理,节点5的离散方程为
{
a
P
ϕ
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
a
W
=
m
a
x
[
F
w
,
D
w
+
F
w
2
,
0
]
a
E
=
0
a
P
=
a
W
+
a
E
+
Δ
F
−
S
P
(26)
\left \{ \begin{aligned} a_P \phi_P &= a_W \phi_W + a_E\phi_E + S_u \\ \\ a_W&=max\left[ F_w , D_w+\frac{F_w}{2},0\right] \\ \\ a_E &=0 \\\\ a_P &=a_W + a_E +\Delta F -S_P \end{aligned} \right. \tag{26}
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎧
a
P
ϕ
P
a
W
a
E
a
P
=
a
W
ϕ
W
+
a
E
ϕ
E
+
S
u
=
m
a
x
[
F
w
,
D
w
+
2
F
w
,
0
]
=
0
=
a
W
+
a
E
+
Δ
F
−
S
P
(
2
6
)
|
S u S_u S u |
S P S_P S P |
|
|---|---|---|
|
P e ≥ 2 Pe \ge 2 P e ≥ 2 |
D B ϕ B D_B\phi_B D B ϕ B |
− D B -D_B − D B |
|
P e < 2 Pe < 2 P e < 2 |
( D B − F B ) ϕ B (D_B-F_B)\phi_B ( D B − F B ) ϕ B |
F B − D B F_B-D_B F B − D B |
上面的两个公式中,没有省略计算域边界的扩散项,还有
D
A
=
D
B
=
2
Γ
/
δ
x
=
2
D
,
F
A
=
F
B
=
F
D_A=D_B=2\Gamma/\delta x =2D, F_A=F_B=F
D
A
=
D
B
=
2
Γ
/
δ
x
=
2
D
,
F
A
=
F
B
=
F
。
那么本例中各节点的系数计算公式为
| 节点 |
a W a_W a W |
a E a_E a E |
S P S_P S P |
S u S_u S u |
|---|---|---|---|---|
| 1 | 0 | 0 |
− ( 2 D + F ) -(2D+F) − ( 2 D + F ) |
( 2 D + F ) ϕ A (2D+F)\phi_A ( 2 D + F ) ϕ A |
| 2,3,4 |
F F F |
0 | 0 | 0 |
| 5 |
F F F |
0 |
− 2 D -2D − 2 D |
2 D ϕ B 2D\phi_B 2 D ϕ B |
带入数值求解方程组,数值结果与解析解对比如下,可见
P
e
>
2
Pe>2
P
e
>
2
时混合差分格式对流项采用的就是迎风格式,所以两者结果基本一样;当
P
e
<
2
Pe<2
P
e
<
2
时,混合差分格式对流项采用的是中心差分格式,是二阶计算精度,所以比一阶计算精度的迎风格式要稍好一些。
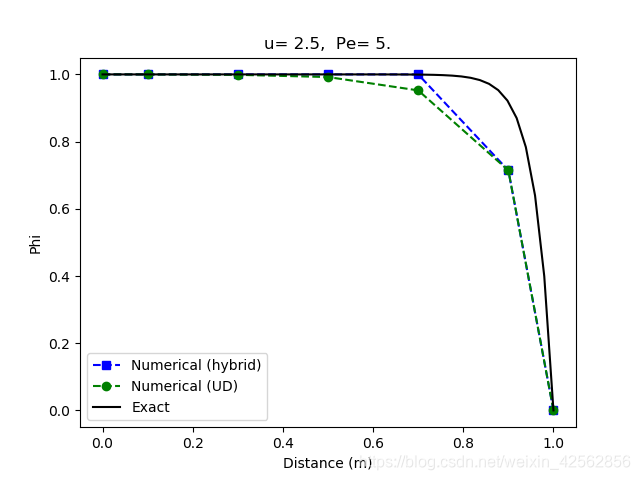
网格数为25的计算结果:
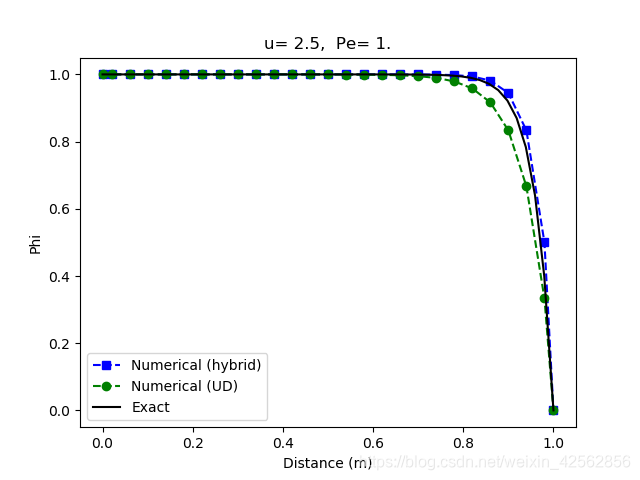
格式的特点
混合差分格式利用了中心差分格式和迎风格式的优点,在中心差分格式在高Pe数下不适用时切换到迎风格式,并将扩散项置零,这样可以减弱假扩散的影响。根据前面对中心差分和迎风格式的分析可知,混合格式是满足保守性的。从公式(18)可以看出,离散方程的系数永远是正值,所以也满足有界性的要求。Pe数较大时采用了迎风格式,所以保证了输运性。与高阶计算精度的QUICK格式相比,混合差分格式能够得到较为合理的数值解且具有较高的稳定性,因此该格式已被广泛应用于计算流体力学的工作中,在预测实际流动中有很大的作用。
混合差分格式的不足之处就是在
P
e
>
2
Pe>2
P
e
>
2
时采用的迎风格式只有一阶精度,为提高计算精度必须采用较密集的网格,但这样增加了计算成本。
计算程序
import numpy as np
import matplotlib.pyplot as plt
import math
#== parameters ===
nx = 25 # 网格单元数
nndoes = nx + 2 # 节点数,含边界
L = 1.0 # 长度,m
gamma = 0.1 #扩散系数 , kg/m.s
phi_a = 1 # 边界A的温度值
phi_b = 0 # 边界B的温度值
rho = 1.0 # 密度, kg/m^3
u = 2.5 # 速度,m/s # 0.1 , 2.5
# =========================
#== x grid ==
dx = L/nx # 网格间距
print('dx = ',dx)
x = np.zeros(nndoes) # x网格
x[1:nndoes-1] = np.linspace(dx/2, L-dx/2, nx) # 以边界A为原点创建网格点的坐标值
x[-1] = x[-2] + dx/2 #边界B的坐标值
print('x grid = ', x, '\n')
#== solution array ==
phi = np.zeros(nndoes) # 解向量
phi[0] = phi_a # 边界值
phi[-1] = phi_b
DD = gamma / dx # D
FF = rho * u # F
Pe = rho * u * dx / gamma # Peclet number
#== matrix ==
A = np.zeros((nx, nx))
b = np.zeros(nx)
#### 内部网格节点 #########
su = 0.0
sp = 0.0
for i in range(1, nx-1):
A[i][i-1] = -max(FF, DD+FF/2, 0)
A[i][i+1] = -max(-FF, DD-FF/2, 0)
A[i][i] = -(A[i][i-1] + A[i][i+1]) - sp
b[i] = su
# for boundary A
i = 0
A[i][i+1] = -max(-FF, 2*DD-FF/2, 0)
su = (2*DD + FF) * phi_a
sp = -(2*DD + FF)
A[i][i] = -A[i][i+1] - sp
b[i] = su
# for boundary B
i = nx-1
A[i][i-1] = -max(FF, DD+FF/2, 0)
if Pe>= 2:
su = 2*DD*phi_b
sp = -2*DD
else:
su = (2*DD - FF) * phi_b
sp = FF - 2*DD
A[i][i] = -A[i][i-1] - sp
b[i] = su
#==========================
print('A = \n', A, '\n')
print('b = \n', np.matrix(b).T ,'\n')
phi_temp = np.linalg.solve(A, b)
print('solution = \n', np.matrix(phi_temp).T, '\n')
phi[1:nndoes-1] = phi_temp
#===== for exact solution ======
xx = np.linspace(0, L, 50, endpoint=True)
exact_solution = np.zeros(50)
for i in range(50):
exact_solution[i] = (math.exp(rho*u*xx[i] / gamma) -1) / (math.exp(rho*u*L / gamma) -1) * (phi_b - phi_a) + phi_a
#UD_solution = np.array([1., 0.99984252, 0.99874016, 0.99212598, 0.95244094, 0.71433071, 0.])
UD_solution = np.array([1.0, 0.9999999867545231, 0.9999999470180921, 0.9999998675452304, 0.999999708599507,
0.9999993907080597, 0.9999987549251652, 0.9999974833593763, 0.9999949402277984, 0.9999898539646429,
0.9999796814383317, 0.9999593363857093, 0.9999186462804649, 0.9998372660699758, 0.9996745056489976,
0.9993489848070412, 0.9986979431231279, 0.9973958597553012, 0.9947916930196478, 0.9895833595483406,
0.9791666926057266, 0.9583333587204984, 0.9166666909500418, 0.8333333554091289, 0.6666666843273031,
0.3333333421636515, 0.0])
plt.xlabel('Distance (m)')
plt.ylabel('Phi')
plt.plot(x,phi ,'bs--', label='Numerical (hybrid)')
plt.plot(x,UD_solution ,'go--', label='Numerical (UD)')
plt.plot(xx,exact_solution,'k', label='Exact')
title = 'u= '+str(u)+', Pe= %.3f'% Pe
plt.title(title.rstrip('0'))
plt.legend()
plt.show()
参考资料
Versteeg H K , Malalasekera W . An introduction to computational fluid dynamics : the finite volume method = 计算流体动力学导论[M]. 世界图书出版公司, 2010.